雖然在WPF中可以使用TranslateTransform、RotateTransform、ScaleTransform等進行幾何變換,但我們也可以使用更底層的MatrixTransform(矩陣變換)來進行更復雜的復合變換。
首先我們矩陣如何影響幾何變換的:
1,縮放操作
觀察下面的矩陣乘法
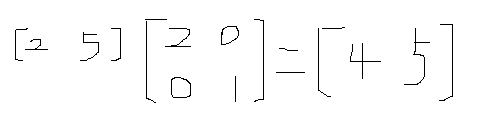
如果我們用[2 5]代表點(2,5),我們發現其乘以一個矩陣後變成了[4,5],與之對應的點是(4,5),這相當與其X坐標變成了原來的兩倍。
同理:
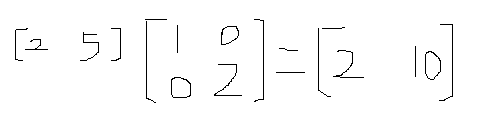
經過矩陣乘法後點(2,5)的Y坐標變成了原來的兩倍(2,10)。
我們可以總結出這樣的結論:
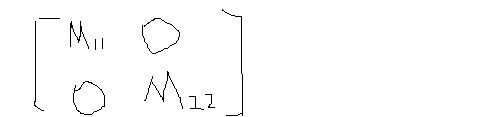
可以將矩陣的第二和第三個元素設置為0並用矩陣中M11和M22來進行縮放操作,其中M11是對X坐標進行縮放,M22是對Y坐標進行縮放
2,旋轉操作
觀察下面的矩陣乘法:
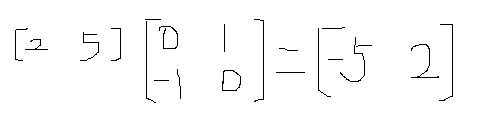
向量(-5,2)相當於是向量(2,5)按照順時針方向旋轉了90度。
但這裡並沒有總結出向縮放一樣的簡單結論,但我們可以知道,我們可以使用如下的2X2矩陣:
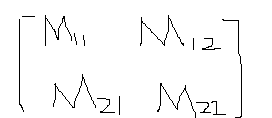
來對點進行線性變換(旋轉,縮放。注意:平移變換不是線性變換),即將點對應的矩陣乘以該線性變換矩陣便可。
3,平移操作
在矩陣加法中:
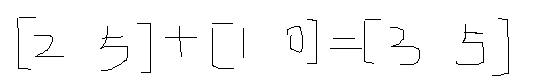
我們可以發現點(3,5)實際是在點(2,5)的基礎上想X方向平移1一個單位。
同理,
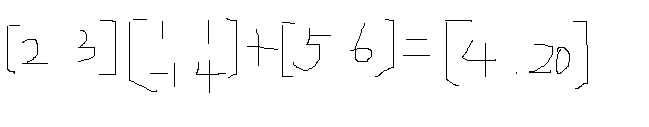
點(2,6)實際是在點(2,5)的基礎上想Y方向平移1一個單位。
我們可以得到如下結論:
我們可以使用點對應的矩陣加上如下的矩陣

來實現平移操作,其中offsetX實現了X軸方向上的平移,offsetY實現了Y方向上的平移。
4,幾種操作的融合
如果僅僅是簡單的單一操作(僅旋轉或僅平移等)我們就沒有必要在這裡進行討論了。現在我們需要將幾種幾何變換揉合在一起,比如平移對象的同時旋轉對象等,我們可以將矩陣乘法與加法揉合在一起進行混合運算。比如向量(2,3)先進行縮放和旋轉後再分別在X與Y軸方向上平移了5個與6個單位
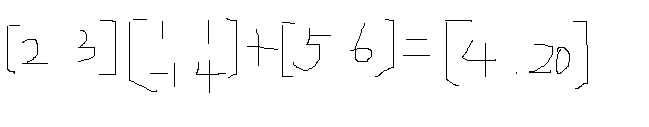
上面的這種變換稱為仿射變換(affine transformation)
注意:這種幾何變換在操作的先後順序上是需要注意的,不同的操作次序可以帶來不同的結果,比如上面的例子,如果我們先進行平移操作後進行縮放與旋轉將得到如下結果:
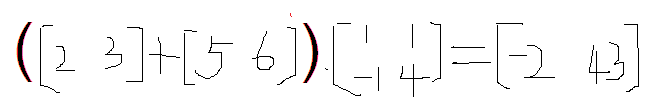
其實我們更希望將仿射變換中的幾個矩陣存儲到一個矩陣中來,一種較好的方式是將變換用到的2X2矩陣變成3X3矩陣,這也就是為什麼我們WPF中的變換矩陣是3X3的。
在如下矩陣中:
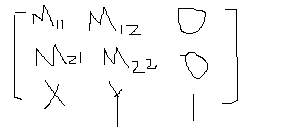
其中M11,M12,M21,M22就來自於線性變換矩陣,用於指示旋轉縮放等線性變換;X, Y來自與平移矩陣,用於指示平移變換。
由於最右邊一列始終是001,所以WPF中的MatrixTransform類的構造函數僅僅需要指定6個參數。