類-誰能幫我看下下面這段代碼，多項式乘法和+=操作運行不了，求助啊，到底錯在哪了

誰能幫我看下下面這段代碼，多項式乘法和+=操作運行不了，求助啊，到底錯在哪了

#include
#include
using namespace std;
class Polynomial
{
double *p_coefs;
int *p_exps, num;
public:
Polynomial();
Polynomial(double coefs[], int exps[], int size);//系數數組、指數數組和項數
Polynomial(const Polynomial&x);
~Polynomial();
//賦值操作符
Polynomial &operator=(const Polynomial&x)
{
if (&x == this) return *this;
num = x.num;
delete[]p_coefs;
delete[]p_exps;
p_coefs = new double[x.num];
p_exps = new int[x.num];
for (int i = 0; i <x. num; i++) { p_coefs[i] = x.p_coefs[i]; }
for (int j = 0; j <x.num; j++) { p_exps[j] = x.p_exps[j]; }
return *this;
}
//最高冪指數
int degree()const
{
return p_exps[num - 1];
}
//計算多項式的值
double evaluate(double x) const
{
double value = 0, temp = x;
for (int i = 0; i < num; i++)
{
for (int j = 0; j < p_exps[i]; j++) x *= temp;
x *= p_coefs[i];
value += x;
x = temp;
}
return value;
}
//判斷兩多項式是否相等
bool operator==(const Polynomial&x)const
{
if (num != x.num)return false;
for (int i = 0; i < num; i++)
if (p_exps[i] != x.p_exps[i] || p_coefs[i] != x.p_coefs[i])return false;
return true;
}
//判斷兩多項式是否不相等
bool operator!=(const Polynomial&x)const
{
if (num != x.num) return true;
for (int i = 0; i < num; i++)
if (p_exps[i] != x.p_exps[i] || p_coefs[i] != x.p_coefs[i])return true;
return false;

}
//多項式的加法
Polynomial operator+(const Polynomial&x)const
{
    Polynomial new_poly;
    new_poly.num = num + x.num;
    new_poly.p_coefs = new double[num +x.num];
    new_poly.p_exps = new int[num + x.num];
    for (int i = 0; i < num; i++) { new_poly.p_coefs[i] = p_coefs[i]; }
    for (int j = 0; j < num; j++) { new_poly.p_exps[j] = p_exps[j]; }
    for (int i = num; i <new_poly.num; i++) { new_poly.p_coefs[i] = x.p_coefs[i - num]; }
    for (int j = num; j <new_poly.num; j++) { new_poly.p_exps[j] = x.p_exps[j - num]; }
    for (int i = 0; i < new_poly.num; i++)
        for (int j = i + 1; j < new_poly.num; j++)
        {
            if (new_poly.p_exps[i] == new_poly.p_exps[j])
            {
                new_poly.p_coefs[i] = new_poly.p_coefs[i] + new_poly.p_coefs[j];
                new_poly.p_coefs[j] = 0;
            }
        }
    return new_poly;
}
//多項式的減法
Polynomial operator-(const Polynomial&x)const
{
    Polynomial poly,poly1;
    poly.num = num ;
    poly.p_coefs = new double[num];
    poly.p_exps = new int[num];
    for (int i = 0; i < x.num; i++) { poly.p_coefs[i] =p_coefs[i]; }
    for (int j = 0; j < x.num; j++) { poly.p_exps[j] = p_exps[j]; }
    poly1.num = x.num;
    poly1.p_coefs = new double[x.num];
    poly1.p_exps = new int[x.num];
    for (int i = 0; i < x.num; i++) { poly1.p_coefs[i] = -x.p_coefs[i]; }
    for (int j = 0; j < x.num; j++) { poly1.p_exps[j] = x.p_exps[j]; }
    return poly+poly1;
}
//多項式的乘法
Polynomial operator*(const Polynomial&x)const
{
    Polynomial *p,sum;
    p = new Polynomial[num];
     for (int i = 0; i < num;i++)
    { 
        for (int j = 0; j < x.num; j++)
        {
            p[i].p_coefs[j] = p_coefs[i] * x.p_coefs[j];
            p[i].p_exps[j] = p_exps[i] + x.p_exps[j];

        }

     }
     for (int i = 0; i < num; i++) {
         sum =sum+p[i];
     }
    return sum;

}
//多項式的加法
Polynomial& operator+=(const Polynomial&x)
{
    {return *this+ x; }
}
//多項式的減法
Polynomial& operator-=(const Polynomial&x)
{return *this - x;}
Polynomial& operator*=(const Polynomial&x)
{
    return *this * x;
}
void display()const;

};
//下面兩個重載函數實現構造函數
Polynomial::Polynomial()
{
p_coefs = NULL; p_exps = NULL;
num = 0;
}
Polynomial::Polynomial(double coefs[], int exps[], int size)
{
num = size;
p_coefs = new double[num];
p_exps = new int[num];
for (int i = 0; i < num; i++) { p_coefs[i] = coefs[i]; }
for (int j = 0; j < num; j++) { p_exps[j] = exps[j]; }
}
Polynomial::Polynomial(const Polynomial&x)
{

num = x.num;
p_coefs = new double[num];
p_exps = new int[num];
for (int i = 0; i < num; i++) { p_coefs[i] = x.p_coefs[i]; }
for (int j = 0; j < num; j++) { p_exps[j] = x.p_exps[j]; }

}
//析構函數
Polynomial::~Polynomial()
{
delete[]p_coefs;
p_coefs = NULL;
delete[]p_exps;
p_exps = NULL;
num = 0;
}

//顯示多項式
void Polynomial::display()const
{
double t1;
int t2;
//冒泡排序
for (int j = 0; j < num - 1; j++)
for (int i = 0; i < num - 1 - j; i++)
if (p_exps[i]>p_exps[i + 1])
{
t1 = p_coefs[i]; t2 = p_exps[i];
p_coefs[i] = p_coefs[i + 1]; p_exps[i] = p_exps[i + 1];
p_coefs[i + 1] = t1; p_exps[i + 1] = t2;
}
if (p_coefs[0] != 0)
{
if (p_exps[0] != 0 && p_exps[0] != 1)
{
if (p_coefs[0] != 1 && p_coefs[0] != -1)cout << p_coefs[0] << "x^" << p_exps[0];
else if (p_coefs[0] == 1)cout << "x^" << p_exps[0];
else cout << "-x^" << p_exps[0];
}
else if (p_exps[0] == 0)
{
cout << p_coefs[0];
}
else
{
if (p_coefs[0] != 1 && p_coefs[0] != -1)cout << p_coefs[0] << "x";
else if (p_coefs[0] == 1)cout << "x";
else cout << "-x";
}

}
for (int i = 1; i < num; i++)
{
    if (p_coefs[i] != 0)
    {
        if (p_exps[i] != 0 && p_exps[i] != 1)
        {
            if (p_coefs[i] > 0 && p_coefs[i] != 1 && p_coefs[i] != -1)cout << '+' << p_coefs[i] << "x^" << p_exps[i];
            else if (p_coefs[i] == 1)cout << "+x^" << p_exps[i];
            else if (p_coefs[i] == -1)cout << "-x^" << p_exps[i];
            else cout << p_coefs[i] << "x^" << p_exps[i];
        }
        else if (p_exps[i] == 0)
        {
            cout << p_coefs[i];
        }
        else
        {
            if (p_coefs[i] != 1 && p_coefs[i] != -1)cout << p_coefs[i] << "x";
            else if (p_coefs[i] == 1)cout << "x";
            else cout << "-x";
        }

    }
}
cout << endl;

}
int main()
{
double a[5] = { 1,2,3,4,5 }, i[5] = { 1,3,5,7,10 };
int c = 5, b[5] = { 1,2,3,4,5 }, j[5] = { 1,3,5,8,7 };
Polynomial poly1(a, b, c), poly2, poly3(i, j, c),poly4,poly5;
cout << "多項式一:"; poly1.display();
poly2 = poly1;
cout << "多項式二:"; poly2.display();
cout << "多項式三:"; poly3.display();
cout <<"多項式一最高次冪:"<< poly1.degree() << endl;
cout << "多項式一值為:" << poly1.evaluate(3) << endl;
cout <<"多項式二與三是否相等:"<< boolalpha << (poly2 == poly3) << endl;
cout << "多項式二與三是否不相等:" << boolalpha << (poly2 != poly3) << endl;
cout << "多項式一與三的和:"; (poly1 + poly3).display();
cout << "多項式一與三的差:"; (poly1 - poly3).display();
cout << "多項式一與三的積:"; (poly1 * poly3).display();
poly2 += poly3;
cout << "多項式二增加後:"; poly2.display();
poly2 -= poly3;
cout << "多項式二減少後:"; poly2.display();
poly2 *= poly3;
cout << "多項式二相乘後:"; poly2.display();
system("pause");
return 0;
}

最佳回答：

多項式乘法中，樓主光new Polynomial[num]是不夠的 ，還需要為裡面的double數組，int數組也都需要new，num也要賦值
加的三句我加注釋了

 //多項式的乘法
    Polynomial operator*(const Polynomial&x)const
    {
        Polynomial *p,sum;
        p = new Polynomial[num];
        for (int i = 0; i < num;i++)
        { 
            p[i].p_coefs = new double[x.num]; //要new
            p[i].p_exps = new int[x.num];        //要new
            p[i].num = x.num;                       //num也要賦值
            for (int j = 0; j < x.num; j++)
            {
                p[i].p_coefs[j] = p_coefs[i] * x.p_coefs[j];
                p[i].p_exps[j] = p_exps[i] + x.p_exps[j];
            }

        }
        for (int i = 0; i < num; i++) {
            sum =sum+p[i];
        }
        return sum;
    }

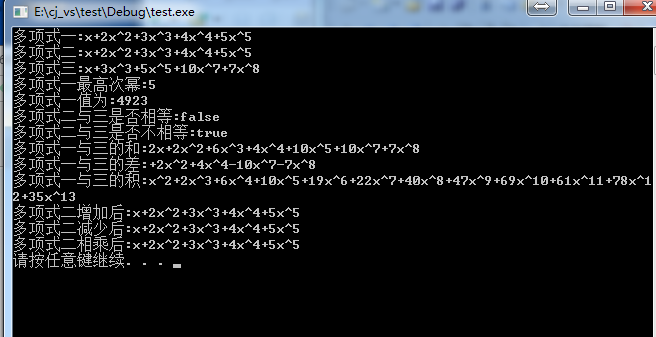
結果：