題目描述: 目前我有一個正方體,邊長為N,我以單位1為邊長,將正方體分割成N*N*N個單位正方體,請問裡面有多少對正方體公共點不大於2?
當N=1,有0對,當N=2,有16對,當N=3,有297對,給出關於N的公式。
題主關於第一個第二個第三個的答案是正確的,注意公共點不大於2,也就是說公共點允許0、1、2這三種情況,根據實際情況其實只需要滿足方塊之間沒有公共面即可滿足條件。
所以,下面給出我的推論過程:
N=1,顯然,0對
N=2,形狀如下圖(丑點忍著看吧,ps純手工畫的)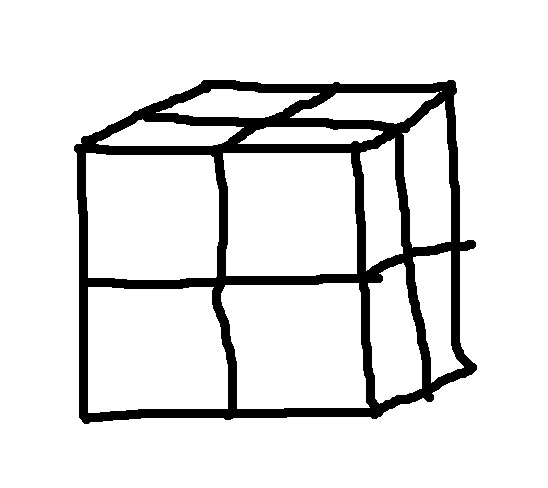
可以看到,由8個角上的小方塊組成,那麼我們開始數面,對於每個小方塊來說,與其他小方塊連接的面均是3,那麼我們任意選定一個小方塊,將該小方塊和與該小方塊面相接觸的小方塊排除的話,那麼我們就會剩下2*2*2-(3 + 1)=4 也就是4個小方塊,也就是說,剩下四個小方塊與所選定的小方塊之間是滿足公共點不大於2的條件的,那麼對於8各小方塊,我們總共就有,4*8=32種,排除重復的(以A方塊為基准的時候選擇到了B方塊,以B方塊為基准的時候選擇到了A方塊,但是實際上,兩個只能算一對)要除以2,所以,最終結果是 32/2=16
N=3,形狀如下圖(還是依舊那麼丑)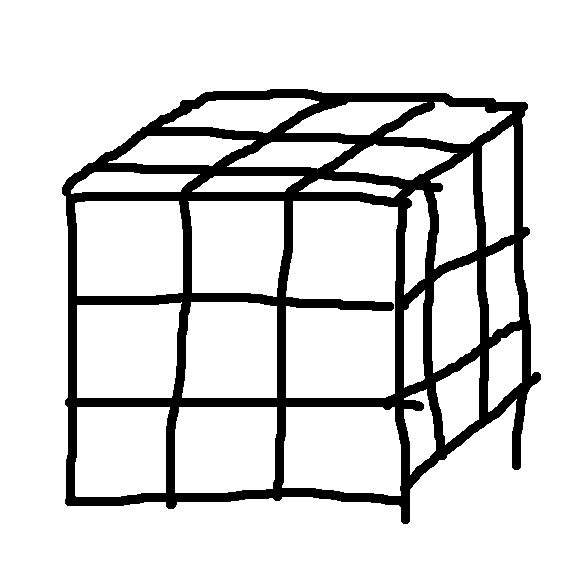
這種情況比較有意思,可以按照鄰接的面的數量分成四類小方塊,
第一類:8個角上的,有8個小方塊,每個小方塊鄰接的面數為3,也就是說,這類小方塊將會挖走4個小方塊(自己一個,鄰接的三個),剩下的與它全部滿足條件,按照總數為3^3=27的話,那麼滿足條件的小方塊為 27-4=23個,好的,這個結果先放著
第二類:12條邊上的,有12個小方塊,每個小方塊鄰接的面數為4,這類小方塊將會挖走5個小方塊(自己一個,鄰接的四個),剩下的與它全部滿足條件,那麼滿足條件的小方塊為 27-5=22個,這個結果也放著
第三類:6個面心(在外面能看到的不屬於邊也不屬於角上的),共6個,每個小方塊鄰接的面數為5,這類小方塊將會挖走6個小方塊,同理滿足條件的小方塊數為 27-6=21個
第四類:中心處(其實就是在外面看不到的小方塊),共1個,每個小方塊鄰接的面數為6,這類小方塊將會挖走7個小方塊,與之滿足條件的小方塊個數為27-7=20個。
好的,有了這四類小方塊,對應的個數以及每類小方塊所挖走的方塊的數量之後,那麼我們就可以按照N=2時候的思路,列出如下的式子:
(8*23 + 12*22+6*21+20)/2=297
式子可以整理一下:
(8*(3^3-4)+12*1*(3^3-5)+6*(1^2)*(3^3-6)+(1^3)*(3^3-7))/2=297
N=4,我就不畫圖了,大家可以腦洞一下。
這種情況下,小方塊實際上還是分為4類,這4類和在N=3的時候給出的一樣,但是這個數量不一樣,我直接給出各個類對應的數量:
第一類:8個角,8個小方塊
第二類:12條邊,每邊2個小方塊,所以12*2 = 24個
第三類:6個面,每面4個,所以 6 * (2^2)=24 個
第四類:4*4*4-8-24 - 24 = 8 個,排除法嘛,其實就是 (2^3)=8 個,
所以嘛,和N=3的時候也一樣,列出的式子就是:
(8*(4^3-4)+12*2*(4^3-5)+6*(2^2)*(4^3-6)+(2^3)*(4^3-7))/2=1 872
N=5類推。。。。。
所以歸類就出來了:
N=1 滿足條件的對數為:0
N>1 滿足條件的對數為:(8*(N^3-4)+12*(N-2)*(N^3-5)+6*((N-2)^2)*(N^3-6)+(N-2)^3*(N^3-7))/2


