C通過運行時堆棧支持遞歸函數的實現。遞歸函數就是直接或間接調用自身的函數。
許多教科書都把計算機階乘和菲波那契數列用來說明遞歸,非常不幸我們可愛的著名的老潭老師的《C語言程序設計》一書中就是從階乘的計算開始的函數遞歸。導 致讀過這本經書的同學們,看到階乘計算第一個想法就是遞歸。但是在階乘的計算裡,遞歸並沒有提供任何優越之處。在菲波那契數列中,它的效率更是低的非常恐 怖。
這裡有一個簡單的程序,可用於說明遞歸。程序的目的是把一個整數從二進制形式轉換為可打印的字符形式。例如:給出一個值4267,我們需要依次產生字符‘4’,‘2’,‘6’,和‘7’。就如在printf函數中使用了%d格式碼,它就會執行類似處理。
我們采用的策略是把這個值反復除以10,並打印各個余數。例如,4267除10的余數是7,但是我們不能直接打印這個余數。我們需要打印的是機器字符集中 表示數字‘7’的值。在ASCII碼中,字符‘7’的值是55,所以我們需要在余數上加上48來獲得正確的字符,但是,使用字符常量而不是整型常量可以提 高程序的可移植性。‘0’的ASCII碼是48,所以我們用余數加上‘0’,所以有下面的關系:
‘0’+ 0 =‘0’
‘0’+ 1 =‘1’
‘0’+ 2 =‘2’
...
從這些關系中,我們很容易看出在余數上加上‘0’就可以產生對應字符的代碼。接著就打印出余數。下一步再取商的值,4267/10等於426。然後用這個值重復上述步驟。
這種處理方法存在的唯一問題是它產生的數字次序正好相反,它們是逆向打印的。所以在我們的程序中使用遞歸來修正這個問題。
我們這個程序中的函數是遞歸性質的,因為它包含了一個對自身的調用。乍一看,函數似乎永遠不會終止。當函數調用時,它將調用自身,第2次調用還將調用自身,以此類推,似乎永遠調用下去。這也是我們在剛接觸遞歸時最想不明白的事情。但是,事實上並不會出現這種情況。
這個程序的遞歸實現了某種類型的螺旋狀while循環。while循環在循環體每次執行時必須取得某種進展,逐步迫近循環終止條件。遞歸函數也是如此,它在每次遞歸調用後必須越來越接近某種限制條件。當遞歸函數符合這個限制條件時,它便不在調用自身。
在程序中,遞歸函數的限制條件就是變量quotient為零。在每次遞歸調用之前,我們都把quotient除以10,所以每遞歸調用一次,它的值就越來越接近零。當它最終變成零時,遞歸便告終止。
/*接受一個整型值(無符號0,把它轉換為字符並打印它,前導零被刪除*/
#include <stdio.h>
int binary_to_ascii( unsigned int value)
{
unsigned int quotient;
quotient = value / 10;
if( quotient != 0)
binary_to_ascii( quotient);
putchar ( value % 10 + '0' );
}
遞歸是如何幫助我們以正確的順序打印這些字符呢?下面是這個函數的工作流程。
1. 將參數值除以10
2. 如果quotient的值為非零,調用binary-to-ascii打印quotient當前值的各位數字
3. 接著,打印步驟1中除法運算的余數
注意在第2個步驟中,我們需要打印的是quotient當前值的各位數字。我們所面臨的問題和最初的問題完全相同,只是變量quotient的 值變小了。我們用剛剛編寫的函數(把整數轉換為各個數字字符並打印出來)來解決這個問題。由於quotient的值越來越小,所以遞歸最終會終止。
一旦你理解了遞歸,閱讀遞歸函數最容易的方法不是糾纏於它的執行過程,而是相信遞歸函數會順利完成它的任務。如果你的每個步驟正確無誤,你的限制條件設置正確,並且每次調用之後更接近限制條件,遞歸函數總是能正確的完成任務。
但是,為了理解遞歸的工作原理,你需要追蹤遞歸調用的執行過程,所以讓我們來進行這項工作。追蹤一個遞歸函數的執行過程的關鍵是理解函數中所聲 明的變量是如何存儲的。當函數被調用時,它的變量的空間是創建於運行時堆棧上的。以前調用的函數的變量扔保留在堆棧上,但他們被新函數的變量所掩蓋,因此 是不能被訪問的。
當遞歸函數調用自身時,情況於是如此。每進行一次新的調用,都將創建一批變量,他們將掩蓋遞歸函數前一次調用所創建的變量。當我追蹤一個遞歸函數的執行過程時,必須把分數不同次調用的變量區分開來,以避免混淆。
程序中的函數有兩個變量:參數value和局部變量quotient。下面的一些圖顯示了堆棧的狀態,當前可以訪問的變量位於棧頂。所有其他調用的變量飾以灰色的陰影,表示他們不能被當前正在執行的函數訪問。
假定我們以4267這個值調用遞歸函數。當函數剛開始執行時,堆棧的內容如下圖所示:

執行除法之後,堆棧的內容如下:

接著,if語句判斷出quotient的值非零,所以對該函數執行遞歸調用。當這個函數第二次被調用之初,堆棧的內容如下:
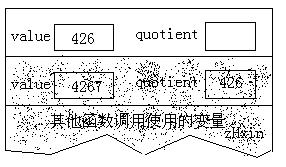
堆棧上創建了一批新的變量,隱藏了前面的那批變量,除非當前這次遞歸調用返回,否則他們是不能被訪問的。再次執行除法運算之後,堆棧的內容如下:

quotient的值現在為42,仍然非零,所以需要繼續執行遞歸調用,並再創建一批變量。在執行完這次調用的出發運算之後,堆棧的內容如下:

此時,quotient的值還是非零,仍然需要執行遞歸調用。在執行除法運算之後,堆棧的內容如下:
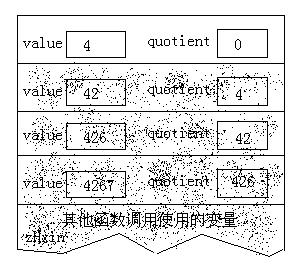
不算遞歸調用語句本身,到目前為止所執行的語句只是除法運算以及對quotient的值進行測試。由於遞歸調用這些語句重復執行,所以它的效果 類似循環:當quotient的值非零時,把它的值作為初始值重新開始循環。但是,遞歸調用將會保存一些信息(這點與循環不同),也就好是保存在堆棧中的 變量值。這些信息很快就會變得非常重要。
現在quotient的值變成了零,遞歸函數便不再調用自身,而是開始打印輸出。然後函數返回,並開始銷毀堆棧上的變量值。
每次調用putchar得到變量value的最後一個數字,方法是對value進行模10取余運算,其結果是一個0到9之間的整數。把它與字符常量‘0’相加,其結果便是對應於這個數字的ASCII字符,然後把這個字符打印出來。
輸出4:

接著函數返回,它的變量從堆棧中銷毀。接著,遞歸函數的前一次調用重新繼續執行,她所使用的是自己的變量,他們現在位於堆棧的頂部。因為它的value值是42,所以調用putchar後打印出來的數字是2。

接著遞歸函數的這次調用也返回,它的變量也被銷毀,此時位於堆棧頂部的是遞歸函數再前一次調用的變量。遞歸調用從這個位置繼續執行,這次打印的數字是6。在這次調用返回之前,堆棧的內容如下:

現在我們已經展開了整個遞歸過程,並回到該函數最初的調用。這次調用打印出數字7,也就是它的value參數除10的余數。

然後,這個遞歸函數就徹底返回到其他函數調用它的地點。
如果你把打印出來的字符一個接一個排在一起,出現在打印機或屏幕上,你將看到正確的值:4267
漢諾塔問題遞歸算法分析:
一個廟裡有三個柱子,第一個有64個盤子,從上往下盤子越來越大。要求廟裡的老和尚把這64個盤子全部移動到第三個柱子上。移動的時候始終只能小盤子壓著大盤子。而且每次只能移動一個。
1、此時老和尚(後面我們叫他第一個和尚)覺得很難,所以他想:要是有一個人能把前63個盤子先移動到第二個柱子上,我再把最後一個盤子直接移 動到第三個柱子,再讓那個人把剛才的前63個盤子從第二個柱子上移動到第三個柱子上,我的任務就完成了,簡單。所以他找了比他年輕的和尚(後面我們叫他第 二個和尚),命令:
① 你丫把前63個盤子移動到第二柱子上
② 然後我自己把第64個盤子移動到第三個柱子上後
③ 你把前63個盤子移動到第三柱子上
2、第二個和尚接了任務,也覺得很難,所以他也和第一個和尚一樣想:要是有一個人能把前62個盤子先移動到第三個柱子上,我再把最後一個盤子直接移動到第 二個柱子,再讓那個人把剛才的前62個盤子從第三個柱子上移動到第三個柱子上,我的任務就完成了,簡單。所以他也找了比他年輕的和尚(後面我們叫他第三和 尚),命令:
① 你把前62個盤子移動到第三柱子上
② 然後我自己把第63個盤子移動到第二個柱子上後
③ 你把前62個盤子移動到第二柱子上
3、第三個和尚接了任務,又把移動前61個盤子的任務依葫蘆話瓢的交給了第四個和尚,等等遞推下去,直到把任務交給了第64個和尚為止(估計第64個和尚很郁悶,沒機會也命令下別人,因為到他這裡盤子已經只有一個了)。
4、到此任務下交完成,到各司其職完成的時候了。完成回推了:
第64個和尚移動第1個盤子,把它移開,然後第63個和尚移動他給自己分配的第2個盤子。
第64個和尚再把第1個盤子移動到第2個盤子上。到這裡第64個和尚的任務完成,第63個和尚完成了第62個和尚交給他的任務的第一步。
從上面可以看出,只有第64個和尚的任務完成了,第63個和尚的任務才能完成,只有第2個和尚----第64個和尚的任務完成後,第1個和尚的任務才能完成。這是一個典型的遞歸問題。 現在我們以有3個盤子來分析:
第1個和尚命令:
① 第2個和尚你先把第一柱子前2個盤子移動到第二柱子。(借助第三個柱子)
② 第1個和尚我自己把第一柱子最後的盤子移動到第三柱子。
③ 第2個和尚你把前2個盤子從第二柱子移動到第三柱子。
很顯然,第二步很容易實現(哎,人總是自私地,把簡單留給自己,困難的給別人)。
其中第一步,第2個和尚他有2個盤子,他就命令:
① 第3個和尚你把第一柱子第1個盤子移動到第三柱子。(借助第二柱子)
② 第2個和尚我自己把第一柱子第2個盤子移動到第二柱子上。
③ 第3個和尚你把第1個盤子從第三柱子移動到第二柱子。
同樣,第二步很容易實現,但第3個和尚他只需要移動1個盤子,所以他也不用在下派任務了。(注意:這就是停止遞歸的條件,也叫邊界值)
第三步可以分解為,第2個和尚還是有2個盤子,命令:
① 第3個和尚你把第二柱子上的第1個盤子移動到第一柱子。
② 第2個和尚我把第2個盤子從第二柱子移動到第三柱子。
③ 第3個和尚你把第一柱子上的盤子移動到第三柱子。
分析組合起來就是:1→3 1→2 3→2 借助第三個柱子移動到第二個柱子 |1→3 自私人留給自己的活| 2→1 2→3 1→3借助第一個柱子移動到第三個柱子|共需要七步。
如果是4個盤子,則第一個和尚的命令中第1步和第3步各有3個盤子,所以各需要7步,共14步,再加上第1個和尚的1步,所以4個盤子總共需要移動 7+1+7=15步,同樣,5個盤子需要15+1+15=31步,6個盤子需要31+1+31=64步……由此可以知道,移動n個盤子需要(2的n次 方)-1步。
從上面整體綜合分析可知把n個盤子從1座(相當第一柱子)移到3座(相當第三柱子):
(1)把1座上(n-1)個盤子借助3座移到2座。
(2)把1座上第n個盤子移動3座。
(3)把2座上(n-1)個盤子借助1座移動3座。
下面用hanoi(n,a,b,c)表示把1座n個盤子借助2座移動到3座。
很明顯: (1)步上是 hanoi(n-1,1,3,2)
(3)步上是 hanoi(n-1,2,1,3)
用C語言表示出來,就是:
#include <stdio.h>
int method(int n,char a, char b)
{
printf("number..%d..form..%c..to..%c.."n",n,a,b);
return 0;
}
int hanoi(int n,char a,char b,char c)
{
if( n==1 ) move (1,a,c);
else
{
hanoi(n-1,a,c,b);
move(n,a,c);
hanoi(n-1,b,a,c);
};
return 0;
}
int main()
{
int num;
scanf("%d",&num);
hanoi(num,'A','B','C');
return 0;
}