海明碼(Hamming Code )是一種常用數據校驗的編碼。它是在信息位為k位,增加r位冗余位(校驗碼),構成一個n=k+r位的碼字。它可以用於檢驗數據的正誤和判別錯誤位置。
【計算海明碼】
(1)校驗位的確定
最終生成的海明碼是n位,其中k位信息位+r位冗余位(校驗碼)。r位的校驗位可以表示 2r 個數,但是只有一種表示是正確的,剩余2r -1都是錯誤的,所以若有2r -1>k+r,即可判別錯誤位置。
(2)校驗位的生成
舉例說明吧:有效信息位為1101,求它的校驗位。
①. 求所需校驗位的長度、確定校驗位位置:
根據公式2r -1>k+r,其中k=4,則r=3(這裡求r的最小整數值)。即需要3位校驗位。校驗位的位置並不是直接插在信息位的後面,而是以2的冪次方嵌入到信息位中。即分別嵌入到20、21、22 位置。
②. 求校驗位:
設校驗位分別為b1,b2,b3,則插入到信息位中後,請看圖:
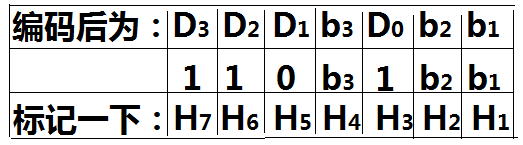
H的下標以2的冪次方形式展開:
H1:20 —— b1
H2:21 —— b2
H3:21+20 —— b1+b2
H4:22 —— b3
H5:22+20 —— b3+b1
H6:22+21 —— b3+b2
H7:22+21+20 —— b3+b2+b1
其中與 b1 有關的復合式有H3,H5,H7,與 b2 有關的有H3,H6,H7,與 b3 有關的有H5,H6,H7。將H換為對應的信息位,則:
b1 =D0 ⊕D1 ⊕D3 = 1⊕0⊕1=0
b2 =D0 ⊕D2 ⊕D3 = 1⊕1⊕1=1
b3 =D1 ⊕D2 ⊕D3 = 0⊕1⊕1=0
所以最終的海明碼為:1100110 。
【校驗數據】
待續...
本欄目