上一章我們簡單介紹了IEEE浮點標准,本次我們主要講解一下浮點運算捨入的問題,以及簡單的介紹浮點數的運算。
之前我們已經提到過,有很多小數是二進制浮點數無法准確表示的,因此就難免會遇到捨入的問題。這一點其實在我們平時的計算當中會經常出現,就比如之前我們提到過的0.3,它就是無法用浮點小數准確表示的。
為此LZ專門寫了一個小程序,使用Java語言打印出了0.3的二進制表示,是這樣的一個數字,0 01111101 00110011001100110011010。我們來簡單算一下,這個數值大約是多少。它的階碼在偏置之後的值為-2,它的尾數位在加1之後為1 + 1/8 + 1/16 + 1/128 + 1/256 = 1.19921875。後面還有有效位,不過我們只大概計算一下,就不算那麼精確了,最終算出來的值為0.2998046875。(LZ用計算器算的,0.0)
可以看出,這個值離0.3已經非常接近了,而且我們還省略了一小部分有效小數位,但是不管怎麼說,二進制無法像十進制小數一樣,准確的表示0.3這個數值。因此捨入這一部分是浮點數無法逃脫的內容。
在我們平時日常使用的十進制當中,我們一般對一個無理數或者有位數限制的有理數進行捨入時,大部分時候會采取四捨五入的方式,這算是一種比較符合我們期望的捨入方式。
不過針對浮點數來說,我們的捨入方式會更豐富一些。一共有四種方式,分別是向偶數捨入、向零捨入、向上捨入以及向下捨入。
這四種捨入方式都不難理解,其中向偶數捨入就是向最靠近的偶數捨入,比如將1.5捨入為2,將0.1捨入為0。而向零捨入則是向靠近零的值捨入,比如將1.5捨入為1,將0.1捨入為0。對於向上捨入來說,則是往大了(也就是向正無窮大)捨入的意思,比如將1.5捨入為2,將-1.5捨入為-1。而向下捨入則與向上捨入相反,是向較小的值(也就是向負無窮大)捨入的意思。
這裡需要提一下的是,除了向偶數捨入以外,其它三種方式都會有明確的邊界。這裡的含義是指這三種方式捨入後的值x'與捨入之前的值x會有一個明確的大小關系,比如對於向上捨入來說,則一定有x <= x'。對於向零捨入來說,則一定有|x| >= |x'|。
對於向偶數捨入來講,它最大的作用是在統計時使用。向偶數捨入可以讓我們在統計時,將捨入產生的誤差平均,從而盡可能的抵消。而其它三種方式在這方面都是有一定缺陷的,向上和向下捨入很明顯,會造成值的偏大或偏小。而對於向零捨入來講,如果全是正數的時候則會造成結果偏小,全是負數的時候則會造成結果偏大。
通常情況下我們采取的捨入規則是在原來的值是捨入值的中間值時,采取向偶數捨入,在二進制中,偶數我們認為是末尾為0的數。而倘若不是這種情況的話,則一般會有選擇性的使用向上和向下捨入,但總是會向最接近的值捨入。其實這正是IEEE采取的默認的捨入方式,因為這種捨入方式總是企圖向最近的值的捨入。
比如對於10.10011這個值來講,當捨入到個位數時,會采取向上捨入,因此此時的值為11。當捨入到小數點後1位時,會采取向下捨入,因此此時的值為10.1。當捨入到小數點後4位時,由於此時為10.10011捨入值的中間值,因此采用向偶數捨入,此時捨入後的值為10.1010。
之前我們講解了一堆捨入的方式,最終我們給出一個結論,就是IEEE標准默認的捨入方式,是企圖向最近的值捨入(Round to the Nearest Value)。
上面我們已經詳細的解釋了IEEE標准中默認的捨入方式(黑色加粗的那部分解釋),但是估計還是會有不少猿友比較迷糊,書中也沒有給出具體的例子,因此這裡LZ以Java語言為例,我們直接寫程序來看一下,看看Java當中的捨入方式是否是按照我們所說的進行的。
在各位看這個測試程序之前,LZ需要再給各位再解釋一下中間值的概念。中間值就是指的,比如1.1(二進制)這個數字,假設要捨入到個位,那麼它就是一個中間值,因為它處於1(二進制)和10(二進制)的中間,在這個時候將會采用向偶數捨入的方式。
下面便是LZ寫的測試程序,其中那些具體的浮點數值是使用二進制小數的算法計算出來的,各位猿友不必在意,如果你不嫌麻煩,也可以自己手算一下。我們主要看的是最終的捨入情況。
public class Main{
public static void main(String[] args){
System.out.println("捨入前: 10.10011111111111111111101");
System.out.print("捨入後:");
printFloatBinaryString(2.62499964237213134765625f);
System.out.println();
System.out.println("捨入前: 10.10011111111111111111111");
System.out.print("捨入後:");
printFloatBinaryString(2.62499988079071044921875f);
System.out.println();
System.out.println("捨入前: 10.10011111111111111111101011");
System.out.print("捨入後:");
printFloatBinaryString(2.62499968707561492919921875f);
System.out.println();
System.out.println("捨入前: 10.10011111111111111111100011");
System.out.print("捨入後:");
printFloatBinaryString(2.62499956786632537841796875f);
System.out.println();
System.out.println("捨入前: -10.10011111111111111111101");
System.out.print("捨入後:");
printFloatBinaryString(-2.62499964237213134765625f);
System.out.println();
System.out.println("捨入前: -10.10011111111111111111111");
System.out.print("捨入後:");
printFloatBinaryString(-2.62499988079071044921875f);
System.out.println();
System.out.println("捨入前: -10.10011111111111111111101011");
System.out.print("捨入後:");
printFloatBinaryString(-2.62499968707561492919921875f);
System.out.println();
System.out.println("捨入前: -10.10011111111111111111100011");
System.out.print("捨入後:");
printFloatBinaryString(-2.62499956786632537841796875f);
System.out.println();
}
public static void printFloatBinaryString(Float f){
char[] binaryChars = getBinaryChars(f);
for (int i = 0; i < binaryChars.length; i++) {
System.out.print(binaryChars[i]);
if (i == 0 || i == 8) {
System.out.print(" ");
}
}
System.out.println();
}
public static char[] getBinaryChars(Float f){
char[] result = new char[32];
char[] binaryChars = Integer.toBinaryString(Float.floatToIntBits(f)).toCharArray();
if (binaryChars.length < result.length) {
System.arraycopy(binaryChars, 0, result, result.length - binaryChars.length, binaryChars.length);
for (int i = 0; i < result.length - binaryChars.length; i++) {
result[i] = '0';
}
}else {
result = binaryChars;
}
return result;
}
}
查看本欄目
上面是測試程序,其實程序中看不出什麼,就是一堆輸出語句。如果各位猿友有興趣,也可以簡單看一下程序的實現。不過我們主要還是看結果,下面是程序結果。
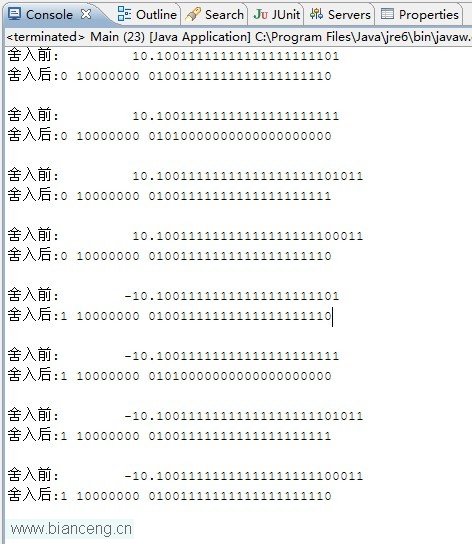
上面一共有8次捨入,前4次是正數,後4次是負數。可以看出對於正負數來講,捨入後的位表示是一樣的,只是最高位的符號位不同而已,因此這裡LZ就不再分析下面4個負數的捨入方式了,我們主要來看前4次捨入。
第1次和第2次對於末尾01和11的捨入,由於是中間值,因此全部采取的向偶數捨入的方式,保證最低位為0。第3次由於比中間值大,而數值又是正數,因此采用向上捨入的方式。第4次則比中間值小,數值也同樣是正數,因此采用向下捨入的方式。
由此可以看出,Java正是采用的我們所描述的方式進行捨入操作的,也就是總是企圖朝最近的數值捨入。相對於其它語言,由於LZ主修Java,例子篇幅也比較長,因此這裡就不寫其他語言的例子了,有興趣的猿友可以嘗試寫一下C/C++或者C#的例子來看一下,看是否是采用的同樣的捨入方式。
在IEEE標准中,制定了關於浮點數的運算規則,就是我們將把兩個浮點數運算後的精確結果的捨入值,作為我們最終的運算結果。正是因為有了這一個特殊點,就會造成浮點數當中,很多運算不滿足我們平時熟知的一些運算特性。
比如加法的結合律,也就是a + b + c = a + (b + c),這是很普通的加法運算的特性,但是浮點數是不滿這一特性的,比如說下面這一段小程序。
public static void main(String[] args){
System.out.println(1f + 10000000000f - 10000000000f);
System.out.println(1f + (10000000000f - 10000000000f));
}
這一段程序會依次輸出0.0和1.0,正是因為捨入而造成的這一誤差。在第一個輸出語句中,計算1f+10000000000f時,會將1這個有效數值捨入掉,而導致最終結果為0.0。而在第二個輸出語句中10000000000f-10000000000f將先得到結果0.0,因此最終的結果為1.0。
相應的,浮點數運算對乘法也不滿足結合律,也就是 a * b * c != a * (b * c),同時也不滿足分配律,即 a * (b + c) != a * b + a * c。
浮點數失去了很多運算方面的特性,因此也導致很多優化手段無法進行,比如我們試圖優化下面這樣一段程序。
/* 優化前 */
float x = a + b + c;
float y = b + c + d;
/* 優化後 */
float t = b + c;
float x = a + t;
float y = t + d;
對於優化前的代碼來講,進行了4次浮點運算,而優化後則是3次。然而這種優化是編譯器無法進行的,因為可能會引入誤差,比如就像前面的小例子中的結果0和1一樣。編譯器在此時一般是不敢進行優化的,試想一下,如果是銀行系統的匯款或者收款等功能,如果編譯器進行優化的話,很可能一不小心就把別人的錢給優化掉了。
文章小結
2.X系列主要講解了二進制的位表示方式、無符號以及補碼編碼以及二進制整數和浮點數的表示方式和運算。這一章是2.X的最後一章,下一章我們將進入匯編語言3.X的世界,那裡我們可以看到程序是如何使用寄存器和存儲器的、如何表示C語言中的指針、匯編語言如何實現程序的流程控制等等一系列內容。相對來講,3.X的內容會比2.X的內容有意思很多,因此希望各位猿友不要錯過。
作者:zuoxiaolong(左潇龍)
出處:博客園左潇龍的技術博客--http://www.cnblogs.com/zuoxiaolong