2.6我們進行了二進制整數運算的最後一役,本次LZ將和各位一起進入浮點數的世界,這裡沒有無符號,沒有補碼,但是有各種各樣的驚奇。倘若你真正的進入了浮點數的世界,一定會發現它原來是這麼有意思,而不是像之前一樣,覺得了解浮點數的內容沒什麼用,只要會簡單的使用就行了。當然,這其中也可能有部分猿友是覺得這部分內容太難,而對它失去了學習的興趣。
就像之前的LZ一樣,曾經對IEEE標准望而卻步,不過相信這幾章浮點數的介紹會讓你有種頓悟的感覺。倘若你有了這樣的感覺,也不要忘了“點個推薦哦。”
整數運算雖然能解決計算機當中有關信息的很大一部分儲存、運算等功能,但卻是仍然不夠的。否則假設我們要做一個超市的庫存管理系統,那麼所有商品的價格都只能是整數,這是不是讓你難以接受呢。
因此有時候我們需要更精確的數值表示,這就需要浮點數出場了。對於浮點數的表示以及運算規則,在以前是各個計算機制造商各自有一套自己的標准,這給程序的可移植性造成了很大的困擾。
有需求就有創新,最終在1985年左右,浮點數標准IEEE754就應運而生了。它就像一代秦始皇一樣,一統浮點數世界。秦始皇統一了文字、貨幣等,而IEEE754統一了浮點數的標准。
浮點數不僅僅是為了讓數值的表示更加精確,也是為了表示一些整數無法達到的數字,比如一些接近於0的數字,或者一些非常大的數值。因此浮點數對於計算機的意義,可以說是相當之大。
盡管我們本章的主要內容應該是IEEE標准,不過我們先來看看二進制是如何表示小數的,這有助於我們理解浮點數的表示。如果是一個十進制小數,相信各位都再熟悉不過了,對於12345.6789來說,它的值是由下列式子得到的。
12345.6789 = 1 * 104 + 2 * 103 + 3 * 102 + 4 * 101 + 5 * 100 + 6 * 10-1 + 7 * 10-2 + 8 * 10-3 + 9 * 10-4
這對我們來說應該是常識,那麼對於二進制小數也是類似的,考慮這樣一個小數10010.1110,它的值則可以由以下式子得到。
10010.1110 = 1 * 24 + 0 * 23 + 0 * 22 + 1 * 21 + 0 * 20 + 1 * 2-1 + 1 * 2-2 + 1 * 2-3 + 0 * 2-4 = 16 + 2 + 1/2 + 1/4 + 1/8 = 18.875
從這個角度來看,二進制小數其實與十進制小數是一樣的計算方式,只是這裡是2的整數次冪而已。
在書中給出了二進制小數的公式,對於一個形式為bm....b0.b-1....b-n的二進制小數b來說,它的值為以下計算方式。

這裡需要提醒的是,二進制小數不像整數一樣,只要位數足夠,它就可以表示所有整數。二進制小數無法精確的表示任意小數,比如最簡單的,十進制小數0.3這樣一個小數,二進制是無法精確的表示它的。
IEEE標准采用類似於科學計數法的方式表示浮點小數,即我們將每一個浮點數表示為 V = (-1)s * M * 2E 。
這其中s為符號位,為0時為正,為1時為負。M為尾數,是一個二進制小數,它的范圍是0至1-ε,或者1至2-ε(ε的值一般是2-k次方,其中設k > 0)。E為階碼,是一個二進制整數,可正可負,為了給尾數加權。
浮點格式分為兩種,一種是單精度,一種是雙精度。單雙精度分別對應於編程語言當中的float和double類型。其中float是單精度的,采用32位二進制表示,其中1位符號位,8位階碼以及23位尾數。double是雙精度的,采用64位二進制表示,其中1位符號位,11位階碼以及52位尾數。
從上面的位數上就能看出,雙精度浮點數所表示的范圍將遠遠大於單精度浮點數。針對階碼E的值,浮點數的值可以分為三種不同的情況,分別是規格化的,非規格化的以及特殊值,這三種情況就是浮點數的奧義所在了。
下面LZ首先給出一個書中對於單精度的三種情況的圖示描述,分別是1、2、3,其中3也就是特殊值又分了兩種情況3a和3b。各位猿友可以先看一下圖示的描述,接下來我們再一一具體分析。
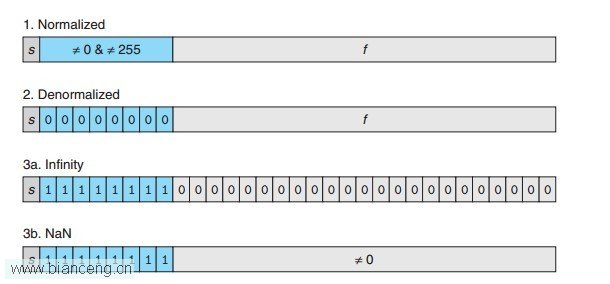
規格化的浮點數是上述的第1種情況,對於單精度來說,也就是階碼位不為0且不為255的這種情況。
在此范圍內的浮點數,階碼會被轉換成一個“偏置”後的有符號數。“偏置”的含義就是在原有的值的基礎上加上一個偏移量,對於階碼位數為k的情況來說,偏移量Bias = 2k-1-1。假設e是階碼的無符號數值,那麼真實的階碼E = e - Bias。舉個例子,假設階碼位數為8,則Bias = 127。由於8位階碼下的規格化的浮點數的階碼范圍是1至254,因此真實階碼的范圍則為-126至127。
對於尾數的解釋,則是一個小於1的小數或者0。也就是假設尾數位表示為fn-1...f0,則f的值為0.fn-1...f0。這只是尾數的值,當計算浮點數數值的時候,會在尾數值的基礎上加1,也就是真實的尾數M = 1 + f。相當於我們省掉了1位二進制,形成了浮點數表示的約定,默認尾數的值還有一個最高位的1。
非規格化的浮點數對應圖中的第2種情況,也就是階碼全為0的時候。
按照上面規格化的階碼求值方式來說,非規格化的階碼值應該固定在-Bias這個值上面。不過這裡有一個小技巧,我們設定階碼的值E = 1 - Bias。這樣做是為了能夠平滑的從非規格化的浮點數過渡到規格化的浮點數,有關這一點後面我們再詳細看。
對於尾數的解釋,非規格化的方式與規格化不同,它不會對尾數進行加1的處理,也就是說,真實的尾數M = f。這是為了能夠表示0這個數值,否則的話尾數總是大於1,那麼無論如何都將得不到0這個數值。
非規格化的浮點數除了可以表示0以外,它還有一個作用,就是可以表示接近於0的數值。另外,在浮點數當中,0的表示有兩種,一種是位表示全部為0,則為+0.0。還有一種則是符號位為1,其余全為0,此時為-0.0。
特殊值則對應圖中的3a和3b這兩種情況,也就是階碼全為1的時候。
在階碼全為1時,如果尾數位全為0,則表示無窮大。符號位為0則表示正無窮大,相反則表示負無窮大。倘若尾數位不全為0時,此時則表示NaN,表示不是一個數字。這一點在Javascript當中有一個相關的函數與這個NaN的含義有點類似,它的作用是用來判斷一個參數是否是一個數字。
下面我們來討論一下上面三種浮點數情況的取值范圍,我們假設一個浮點數有1個符號位s,k個階碼位以及n個尾數位。下面我們討論這樣一個浮點數在各個情況下的一些取值范圍。
在談論取值范圍之前,首先要說明兩點,第一點是由於特殊值的特殊性,它沒有取值范圍這一概念,因此不在我們的討論范圍之內。第二點是,由於浮點數在正負的區間內是一一對應的,因此我們將忽略符號位對取值范圍的影響,我們只討論符號位為0的情況。
對於非規格化的浮點數來說,由於階碼固定為k個0,因此真實階碼都為 E = 1 - (2k-1 - 1) = 2 - 2k-1。那麼我們可以得到下面幾個重要的取值。
1、當尾數為n個0時,此時的值為+0.0。
2、當尾數為最低位為1,其余全為0時,此時的值為最小的非0值。它此時的尾數 M = f = 2-n,因此此時的值為 2-n * 22 - 2k-1 = 2-n+2 - 2k-1。
3、當尾數為n個1時,此時的值為最大的非規格化的值。它此時的尾數 M = f = 1 - 2-n,因此此時的值為 (1 - 2-n) * 22 - 2k-1。(可能是印刷問題或是作者的筆誤,這一個值在書中寫錯了,正確的值應該是LZ給出的這個,在書中給出的這一值為 (1 - 2-n) * 2-n + 2 - 2k-1)
對於規格化的浮點數來說,同樣有三個比較重要的取值。
1、當階碼為最低位為1,其余全為0,尾數為n個0時,此時的值為最小的規格化的值。它此時的階碼恰好與非規格化的階碼相同,都為E = 2 - 2k-1。而它的尾數值則很好計算,由於尾數全部為0,則M = 1 + f = 1。因此此時的值為22 - 2k-1。
這裡需要特別提一下,對於最小的規格化的值來說,它的階碼位剛好與非規格化的值的階碼位相等,這正是因為我們將非規格化的階碼位取為1-Bias而不是-Bias的功勞。由於二者的階碼相同,而二者的尾數剛好相差2-n(2-n剛好是n位尾數時所能表示的最小精度),這正好完成了非規格化的值到規格化的值的平滑過渡。也可以看出,最小的規格化的值剛好比最大的非規格化的值大一點。
2、當階碼為最高位為0,其余全為1,尾數為n個0時,此時的值為1。因為在偏置之後,階碼E = 0 ,而尾數M = 1 + f = 1。
3、當階碼為最低位為0,其余全為1,尾數為n個1時,此時的值為最大的規格化的值。此時的階碼E = 2k-1-1,尾數M = 2 - 2-n。因此此時的值為
(2 - 2-n) * 2-1 + 2k-1,也可以化簡一下為(1 - 2-n-1) * 22k-1。
查看本欄目
書中給出了單雙精度中上述六種值的表示方式以及它們的值,我們根據上面的公式可以算出這些值,LZ這裡就不給大家一一來算了。這裡直接給出這個圖表,讓各位猿友一觀而已。(其中exp是階碼的位表示,frac是尾數的位表示)
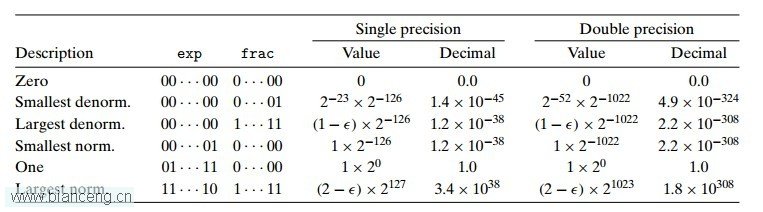
可以看出,這裡能表示的值范圍是相當大的,這對於一些需要大數值的科學研究程序或者一些應用程序來說,都是非常需要的。
這裡LZ和各位一起來看一個書中有意思的練習題,題目的原文如下。
題目:對於一種具有n位小數的浮點格式,給出不能准確描述的最小正整數的公式(因為想要准確表示它可能需要n+1位小數)。假設階碼字段長度k足夠大,可以表示的階碼范圍不會限制這個問題。
分析:首先可以排除非規格化裡的數值范圍,因為那些值全部都小於1。在考慮規格化的數值范圍裡,倘若需要n+1位小數表示,並且是最小的小數的話,則應該是由n個0和最低位的1個1組成。也就是此時的尾數M = 1 + f = 1 + 2-n-1,此時我們使用階碼抵消掉小數位,則取階碼為2n+1,因此最後的值為2n+1+1。
我們來舉個例子,考慮最簡單的,比如當n為1時,則根據上面的式子可以算出這個值為5。此時我們可以將尾數的所有值都列出來,分別為0、1/2、1、3/2。可以看出無論階碼取多少,都是不可能表示5、6、7、9等等這些數字的(任何一個大於等於5又不是2的整數次冪的值都不能表示),而像1、2、3、4這些都是可以表示的,因此最小的不能准確描述的值就是5。
本次我們主要介紹了IEEE浮點標准,本章的難度相對來說沒有上一章的難度高,因此各位猿友看起來應該不會太費力。下一章將是2.X系列的最後一章,其中主要包括浮點數的捨入以及運算部分的內容。
作者:zuoxiaolong(左潇龍)
出處:博客園左潇龍的技術博客--http://www.cnblogs.com/zuoxiaolong