程式師世界 >> 編程語言 >> 更多編程語言 >> 匯編語言 >> 計算機系統原理（九）二進制整數的加法運算和減法運算

計算機系統原理（九）二進制整數的加法運算和減法運算

編輯：匯編語言

2.3我們介紹了無符號編碼和補碼編碼，本次我們來看一下在這兩種編碼下，整數的運算是如何進行的。看後之余，別忘了“點個推薦哦。”

引言

平時的編程過程中，當進行整數運算時，經常會遇到一些奇怪的結果，比如兩個正數加出負數，兩個負數可以加出一個正數，這些都是由於數值表示的有限性導致的。下面我們來看看C語言和Java語言當中的例子。

public static void main(String[] args) {
        int a = 0x7FFFFFFF;
        int b = 0x7FFFFFFF;
        System.out.println(a);
        System.out.println(b);
        System.out.println( a + b );
    }

程序當中的a和b都是很大的正整數，結果它們相加會得到一個負數。

接下來我們再來看看C語言當中的例子，它也會具有同樣的特性。

#include <stdio.h>
    
int main(){
    int a = 0x7FFFFFFF;
    int b = 0x7FFFFFFF;
    printf("%d\n",a);
    printf("%d\n",b);
    printf("%d\n",a+b);
}

查看本欄目

無符號的非

無符號的加法會形成一個阿貝爾群，這意味著無符號加法滿足一些特性。比如可交換，可結合等等。在這個群中，單位元為0，那麼每一個群中的元素，也就是每一個無符號數u，都會擁有一個逆元u-1，滿足 u＋ u-1 = 0。這個結論的來源是，對於w位上的無符號運算來講，倘若兩個無符號數的加法運算結果為2w，也就是1後面跟w個0，此時截斷之後的結果則為0。

從以上的簡單分析，我們可以很容易的得到一個無符號數的逆元滿足以下公式（公式中的左邊就是LZ寫的u-1，由於圖中的符號在博文中不好編輯，所以LZ以u-1替代）。

補碼加法

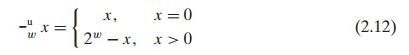
對於補碼的加法來講，我們會建立在無符號加法的基礎上來進行，這麼做的一個重要前提是，它們的位表示都是一樣的。

這裡書上寫的比較復雜，LZ這裡稍微介紹的簡單一點，其實補碼加法就是先按照無符號加法進行運算，而後在進行無符號和有符號的轉換。因此我們根據上面的結論可以得到，對於兩個補碼編碼的有符號數來說，他們進行加法運算的最終結果為，假設實際的無符號結果為sum，那麼最終的實際結果為 U2Tw(sum mod 2w)。

上面的這個結果看起來很簡單，但實際上它的運算結果還是比較復雜的，書中給出了四種情況的分析，采用數學推導和證明的方式來說明，估計對一部分數學基礎較差的猿友來講，這是一種折磨，因此LZ這裡將會省去這部分分析，如果有興趣的猿友可以私底下看一下書中的原版內容。

與無符號加法不同的是，這裡會出現三種結果，一種是正常的結果，一種是正溢出，一種是負溢出。

對於當正溢出的時候，我們的結果與無符號數類似，取模之後等價於減去2w。而當負溢出的時候，則剛好相反，取模之後的結果等價於加上2w。更直觀的，由於我們最終可表示的補碼數范圍在-2w-1（包含）到2w-1之間，所以我們總是要試圖將最終的實際結果保持在這個范圍之內。於是我們可以直觀的得到下面的結果。

補碼的非

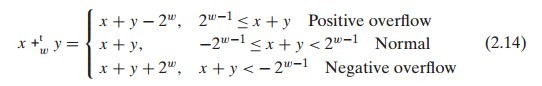
對於補碼來說，它同樣的與無符號有一樣的特性，也就是對於任意一個w位的補碼數t來說，它都有唯一的逆元t-1，使得t + t-1 = 0。

一個w位的補碼數的范圍在-2w-1（包含）到2w-1之間，直觀的可以看出，對於不等於-2w-1的補碼數x來說，它的逆元就是-x。而對於-2w-1來說，它的二進制位表示為1後面跟著w-1個0，我們需要找到一個數與其相加之後結果為0。

這種時候我們需要考慮的是，如果是-x，也就是2w-1，則它的位表示需要w+1位，是不存在的。因此我們需要考慮溢出的情況，對照上面的公式2.14，負溢出的時候需要加上2w，因此-2w-1的逆元就是-2w + 2w-1 = -2w-1，也就是它本身。

綜合上面的情況，最終我們可以得到補碼的逆元滿足以下公式（這裡與上面一樣，公式左邊是LZ所說的逆元t-1）。

二進制整數的減法

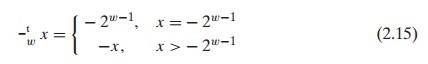
這一部分內容在書中沒有介紹，而且書中也沒有提及為什麼沒有介紹，因此LZ在這裡簡單的提上幾句。

減法運算其實是可以由加法運算替代的，我們上面已經介紹過了無符號和補碼的非，其實很多CPU是沒有減法運算器的，它們都是將減數進行逆運算以後送入加法器，然後進行加法運算，這樣得出來的結果就是減法運算最終的結果。

比如我們考慮一種簡單的情況，當w = 4時的無符號減法運算，對於 5 - 4這個減法運算來說，我們可以由 5 + 4-1（其中4-1是4的逆元的意思，不是1/4的意思）來替代這個減法運算。

為了更加直觀，LZ帶各位來算一下，首先4的逆元根據上面的公式可以得到為 4-1 = 24 - 4 = 12 。那麼我們現在需要對5和12進行加法運算，它們的位表示分別為 0101和1100，結果為10001，也就是十進制17的位表示。不過由於我們的w = 4，因此截斷之後結果為0001，也就是十進制的1。最終可以得到 5 - 4 = 1。

對於5 - 4來說，是考慮的結果為正的情況。或許有的猿友會對結果為負或者說是無符號數溢出的情況下有疑問，因此LZ這裡對這種情況也做一個簡單的介紹。我們考慮一個簡單的計算 0 - 1，我們可以得到1-1 = 24 - 1 = 15。此時對0和15進行加法運算，他們的位表示分別為0000和1111，結果為1111。

看到這裡估計有的猿友會奇怪了，這怎麼回事，0 - 1 = 15？

當然不是，這個結果其實是正確的。考慮使用補碼編碼來解析1111這個位表示，它代表的值就是-1。15是1111這個位表示在無符號編碼情況下的解析結果。

因此LZ這裡也給出一個公式，就是對於兩個整數x和y來說，x - y = x + y-1。這裡需要特別說明的是，這個公式代表的意義是位表示，而不是實際的數值。