上一章我們簡單的介紹了布爾代數以及C語言的位運算,本次我們主要來看,二進制如何表示整數,這是很重要的一章,希望各位猿友莫要錯過。
我們依然以C語言為例,C語言當中提供了多種整數類型,一共十種,位數為1、2、4、8,其中32位機器上,4位的有兩種,在64位機器上,8位的有兩種。具體的LZ這裡就不多做介紹了。以下是32位和64位系統上,這十種整數的范圍。
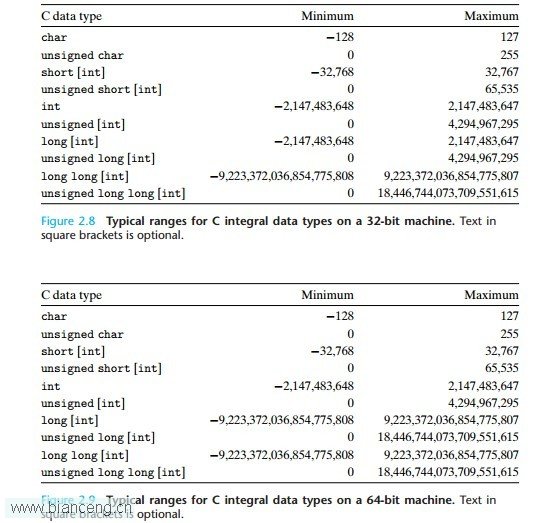
上述是C語言中各個整數類型的表示范圍,不過C語言有它的最小數值范圍,也就是說C語言要求這些數據類型至少要滿足一個標准的范圍。下圖是C語言對整數類型要求的最小表示范圍。
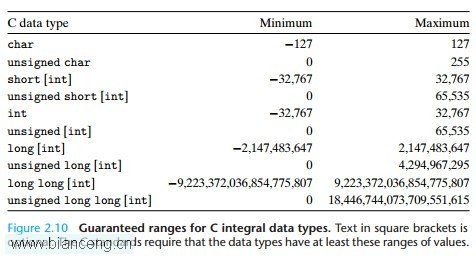
仔細看的話,可以發現,C語言只要求有符號數的范圍是對稱的,另外就是int和long類型的位數要求都比較低,分別是2位和4位。
可以看到以上的表中,每一種整數類型都可以加unsigned關鍵字,來表示一個無符號數,即沒有正負之分。在書中,給出了無符號數的定義,LZ將它簡化一下,對於一個w位的二進制來說,它的無符號表示為以下形式。

對於一個無符號編碼來說,它的最大值和最小值很好確定,對於一個w位的二進制序列來說,當所有位都為0時,則為最小值,即
UMinw = 0
而當所有位都為1時,則為最大值,根據等比數列的求和公式,即
UMaxw = 1 * (1-2w) / 1 - 2 = 2w - 1
如果把上述的定義看成是一個函數的話,那麼這個函數就是一個雙射。也就是說,對於任意整數x,當0 =< x < 2w的時候,存在唯一的二進制序列與其對應。反過來也是一樣的,對於任意一個w位的二進制序列,都存在唯一一個整數x滿足0 =< x < 2w,與這個二進制序列對應。
無符號編碼屬於相對較簡單的格式,因為它符合我們的慣性思維,上述定義其實就是對二進制轉化為十進制的公式而已,只不過在一向嚴格的數學領域來說,是要給予明確的含義的。
無符號編碼符合人的慣性思維是沒錯,但是可惜的是,它無法表示負整數。因此我們需要一種能夠表示負數的整數表示方式,這就是補碼編碼。與無符號編碼一樣,書中依然給出了補碼編碼的定義,即對於任意一個w位的二進制來說,它的補碼表示為以下形式。
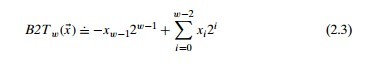
這裡最高位xw-1為符號位,當它為1時,該公式得到的值為負數,當為0時,得到的則為正數。
我們觀察這個公式,不難看出,補碼格式下,對於一個w位的二進制序列來說,當最高位為1,其余位全為0時,得到的就是補碼格式的最小值,即
TMinw = -2w-1
而當最高位為0,其余位全為1時,得到的就是補碼格式的最大值,根據等比數列的求和公式,即
TMaxw = 1 * (1 - 2w-1) / 1 - 2 = 2w-1-1
與無符號編碼一樣,如果把上述的定義看成是一個函數的話,那麼這個函數同樣是一個雙射。也就是說,對於任意整數x,當-2w-1 =< x < 2w-1的時候,存在唯一的二進制序列與其對應。反過來,對於任意一個w位的二進制序列,都存在唯一一個整數x滿足-2w-1 =< x < 2w-1,與這個二進制序列對應。
相對於無符號編碼來說,補碼編碼與我們的慣性思維有些不同,因此直觀的理解起來會有些別扭,不過作為一個程序猿,我們應該有一顆半機器的腦子,盡量去適應機器的習慣。
在C語言當中,我們經常會使用強制類型轉換,而在之前的章節中,LZ也提到過強制類型轉換。強制類型轉換不會改變二進制序列,但是會改變數據類型的大小以及解釋方式,那麼考慮相同整數類型的無符號編碼和補碼編碼,數據類型的大小是沒有任何變化的,變化的就是它們的解釋方式。比如1000這個二進制序列,如果用無符號編碼解釋的話就是表示8,而若采用補碼編碼解釋的話,則是表示-8。
考慮到上面我們已經說過,無論是無符號編碼還是補碼編碼,其映射方式都是雙射,因此它們都一定存在逆映射。如果我們定義U2Bw(x)為B2Uw(x)的逆映射,則對於任意一個整數x,如果0 =< x < 2w,經過U2Bw(x)的計算之後,將得到唯一一個二進制序列。同樣的,如果我們定義T2Bw(x)為B2Tw(x)的逆映射,則對於任意一個整數x,如果-2w-1 =< x < 2w-1,經過T2Bw(x)的計算之後,也將得到唯一一個二進制序列。
可以很明顯的看出,對於0到2w-1-1這個區間內的整數來說,兩種編碼得到的二進制序列是一樣的。為了得到其它區間裡的整數的映射關系,我們定義
T2Uw(x) = B2Uw(T2Bw(x))
這個函數代表的含義是補碼編碼轉換為無符號編碼的時候,先將補碼編碼轉換為二進制序列,再將二進制序列轉換為無符號編碼,最終也就是補碼編碼轉為無符號編碼的計算。
下面我們簡單的推算一下上面的定義,究竟是如何轉換的,也就是無符號編碼與補碼編碼的關系。我們將上面無符號編碼和補碼編碼的公式相減,
即 B2Uw(x) - B2Tw(x) = xw-12w-1 - (-xw-12w-1) = xw-12w
即 B2Uw(x) = xw-12w + B2Tw(x)
此處我們令x為T2Bw(x),則 B2Uw(T2Bw(x)) = xw-12w + B2Tw(T2Bw(x)) = xw-12w + x
即 T2Uw(x) = xw-12w + x
此時考慮xw-1的情況,當xw-1為1時,也就是補碼編碼表示負數的時候,T2Uw(x)則為2w + x 。(LZ小提示:此時x為負數,也就是說2w + x < 2w)
若xw-1為0時,則補碼編碼為正數,此時T2Uw(x) = x 。
綜上可知,有下列式子成立
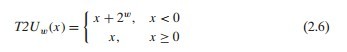
從這個式子中可以很明顯的看出,最終得到的無符號數范圍為0 =< x < 2w。
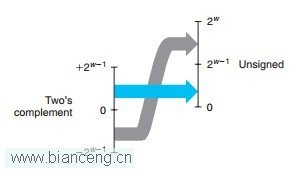
下圖為表示補碼編碼與無符號編碼的對應關系,可以看出在0至2w-1-1之間,兩者是相等的,而其余區間則不同。
查看本欄目