給定一個長度為 n 的整數列表 nums,其中 n > 1,返回輸出列表 res ,其中 res[i] 等於 nums 中除 nums[i] 之外其余各元素的乘積。
例如:
給定一個列表:[1, 2, 3, 4],返回結果:[24, 12, 8, 6]
注意:實現過程中,不允許使用 除法 ,且要求時間復雜度為O(n)
遍歷列表,對於遍歷到的當前元素,如果要計算出除其自身以外整數的乘積,我們只需要分別求出 左側所有元素的乘積 和 右側所有元素的乘積 即可。
假設給定列表為:[1, 2, 3, 4],其具體計算過程如下: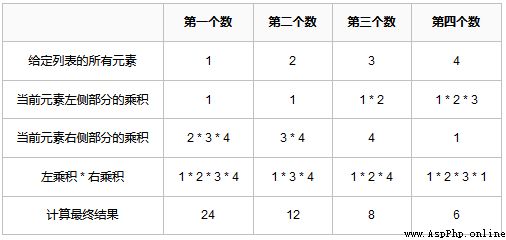
首先,正序遍歷,分別求出每個元素左側的所有元素的乘積,結果保存到 left_product_list
接著,倒序遍歷,分別求出每個元素右側的所有元素的乘積,結果保存到 right_product_list
最後,對每個遍歷到的元素,最終乘積結果 = 左乘積 * 右乘積,把結果保存到一個列表,最終返回即可
def productExceptSelf(nums):
res = []
left_product_list, right_product_list = [1], [1]
left_product, right_product = 1, 1
for i in range(1, len(nums)): # 從第一個元素開始,計算每個元素左側的所有元素的乘積
left_product *= nums[i - 1]
left_product_list.append(left_product)
for i in range(len(nums) - 2, -1, -1): # 從倒數第二個元素開始,計算每個元素右側的所有元素的乘積
right_product *= nums[i + 1]
right_product_list.append(right_product)
for i in range(len(nums)): # 注意 left_product_list 是正序計算,right_product_list 是倒序計算
left, right = left_product_list[i], right_product_list[len(nums) - 1 - i]
res.append(left * right)
return res
上面的實現方式中,我們專門定義了兩個列表:left_product_list、right_product_list,分別記錄左側元素乘積、右側元素乘積,這裡的空間復雜度是 O(n),如果我們不考慮返回列表空間的話,那麼其實可以針對上方代碼進行優化,讓其空間復雜度降到 常數級別 O(1):
def productExceptSelf(nums):
res = [1] * len(nums)
left_product, right_product = 1, 1
for i in range(1, len(nums)): # 從第一個元素開始,計算每個元素左側的所有元素的乘積
left_product *= nums[i - 1]
res[i] *= left_product
for i in range(len(nums) - 2, -1, -1): # 從倒數第二個元素開始,計算每個元素右側的所有元素的乘積
right_product *= nums[i + 1]
res[i] *= right_product
return res
上面的實現方式中,我們不再專門使用額外的列表來保存左右側元素乘積,而是將最終返回列表設置為一個固定長度的列表,接著直接修改列表中的元素值,如此一來,如果不考慮返回列表空間的前提下,其空間復雜度就降到 O(1)。
從上面的代碼中,可以發現我們對列表進行了2次遍歷,第一次正序遍歷是為了計算左乘積,第二次倒序遍歷是為了計算右乘積,在這裡其實我們也可以繼續優化,僅通過一次遍歷來完成,最終優化後代碼如下:
''' 學習中遇到問題沒人解答?小編創建了一個Python學習交流群:711312441 尋找有志同道合的小伙伴,互幫互助,群裡還有不錯的視頻學習教程和PDF電子書! '''
def productExceptSelf(nums):
""" 針對 [1, 2, 3, 4] ,遍歷過程中,每個元素的左右累積均相乘 i=0, res[0]乘左累積,res[3]乘右累積; i=1, res[1]乘左累積,res[2]乘右累積; i=2, res[2]乘左累積,res[1]乘右累積; i=3, res[3]乘左累積,res[0]乘右累積 """
res = [1] * len(nums)
left_product, right_product = 1, 1
for i in range(len(nums)):
res[i] *= left_product
left_product *= nums[i] # 下標 i 位置元素的左側所有元素的累積
res[len(nums) - 1 - i] *= right_product
right_product *= nums[len(nums) - 1 - i] # 下標 len - 1 - i 位置元素的右側所有元素的累積
return res