目錄

• 一、 機器學習概述
• • 1.1 人工智能概述
  • • 1.1.1介紹
    • 1.1.2 機器學習、深度學習能做些什麼
    • 1.1.3 人工智能階段課程安排
  • 1.2 什麼是機器學習
  • • 1.2.3 數據集構成
  • 1.3 機器學習算法分類
  • • 1.3.1 分類
    • 1.3.2 小練習
    • 1.3.3 機器學習算法分類
  • 1.4 機器學習開發流程
  • 1.5 學習框架和資料介紹
  • • 1.5.1 機器學習庫和框架
    • 1.5.2 書籍資料
• 二、特征工程
• • 2.1 數據集
  • • 2.1.1 可用數據集（針對本次三天學習而言）
    • 2.1.2 sklearn數據集
    • 2.1.3 數據集的劃分
  • 2.2 特征工程介紹
  • • 2.2.1 為什麼需要特征工程(Feature Engineering)
    • 2.2.2 什麼是特征工程
    • 2.2.3 特征工程的位置與數據處理的比較
  • 2.3 特征提取
  • • 2.3.1 特征提取
    • 2.3.2 字典特征提取
    • 2.3.3 上述總結
    • 2.3.3文本特征提取
    • 2.3.5 總結
  • 2.4 特征預處理
  • • 2.4.1 什麼是特征預處理
    • 2.4.2 歸一化
    • 2.4.3 標准化
  • 2.5 特征降維
  • • 2.5.1 降維 - 降低維度
    • 2.5.2 降維的兩種方式
    • 2.5.3 特征選擇
    • 2.5.4 低方差特征過濾
  • 2.6 主成分分析
  • • 2.6.1 什麼是主成分分析(PCA)
    • 2.6.2 案例：探究用戶對物品類別的喜好細分
• 三、分類算法
• • 3.1 sklearn轉換器和估計器
  • • 3.1.1 轉換器 - 特征工程的父類
    • 3.1.2 估計器(sklearn機器學習算法的實現)
  • 3.2 K-近鄰算法（KNN）
  • • 3.2.1 什麼是K-近鄰算法
    • 3.2.2 k-鄰近算法API
    • 3.2.3 案例1：鸢尾花種類預測
    • 3.2.4 K-近鄰總結
  • 3.3 模型選擇與調優
  • • 3.3.1 什麼是交叉驗證(cross validation)
    • 3.3.2 超參數搜索-網格搜索(Grid Search)
    • 3.3.3 鸢尾花案例增加K值調優
    • 3.2.4 案例：預測facebook簽到位置
  • 3.4 樸素貝葉斯算法
  • • 3.4.1 什麼是樸素貝葉斯分類方法
    • 3.4.2 概率基礎
    • 3.4.3 聯合概率、條件概率與相互獨立
    • 3.4.4 貝葉斯公式
    • 3.4.6 案例：20類新聞分類
    • 3.4.7 樸素貝葉斯算法總結
  • 3.5 決策樹
  • • 3.5.1 認識決策樹
    • 3.5.2 決策樹分類原理詳解
    • 3.5.3 據冊數API
    • 3.5.4 決策樹對鸢尾花分類
    • 3.5.5 決策樹可視化
    • 3.5.6 決策樹總結
    • 3.5.7 案例：泰坦尼克號乘客生存預測
  • 3.6 集成學習方法之隨機森林
  • • 3.6.1 什麼是集成學習方法
    • 3.6.2 什麼是隨機森林
    • 3.6.3 隨機森林原理過程
    • 3.6.4 API
    • 3.6.6 總結
• 四、回歸和聚類
• • 4.1 線性回歸
  • • 4.1.1 線性回歸的原理
    • 4.1.2 什麼是線性回歸
    • 4.1.2 線性回歸的損失和優化原理（理解記憶）
    • 4.1.3 線性回歸API
    • 4.1.4 波士頓房價預測
    • 4.1.5 回歸的性能評估
    • 4.1.6 正規方程和梯度下降對比
    • 4.1.7 總結
  • 4.2 欠擬合與過擬合
  • • 4.2.1 什麼是過擬合與欠擬合
    • 4.2.2 原因及解決方法
  • 4.3 線性回歸的改進-嶺回歸
  • • 4.3.1 帶有L2正則化的線性回歸-嶺回歸
  • 4.4 分類算法-邏輯回歸與二分類
  • • 4.4.1 邏輯回歸的應用場景
    • 4.4.2 邏輯回歸的原理
    • 4.4.4 案例：癌症分類預測-良／惡性乳腺癌腫瘤預測
    • 4.4.5 分類的評估方法
  • 4.5 模型保存和加載
  • • 4.5.1 sklearn模型的保存和加載API
  • 4.6 無監督學習-K-means算法
  • • 4.6.1 什麼是無監督學習
    • 4.6.2 無監督學習包含算法
    • 4.6.3 K-means原理
    • 4.6.4 API
    • 4.6.5 案例：k-means對Instacart Market用戶聚類
    • 4.6.6 Kmeans性能評估指標
    • 4.6.7 K-means總結

一、 機器學習概述

1.1 人工智能概述

1.1.1介紹

讓機器下棋（1950年人工智能），過濾垃圾郵件（1980年機器學習），圖像識別（2010年深度學習）
達特茅斯會議-人工智能的起點
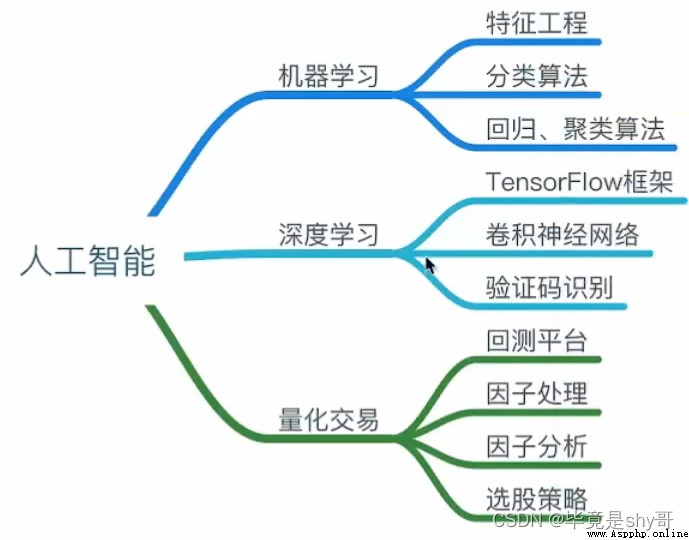
機器學習是人工智能的一個實現途徑
深度學習是機器學習的一個方法發展而來

用機器來模仿人類學習以及其他方面的智能

1.1.2 機器學習、深度學習能做些什麼

傳統預測：量化投資、廣告推薦、銷量預測
圖像識別：人臉識別、街道交通標志檢測
自然語言處理：文本分類、情感分析、自動聊天、文本檢測

1.1.3 人工智能階段課程安排

1.2 什麼是機器學習

定義：從數據中自動分析獲得模型，並利用模型對未知數據進行預測
數據、 模型、預測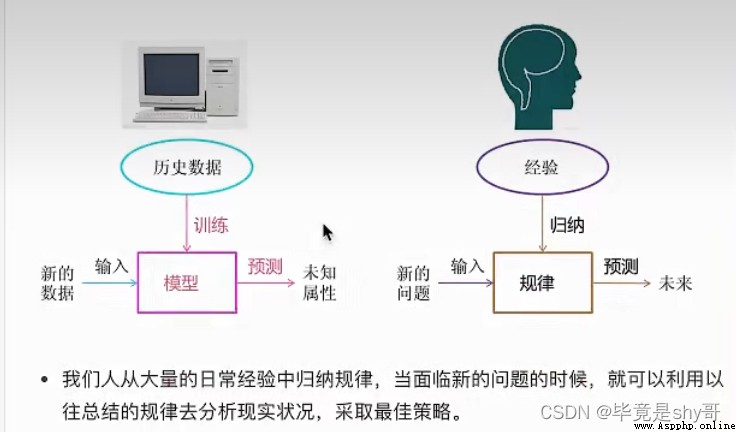

從歷史數據當中獲得規律？這些歷史數據是怎麼的格式？

1.2.3 數據集構成

結構：特征值 + 目標值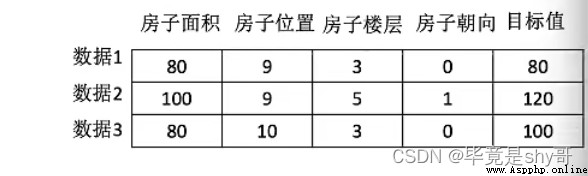

1.3 機器學習算法分類

1.3.1 分類

有目標值是監督學習

• 目標值：類別 （貓狗分類）----- 分類問題
  k-近鄰算法、貝葉斯分類、決策樹與隨機森林
• 目標值：連續型的數據 （房屋價格預測）-------回歸問題
  線性回歸、嶺回歸
• 無目標值---------- 無監督學習
  聚類 k-means

1.3.2 小練習

1、預測明天的氣溫是多少度？ 回歸
2、預測明天是陰、晴還是雨？ 分類
3、人臉年齡預測？ 回歸（多少歲）/分類（老的小的）
4、人臉識別？ 分類

1.3.3 機器學習算法分類

1.4 機器學習開發流程

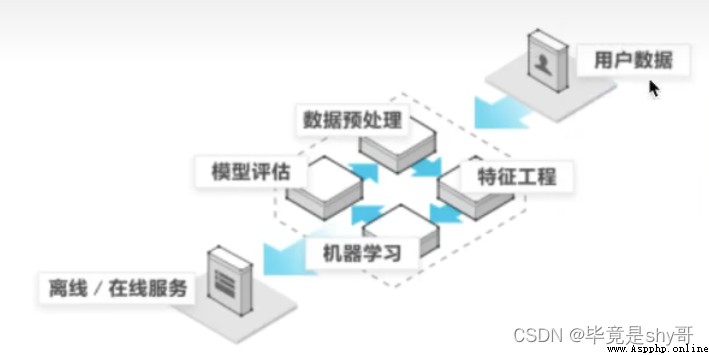
1）獲取數據
2）數據處理（缺失值什麼的）
3）特征工程（處理為能使用的數據）
4）機器學習算法訓練 - 模型
5）模型評估（模型好不好）
6）應用（不好的話返回2、3）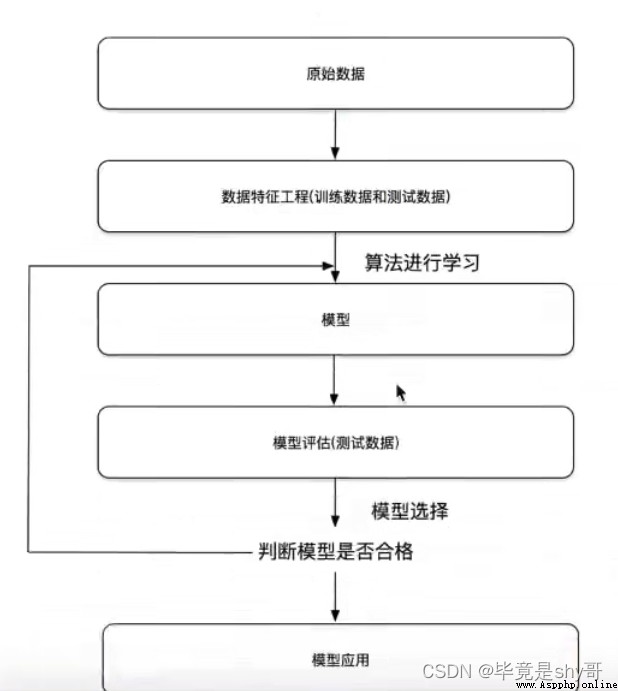

1.5 學習框架和資料介紹

1）算法是核心，數據與計算是基礎
2）找准定位

3）怎麼做？
1、入門
2、實戰類書籍
3、機器學習 -”西瓜書”- 周志華
統計學習方法 - 李航
深度學習 - “花書”
4）1.5.1 機器學習庫與框架

1.5.1 機器學習庫和框架

sklearn、tensorflow、caffe、pytorch、theano、Chainer
研究算法底層，研究框架

1.5.2 書籍資料

提升：

二、特征工程

2.1 數據集

• 分為訓練集和測試集
• 會使用sklearn的數據集

2.1.1 可用數據集（針對本次三天學習而言）

公司內部 百度
數據接口 花錢
數據集
學習階段可以用的數據集：
1）sklearn
數據量小、方便學習
2）kaggle
大數據競賽平台、80萬科學家、真實數據、數據量巨大
3）UCI
目前600多數據集、領域廣、數據量幾十萬

1. Scikit-learn工具介紹
   
2. 安裝

pip3 install Scikit-learn==0.19.1

3. Scikit-learn包含的內容
   

2.1.2 sklearn數據集

1. scikit-learn數據集API介紹
   
2. sklearn小數據集
   
3. sklearn大數據集
   
4. sklearn數據集的使用
   
5. 數據集的返回值
   datasets.base.Bunch（繼承自字典）
   dict[“key”] = values
   bunch.key = values 思考：拿到的數據是否全部都用來訓練一個模型？
   no,測試集

2.1.3 數據集的劃分

• 訓練數據：用於訓練，構建模型
• 測試數據：在模型檢驗時使用，用於評估模型是否有效
  測試集 20%~30%
  
  sklearn.model_selection.train_test_split(arrays, *options)
  訓練集特征值，測試集特征值，訓練集目標值，測試集目標值
  x_train, x_test, y_train, y_test
  

2.2 特征工程介紹

影響訓練效果的原因：算法、特征工程

2.2.1 為什麼需要特征工程(Feature Engineering)

2.2.2 什麼是特征工程

2.2.3 特征工程的位置與數據處理的比較

sklearn 特征工程
pandas 數據清洗、數據處理直接
特征抽取/特征提取（有些數據不能處理，需要轉換）
機器學習算法 - 統計方法 - 數學公式
文本類型 -》 數值
類型 -》 數值

2.3 特征提取

2.3.1 特征提取

sklearn.feature_extraction

2.3.2 字典特征提取

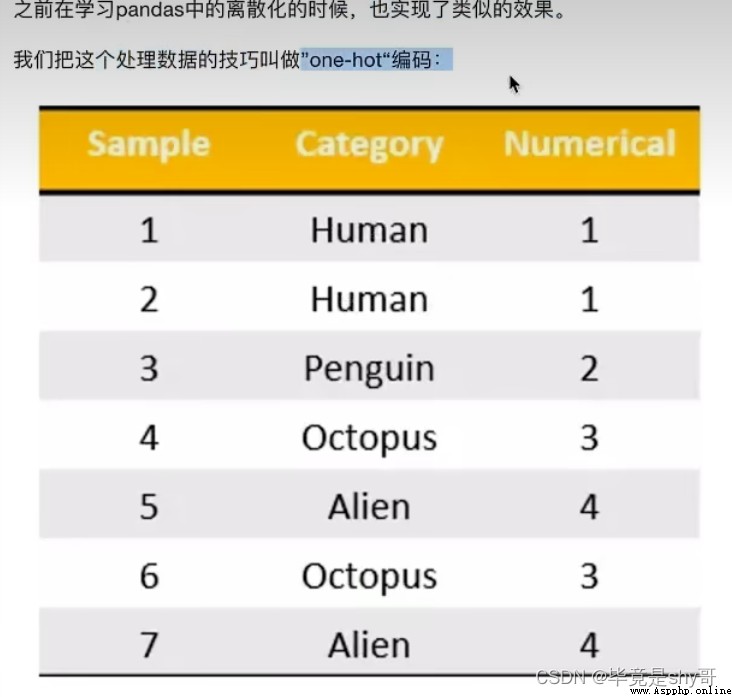
類別 -> one-hot編碼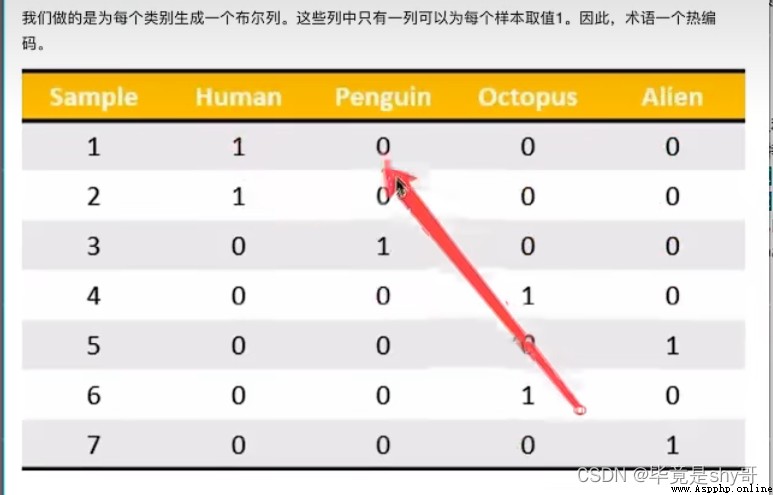

sklearn.feature_extraction.DictVectorizer(sparse=True,…)
vector 數學：向量 物理：矢量
矩陣 matrix 二維數組
向量 vector 一維數組
父類：轉換器類
返回sparse矩陣
sparse稀疏
將非零值 按位置表示出來
節省內存 - 提高加載效率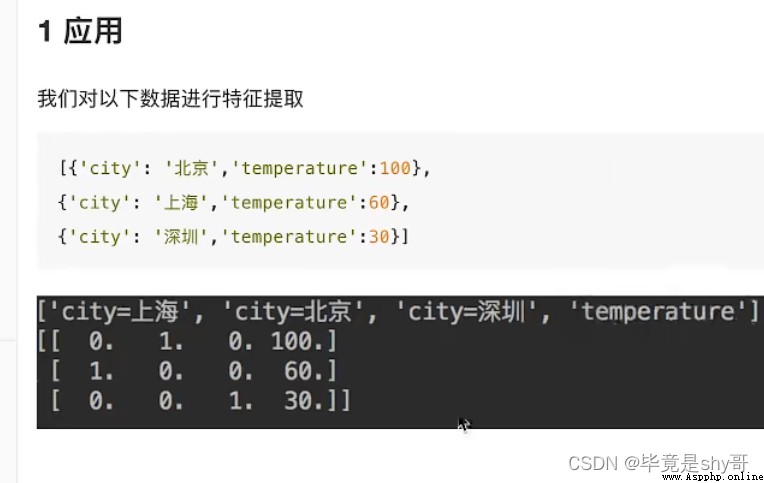

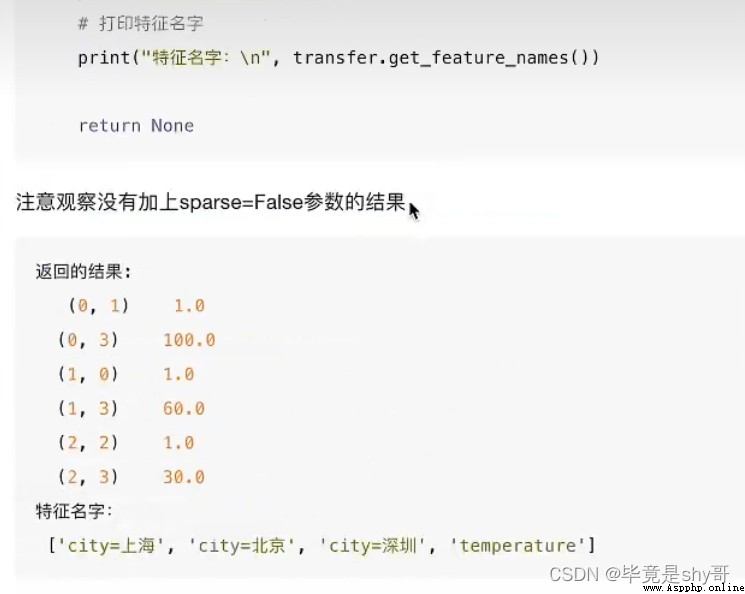
轉化為：

2.3.3 上述總結

對於特征當中存在類別信息的我們都會做one-hot編碼處理

應用場景：
1）pclass, sex 數據集當中類別特征比較多
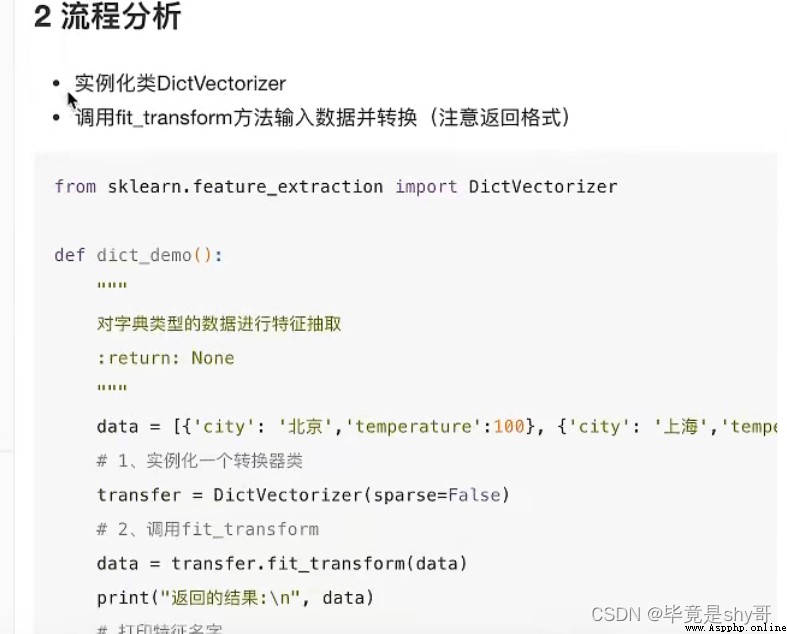
1、將數據集的特征-》字典類型
2、DictVectorizer轉換
2）本身拿到的數據就是字典類型

2.3.3文本特征提取

作用：對文本數據進行特征值化
單詞 作為 特征
句子、短語、單詞、字母
特征：特征詞

• 方法1：CountVectorizer
  統計每個樣本特征詞出現的個數
  stop_words停用的
  停用詞表

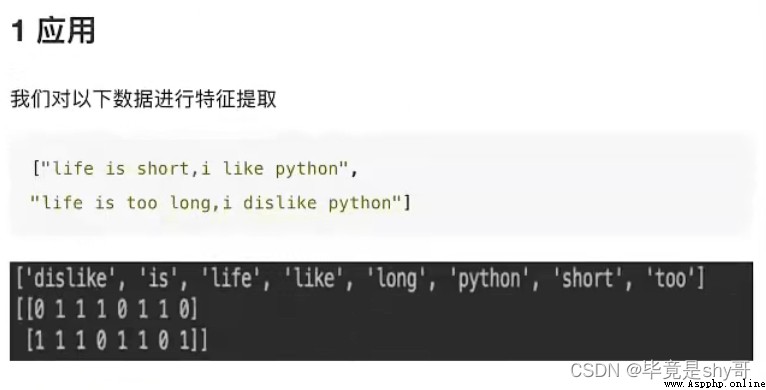
關鍵詞：在某一個類別的文章中，出現的次數很多，但是在其他類別的文章當中出現很少

• 方法2：TfidfVectorizer
  
  

TF-IDF - 重要程度
兩個詞 “經濟”，“非常”
1000篇文章-語料庫
100篇文章 - “非常”
10篇文章 - “經濟”
兩篇文章
文章A(100詞) : 10次“經濟” TF-IDF:0.2
tf:10/100 = 0.1
idf:lg 1000/10 = 2
文章B(100詞) : 10次“非常” TF-IDF:0.1
tf:10/100 = 0.1
idf: log 10 1000/100 = 1

TF - 詞頻（term frequency，tf)
IDF - 逆向文檔頻率

2.3.5 總結

對字典的類別轉換為onehot編碼
對文本：1. 統計特征值出現的個數 2. 計算詞的重要性程度

2.4 特征預處理

2.4.1 什麼是特征預處理

為什麼我們要進行歸一化/標准化？
無量綱化

2.4.2 歸一化

異常值：最大值、最小值

2.4.3 標准化

(x - mean) / std
均值變化不會太大
標准差：集中程度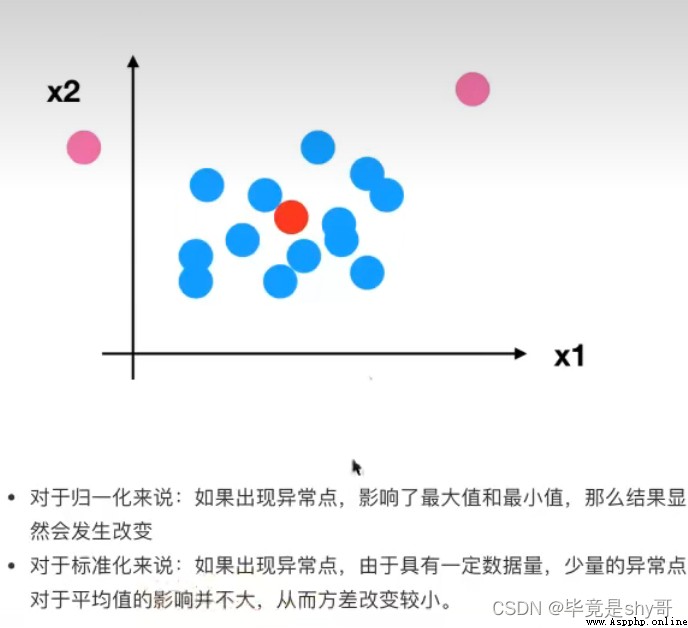

應用場景：
在已有樣本足夠多的情況下比較穩定，適合現代嘈雜大數據場景。

2.5 特征降維

2.5.1 降維 - 降低維度

ndarray
維數：嵌套的層數
0維 標量
1維 向量
2維 矩陣
3維
n維
二維數組
此處的降維：降低特征的個數（列數）
效果：
特征與特征之間不相關

2.5.2 降維的兩種方式

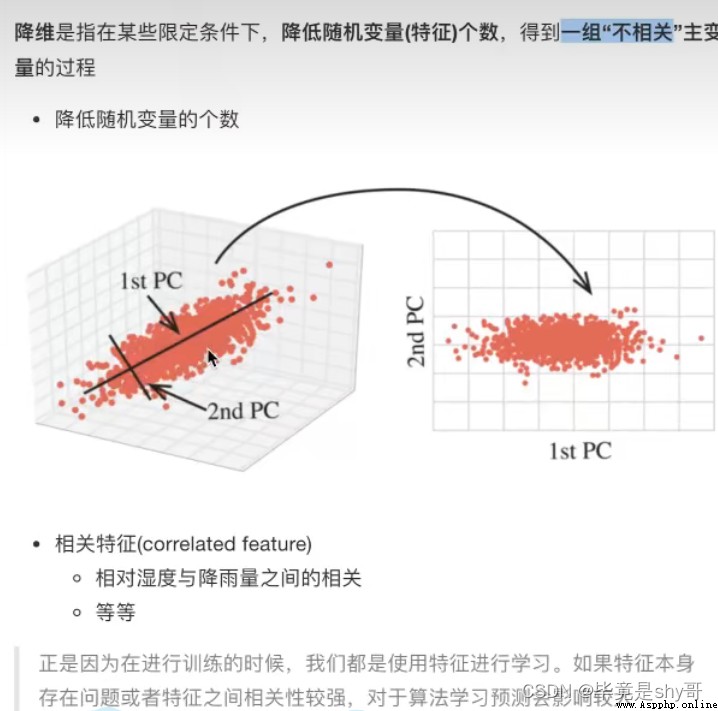
• 特征選擇
• 主成分分析（理解為一種特征提取的方式）

2.5.3 特征選擇

特征選擇

• Filter過濾式
  方差選擇法：低方差特征過濾
  相關系數 - 特征與特征之間的相關程度
  取值范圍：–1≤ r ≤+1
  皮爾遜相關系數
  0.9942
  特征與特征之間相關性很高：
  1）選取其中一個
  2）加權求和
  3）主成分分析
• Embeded嵌入式
  決策樹 第二天
  正則化 第三天
  深度學習 第五天

2.5.4 低方差特征過濾

2.6 主成分分析

2.6.1 什麼是主成分分析(PCA)

sklearn.decomposition.PCA(n_components=None)
n_components
小數 表示保留百分之多少的信息
整數 減少到多少特征

2.6.2 案例：探究用戶對物品類別的喜好細分

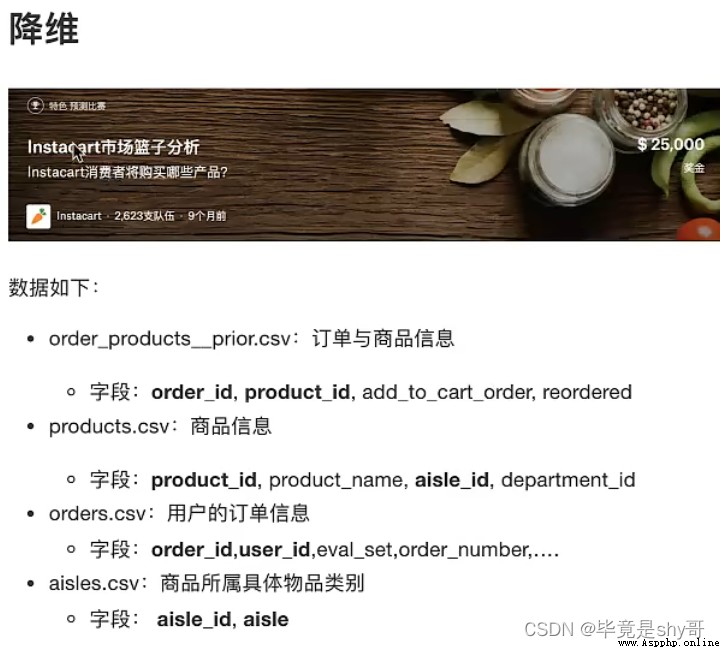
用戶 物品類別
user_id aisle
1）需要將user_id和aisle放在同一個表中 - 合並
2）找到user_id和aisle - 交叉表和透視表
3）特征冗余過多 -> PCA降維

三、分類算法

目標值：類別

1、sklearn轉換器和預估器
2、KNN算法
3、模型選擇與調優
4、樸素貝葉斯算法
5、決策樹
6、隨機森林

3.1 sklearn轉換器和估計器

轉換器
估計器(estimator)

3.1.1 轉換器 - 特征工程的父類

1 實例化 (實例化的是一個轉換器類(Transformer))
2 調用fit_transform(對於文檔建立分類詞頻矩陣，不能同時調用)
標准化：
(x - mean) / std
fit_transform()
fit() 計算 每一列的平均值、標准差
transform() (x - mean) / std進行最終的轉換

3.1.2 估計器(sklearn機器學習算法的實現)

估計器工作流程：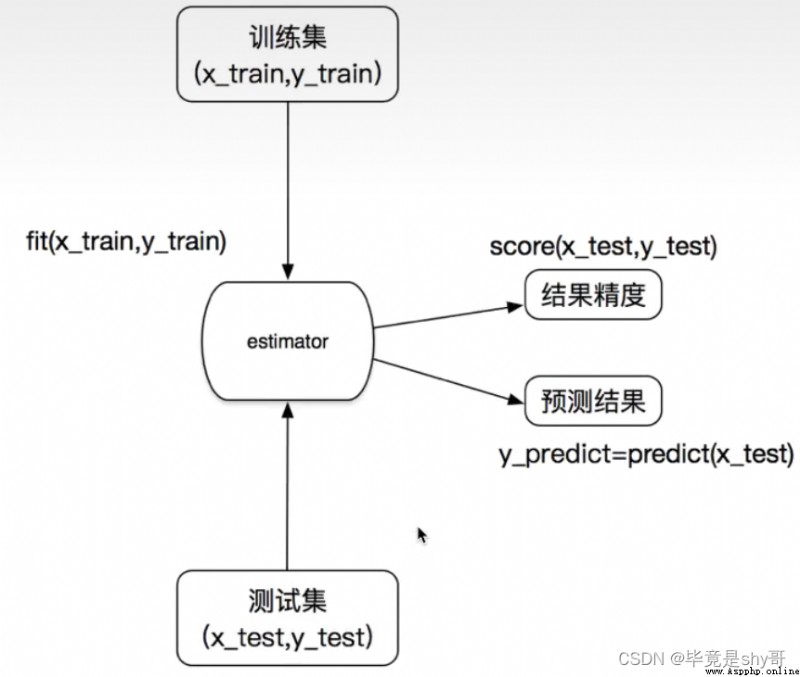
估計器(estimator)
1 實例化一個estimator
2 estimator.fit(x_train, y_train) 計算 —— 調用完畢，模型生成
3 模型評估：
1）直接比對真實值和預測值
y_predict = estimator.predict(x_test)
y_test == y_predict
2）計算准確率
accuracy = estimator.score(x_test, y_test)

3.2 K-近鄰算法（KNN）

3.2.1 什麼是K-近鄰算法

KNN核心思想：
你的“鄰居”來推斷出你的類別

1. K-近鄰算法(KNN)原理
   
   k = 1
   容易受到異常點的影響
   如何確定誰是鄰居？
   計算距離：
   距離公式
   歐氏距離
   曼哈頓距離 絕對值距離
   明可夫斯基距離
2. 電影類型分析
   k = 1 愛情片
   k = 2 愛情片
   ……
   k = 6 無法確定
   k = 7 動作片

如果取的最近的電影數量不一樣？會是什麼結果？
k 值取得過小，容易受到異常點的影響
k 值取得過大，樣本不均衡的影響
結合前面的約會對象數據，分析K-近鄰算法需要做什麼樣的處理
無量綱化的處理
標准化

3.2.2 k-鄰近算法API

sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,algorithm=‘auto’)
n_neighbors：k值

3.2.3 案例1：鸢尾花種類預測

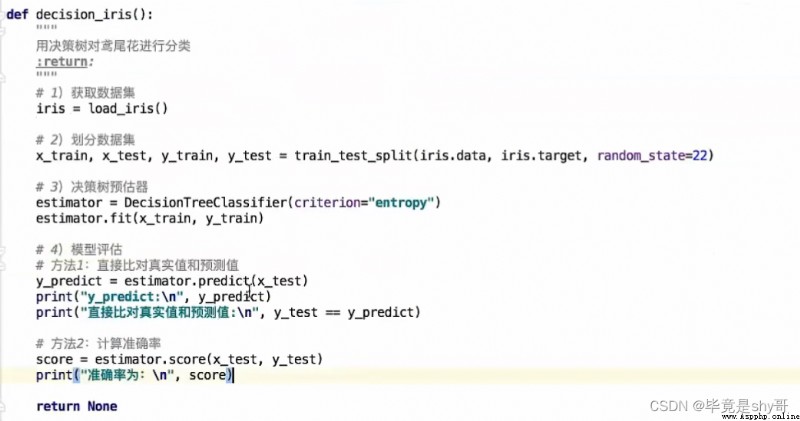
1）獲取數據
2）數據集劃分
3）特征工程
標准化
4）KNN預估器流程
5）模型評估

3.2.4 K-近鄰總結

優點：簡單，易於理解，易於實現，無需訓練
缺點：
1）必須指定K值，K值選擇不當則分類精度不能保證
2）懶惰算法，對測試樣本分類時的計算量大，內存開銷大
使用場景：小數據場景，幾千～幾萬樣本，具體場景具體業務去測試

3.3 模型選擇與調優

3.3.1 什麼是交叉驗證(cross validation)

3.3.2 超參數搜索-網格搜索(Grid Search)

k的取值
[1, 3, 5, 7, 9, 11]
暴力破解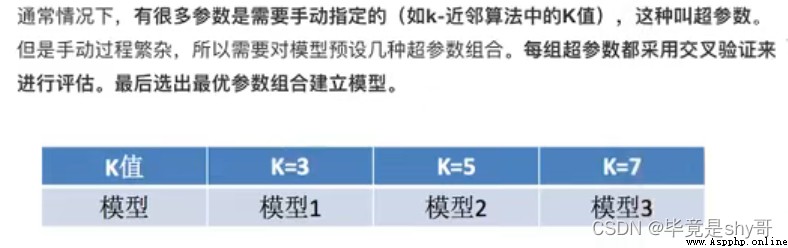

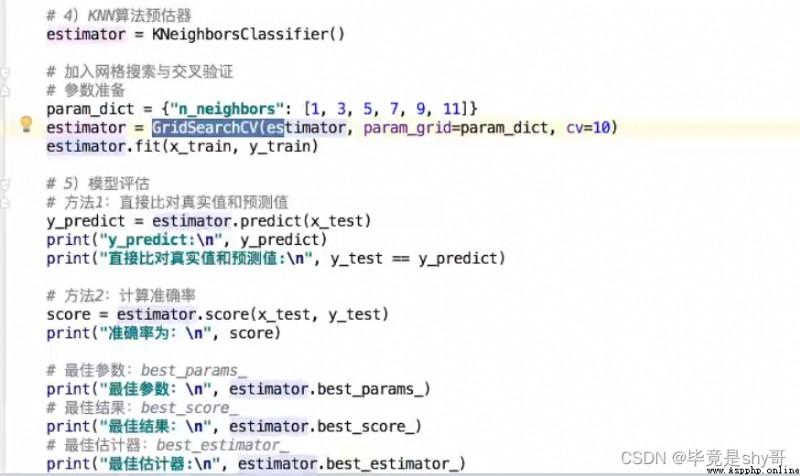
3.3.3 鸢尾花案例增加K值調優

3.2.4 案例：預測facebook簽到位置

流程分析：
1）獲取數據
2）數據處理
目的：
特征值 x
目標值 y
a.縮小數據范圍
2 < x < 2.5
1.0 < y < 1.5
b.time -> 年月日時分秒
c.過濾簽到次數少的地點
數據集劃分
3）特征工程：標准化
4）KNN算法預估流程
5）模型選擇與調優
6）模型評估

3.4 樸素貝葉斯算法

3.4.1 什麼是樸素貝葉斯分類方法

分完之後出現概率值

3.4.2 概率基礎

1 概率(Probability)定義

3.4.3 聯合概率、條件概率與相互獨立

• 聯合概率：包含多個條件，且所有條件同時成立的概率
  P(程序員, 勻稱) P(程序員, 超重|喜歡)
  P(A, B)
• 條件概率：就是事件A在另外一個事件B已經發生條件下的發生概率
  P(程序員|喜歡) P(程序員, 超重|喜歡)
  P(A|B)
• 相互獨立:
  P(A, B) = P(A)P(B) <=> 事件A與事件B相互獨立

3.4.4 貝葉斯公式

樸素？
假設：特征與特征之間是相互獨立

樸素貝葉斯算法：
樸素 + 貝葉斯
應用場景：
文本分類

單詞作為特征

拉普拉斯平滑系數

3.4.6 案例：20類新聞分類

1）獲取數據
2）劃分數據集
3）特征工程
文本特征抽取
4）樸素貝葉斯預估器流程
5）模型評估

3.4.7 樸素貝葉斯算法總結

3.5 決策樹

3.5.1 認識決策樹

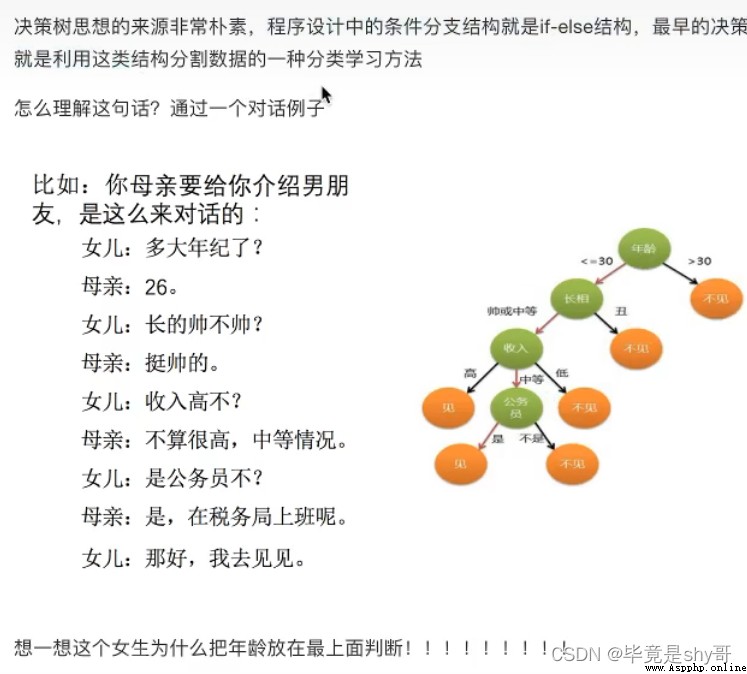
如何高效的進行決策？
特征的先後順序

3.5.2 決策樹分類原理詳解

已知 四個特征值 預測 是否貸款給某個人
先看房子，再工作 -> 是否貸款 只看了兩個特征
年齡，信貸情況，工作 看了三個特征

3.5.3 據冊數API

信息論基礎
1）信息
香農：消除隨機不定性的東西
小明 年齡 “我今年18歲” - 信息
小華 ”小明明年19歲” - 不是信息
2）信息的衡量 - 信息量 - 信息熵
bit
g(D,A) = H(D) - 條件熵H(D|A)
4 決策樹的劃分依據之一------信息增益
沒有免費的午餐

3.5.4 決策樹對鸢尾花分類

3.5.5 決策樹可視化

3.5.6 決策樹總結

優點：
可視化 - 可解釋能力強
缺點：
容易產生過擬合

3.5.7 案例：泰坦尼克號乘客生存預測

流程分析：
特征值 目標值
1）獲取數據
2）數據處理
缺失值處理
特征值 -> 字典類型
3）准備好特征值 目標值
4）劃分數據集
5）特征工程：字典特征抽取
6）決策樹預估器流程
7）模型評估

3.6 集成學習方法之隨機森林

3.6.1 什麼是集成學習方法

3.6.2 什麼是隨機森林

隨機
森林：包含多個決策樹的分類器

3.6.3 隨機森林原理過程

訓練集：
N個樣本
特征值 目標值
M個特征
隨機
兩個隨機

• 訓練集隨機 - N個樣本中隨機有放回的抽樣N個
  bootstrap 隨機有放回抽樣
  [1, 2, 3, 4, 5]
  新的樹的訓練集
  [2, 2, 3, 1, 5]
• 特征隨機 - 從M個特征中隨機抽取m個特征
  M >> m
  降維
  

3.6.4 API

3.6.6 總結

能夠有效地運行在大數據集上，
處理具有高維特征的輸入樣本，而且不需要降維

四、回歸和聚類

線性回歸
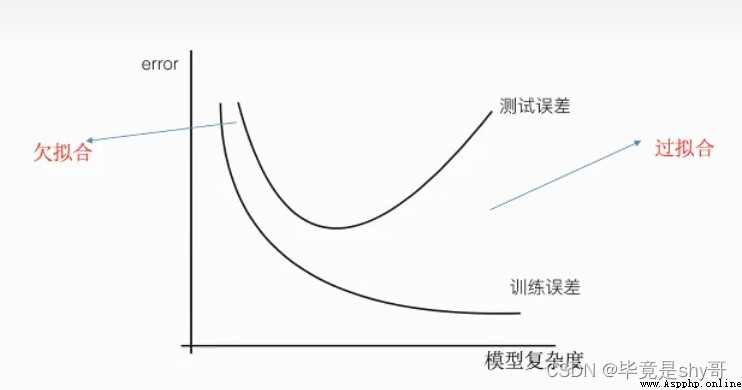
欠擬合與過擬合
嶺回歸

分類算法：邏輯回歸

模型保存與加載

無監督學習 K-means算法

4.1 線性回歸

回歸問題：
目標值 - 連續型的數據

4.1.1 線性回歸的原理

4.1.2 什麼是線性回歸

函數關系 ：特征值和目標值
線型模型
線性關系
y = w1x1 + w2x2 + w3x3 + …… + wnxn + b
= wTx + b
數據挖掘基礎
y = kx + b
y=w1x1+w2x2+b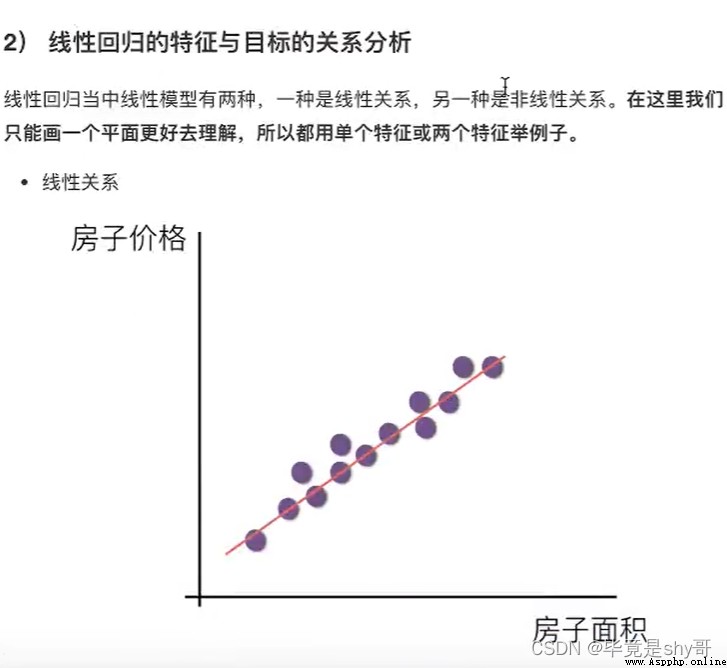

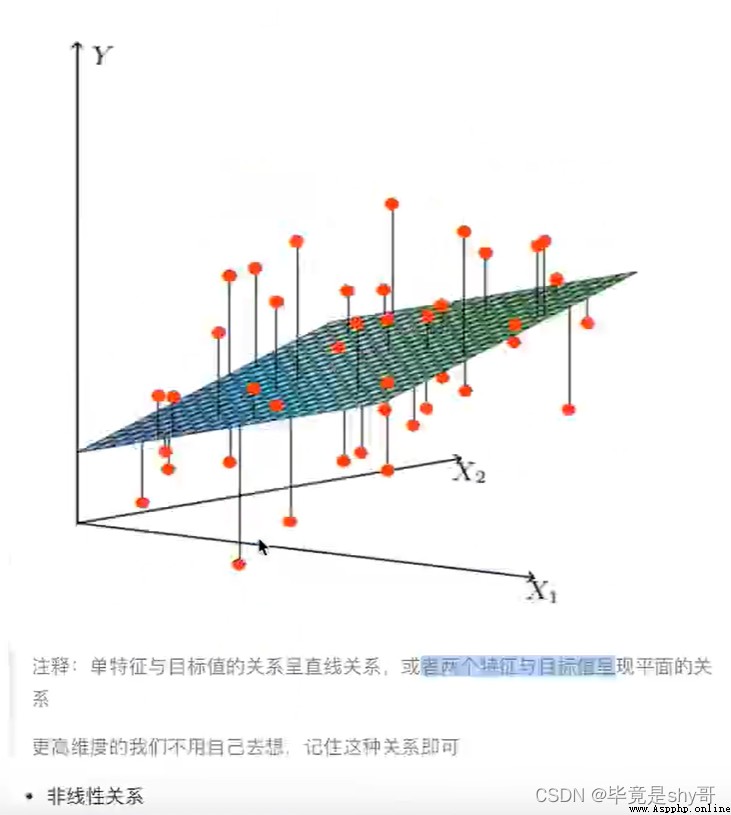
廣義線性模型
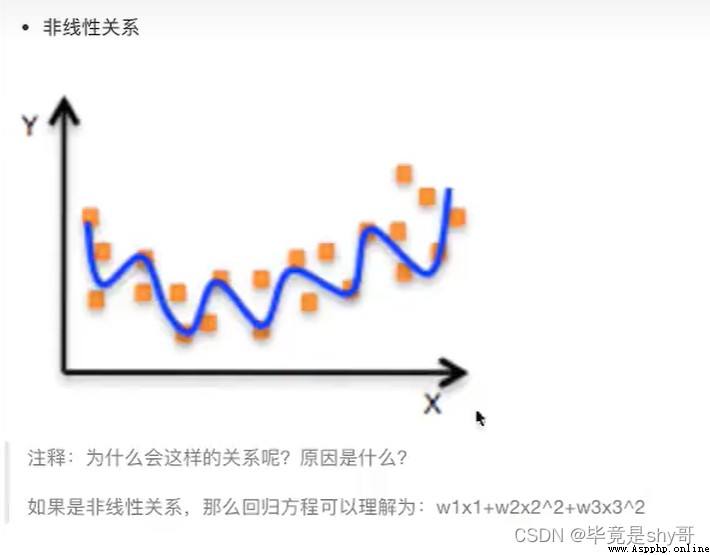
也有非線性關系
線性模型
自變量一次(線性關系)
y = w1x1 + w2x2 + w3x3 + …… + wnxn + b
參數一次
y = w1x1 + w2x1^2 + w3x1^3 + w4x2^3 + …… + b（w1,w2,w3是一次的）
線性關系&線性模型
線性關系一定是線性模型
線性模型不一定是線性關系

4.1.2 線性回歸的損失和優化原理（理解記憶）

目標：求模型參數
模型參數能夠使得預測准確
真實關系：真實房子價格 = 0.02×中心區域的距離 + 0.04×城市一氧化氮濃度 + (-0.12×自住房平均房價) + 0.254×城鎮犯罪率
隨意假定：預測房子價格 = 0.25×中心區域的距離 + 0.14×城市一氧化氮濃度 + 0.42×自住房平均房價 + 0.34×城鎮犯罪率
損失函數/cost/成本函數/目標函數：

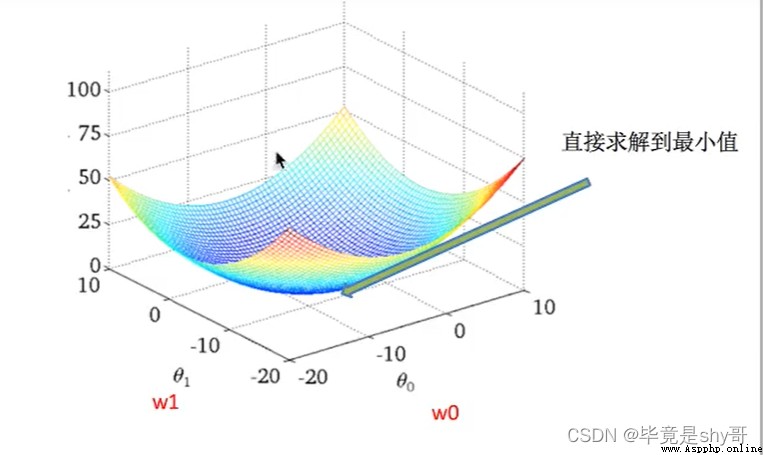
• 正規方程
  天才 - 直接求解W

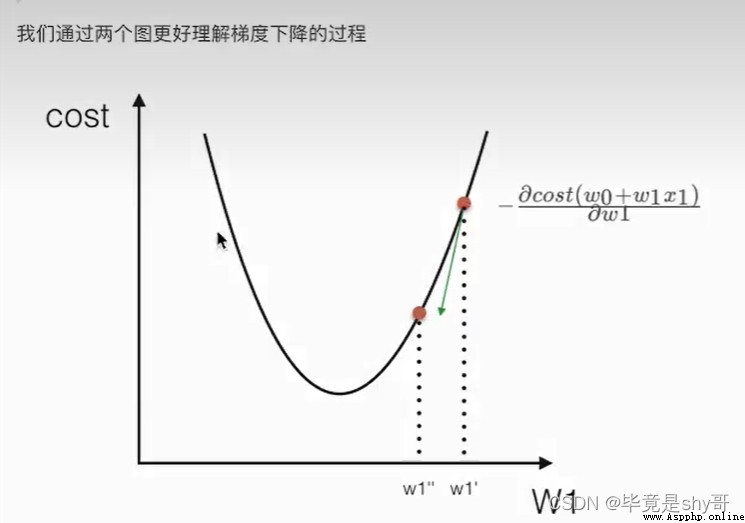
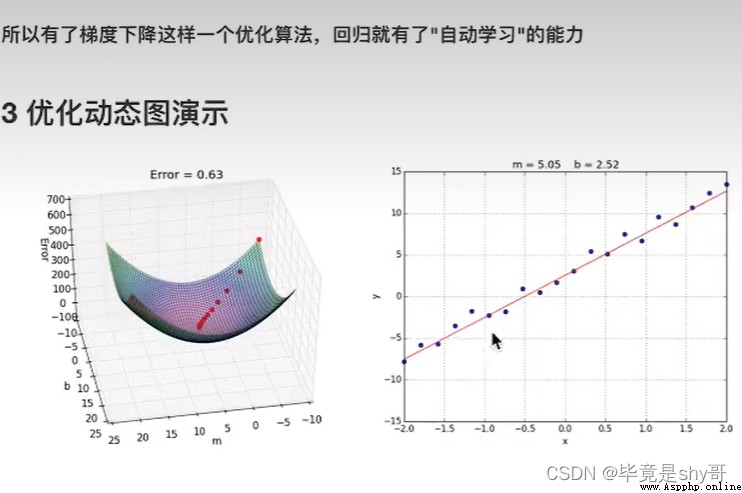
• 梯度下降

勤奮努力的普通人
試錯、改進

4.1.3 線性回歸API

4.1.4 波士頓房價預測

流程：
1）獲取數據集
2）劃分數據集
3）特征工程：
無量綱化 - 標准化
4）預估器流程
fit() --> 模型
coef_ intercept_
5）模型評估

4.1.5 回歸的性能評估

均方誤差

4.1.6 正規方程和梯度下降對比

4.1.7 總結

4.2 欠擬合與過擬合

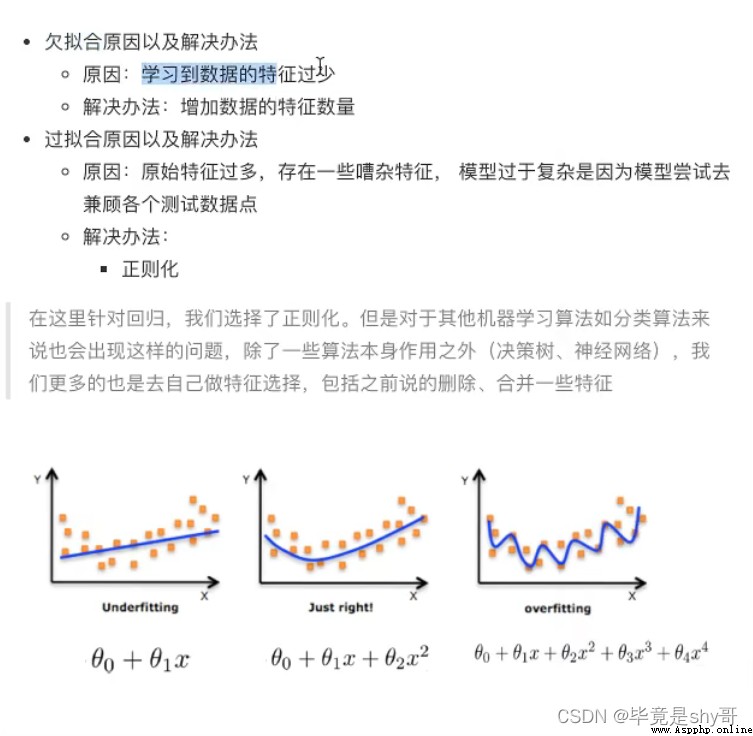
訓練集上表現得好，測試集上不好 - 過擬合

4.2.1 什麼是過擬合與欠擬合

• 欠擬合（學習的少，偷懶）

學習到數據的特征過少
解決：
增加數據的特征數量

• 過擬合（想面面俱到，想太多）
  原始特征過多，存在一些嘈雜特征， 模型過於復雜是因為模型嘗試去兼顧各個測試數據點
  解決：
  正則化
  
  
  

4.2.2 原因及解決方法

L1
損失函數 + λ懲罰項
LASSO
L2 更常用
損失函數 + λ懲罰項
Ridge - 嶺回歸

4.3 線性回歸的改進-嶺回歸

4.3.1 帶有L2正則化的線性回歸-嶺回歸

1. API
   
   

alpha 正則化力度=懲罰項系數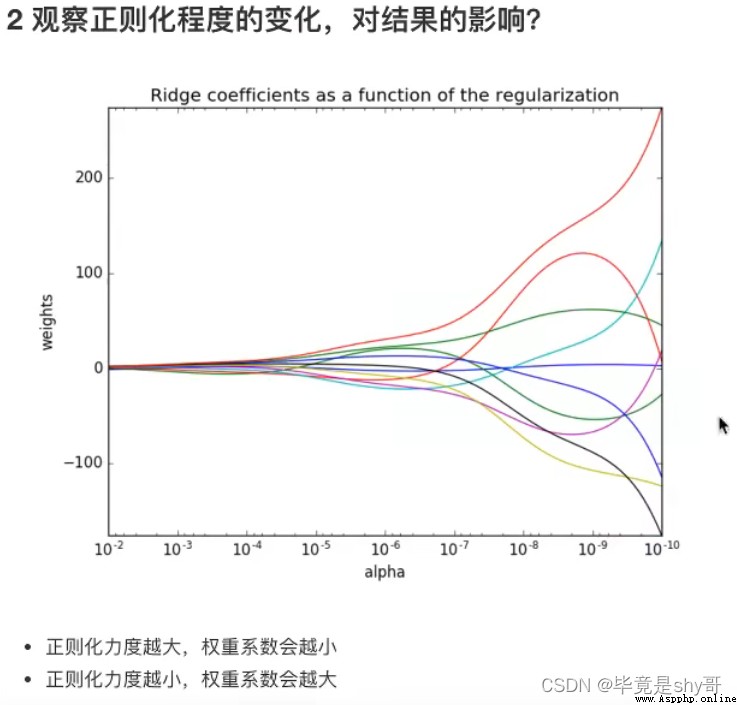

4.4 分類算法-邏輯回歸與二分類

4.4.1 邏輯回歸的應用場景

廣告點擊率 是否會被點擊
是否為垃圾郵件
是否患病
是否為金融詐騙
是否為虛假賬號
正例 / 反例

4.4.2 邏輯回歸的原理

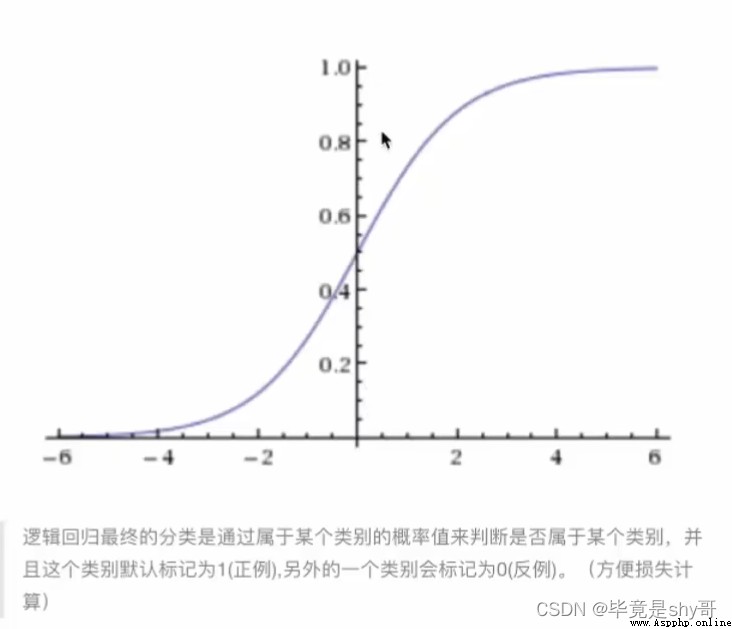
線型回歸的輸出 就是 邏輯回歸 的 輸入

• 激活函數
  sigmoid函數 [0, 1]
  1/(1 + e^(-x))
  假設函數/線性模型
  1/(1 + e^(-(w1x1 + w2x2 + w3x3 + …… + wnxn + b)))

• 損失函數
  (y_predict - y_true)平方和/總數
  邏輯回歸的真實值/預測值 是否屬於某個類別

• 對數似然損失
  log 2 x
  
  
  
  
  
  

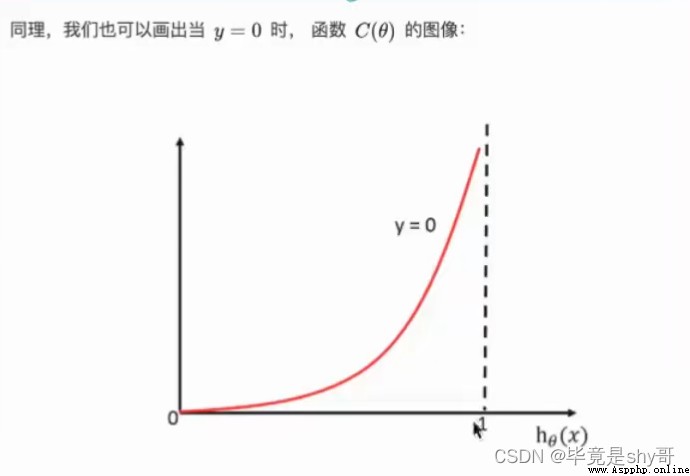
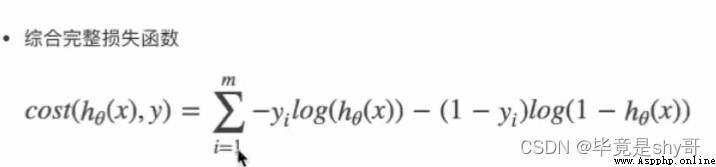
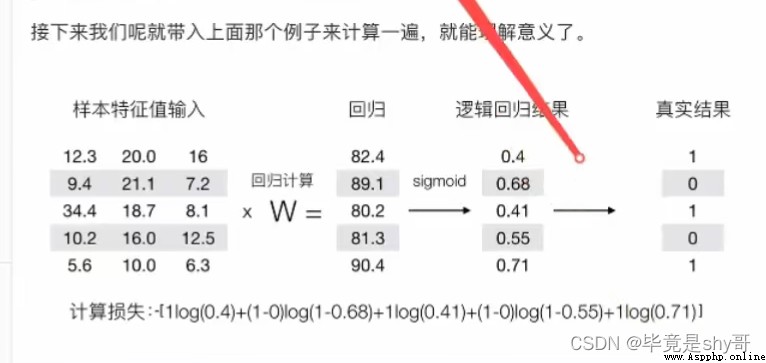
• 優化損失
  梯度下降
  

4.4.4 案例：癌症分類預測-良／惡性乳腺癌腫瘤預測

惡性 - 正例
流程分析：
1）獲取數據
讀取的時候加上names
2）數據處理
處理缺失值
3）數據集劃分
4）特征工程：
無量綱化處理-標准化
5）邏輯回歸預估器
6）模型評估
真的患癌症的，能夠被檢查出來的概率 - 召回率

4.4.5 分類的評估方法

1. 精確率與召回率
   
   
   
   

1 混淆矩陣
TP = True Possitive
FN = False Negative
2 精確率(Precision)與召回率(Recall)
精確率
召回率 查得全不全
工廠 質量檢測 次品 召回率
3 F1-score 模型的穩健型
總共有100個人，如果99個樣本癌症，1個樣本非癌症 - 樣本不均衡
不管怎樣我全都預測正例(默認癌症為正例) - 不負責任的模型
准確率：99%
召回率：99/99 = 100%
精確率：99%
F1-score: 2*99%/ 199% = 99.497%
AUC:0.5
TPR = 100%
FPR = 1 / 1 = 100%

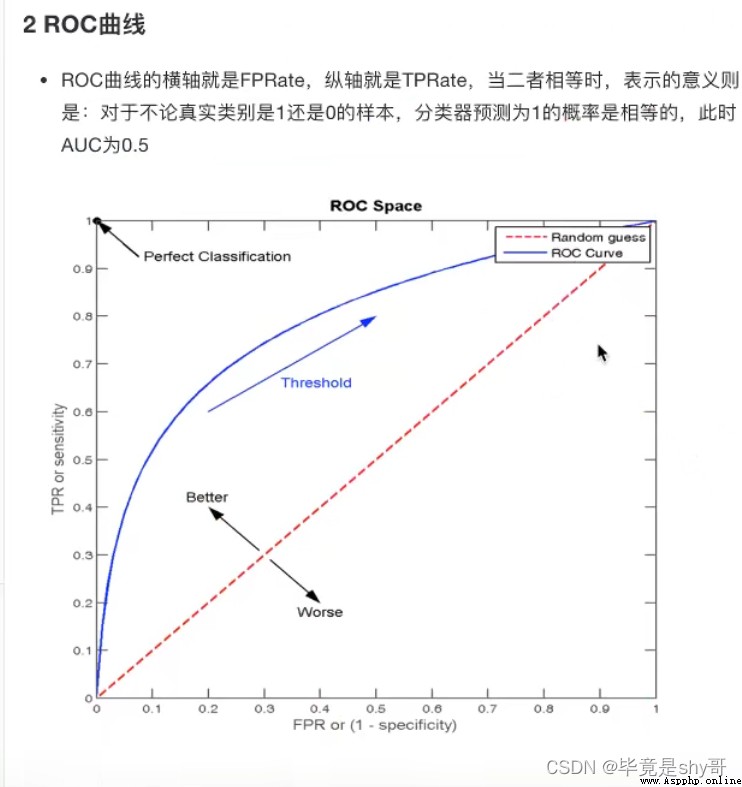
2 ROC曲線與AUC指標
1 知道TPR與FPR
TPR = TP / (TP + FN) - 召回率
所有真實類別為1的樣本中，預測類別為1的比例
FPR = FP / (FP + TN)
所有真實類別為0的樣本中，預測類別為1的比例

4.5 模型保存和加載

4.5.1 sklearn模型的保存和加載API

4.6 無監督學習-K-means算法

4.6.1 什麼是無監督學習

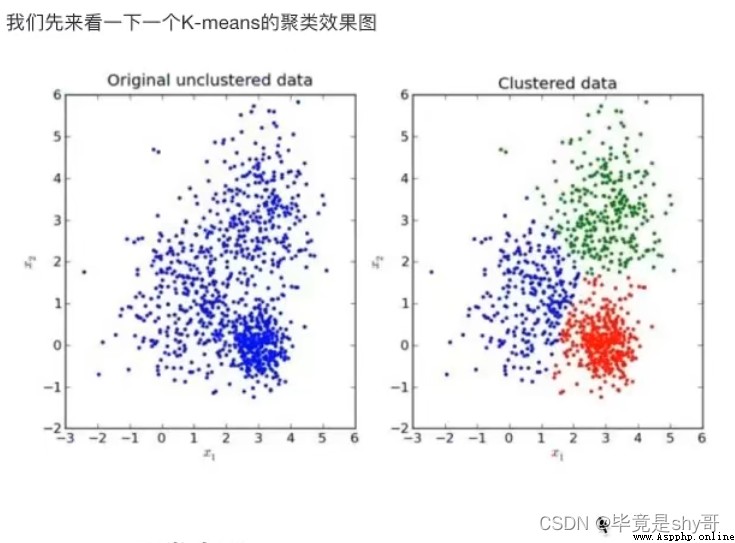
沒有目標值 - 無監督學習

4.6.2 無監督學習包含算法

• 聚類
  K-means(K均值聚類)
• 降維
  PCA

4.6.3 K-means原理

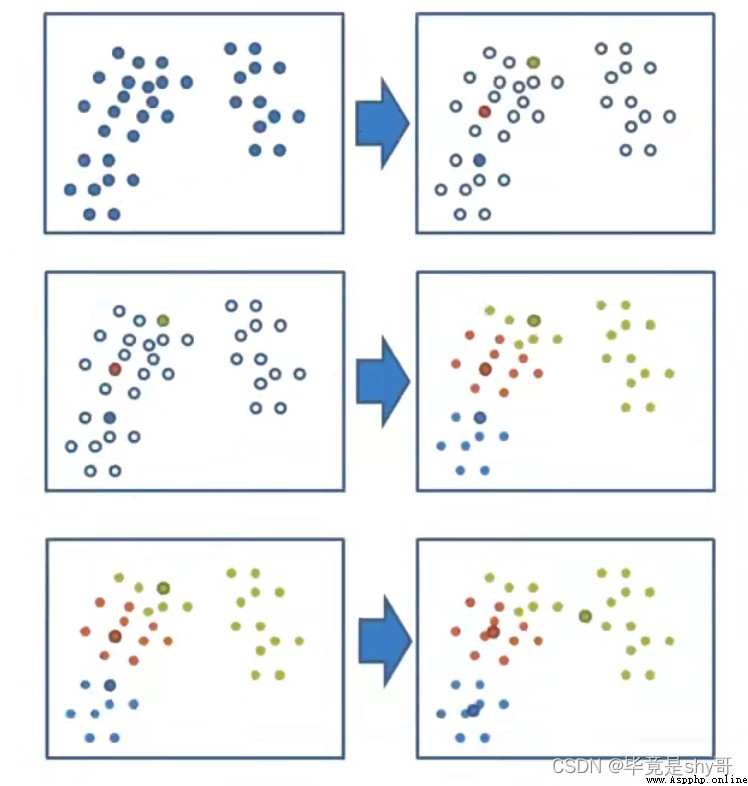
K-超參數
1看需求
2調節參數

4.6.4 API

4.6.5 案例：k-means對Instacart Market用戶聚類

k = 3
流程分析：
降維之後的數據
1）預估器流程
2）看結果
3）模型評估

4.6.6 Kmeans性能評估指標

輪廓系數
如果b_i>>a_i:趨近於1效果越好，
b_i<<a_i:趨近於-1，效果不好。
輪廓系數的值是介於 [-1,1] ，
越趨近於1代表內聚度和分離度都相對較優。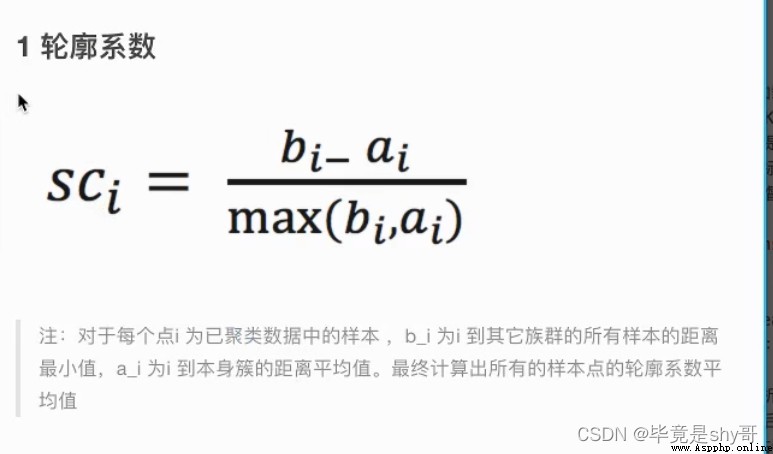

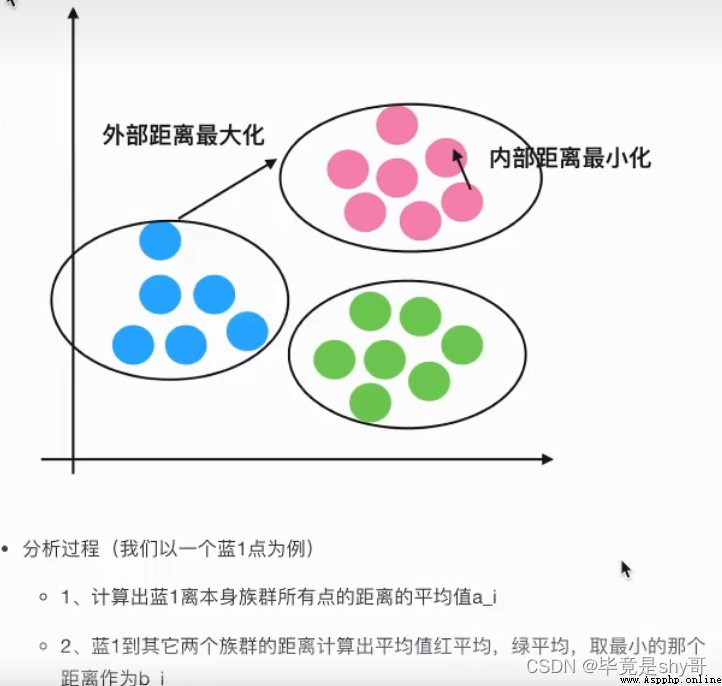
4.6.7 K-means總結

應用場景：
沒有目標值
分類