目錄

• 十大排序算法匯總
• list自帶排序
• • 一維
  • 二維
  • • 方法一：key = 自定義函數
    • 方法二：key = lambda 函數
    • 方法三：functools.cmp_to_key
    • • 單寫cmp函數
      • 用lambda函數
• dic 自帶排序
• 快速排序
• 堆排序
• 歸並排序
• • 歸並排序在鏈表排序中的應用
  • 歸並排序在合並多個鏈表上的應用
  • 歸並排序在統計逆序對上的應用
• 另外一道排序題

十大排序算法匯總

list自帶排序

一維

reverse = True 降序， reverse = False 升序（默認）
不需要返回值，nums就可以被修改

nums.sort(reverse = True)

l = sorted(l, reverse = True)

二維

方法一：key = 自定義函數

菜鳥教程上的例子：
按第二個元素排序

def takeSecond(elem):
return elem[1]
# 列表
random = [(2, 2), (3, 4), (4, 1), (1, 3)]
# 指定第二個元素排序
random.sort(key = takeSecond)

方法二：key = lambda 函數

[key,value]，先按value從大到小排，value相同時按key從小到大排。下面的兩種寫法都可以：

l.sort(key = lambda x:(-x[1],x[0])) # 默認從小到大，從大到小的話要加負號

l = sorted(l, key = lambda x:(-x[1],x[0]))

方法三：functools.cmp_to_key

在力扣179題裡，需要判斷兩個數字的字符串加起來誰大，就把誰排前面。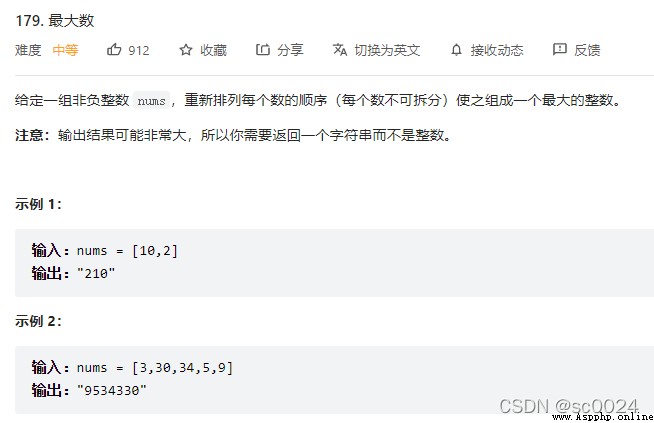

有兩種方法：

單寫cmp函數

class Solution:
def largestNumber(self, nums: List[int]) -> str:
strs = map(str, nums)
def cmp(a, b):
if a + b == b + a:
return 0
elif a + b > b + a:
return 1 # a在前面
else:
return -1
strs = sorted(strs, key=functools.cmp_to_key(cmp), reverse=True)
return ''.join(strs) if strs[0] != '0' else '0'

用lambda函數

from functools import cmp_to_key
class Solution:
def largestNumber(self, nums: List[int]) -> str:
strs = map(str, nums)
strs = sorted(strs, key = cmp_to_key(lambda x,y: int(x + y) - int(y + x)), reverse=True)
return ''.join(strs) if strs[0] != '0' else '0'

dic 自帶排序

和上面同樣的題目，用字典存儲鍵值對可以這樣排序：

dic = sorted(dic.items(), key=lambda x: (-x[1], x[0])) # 這樣可以

要注意dic.items()才是可迭代對象，而且dic沒有dic.sort()這種方法。
這樣排序之後dic會變成一個tuple的list，而不再是字典。

快速排序

最近在刷力扣，一開始想背個模板：

class Solution:
def sortArray(self, nums: List[int]) -> List[int]:
def quick_sort(arr,l,r):
i,j = l,r
if l>=r:
return
while i<j:
while i<j and arr[j]>=arr[l]:#取第一個元素為哨兵
j -= 1
while i<j and arr[i]<=arr[l]:
i += 1
arr[i], arr[j] = arr[j],arr[i]
#退出這個while循環時，i=j即從左右兩邊向中間相遇
arr[i],arr[l] = arr[l], arr[i] #pivot和相遇點交換
quick_sort(arr,l,i-1) # 遞歸地快排左右子數組
quick_sort(arr,i+1,r)
quick_sort(nums,0,len(nums)-1)
return nums

當我們討論時間復雜度，是對於任何測試用例取平均的一個概念，但具體時間會隨著測試用例的不同有一些差異。取第一個元素為哨兵從原則上沒有什麼問題，但是力扣有一個測試用例是長度為50000的本來就是升序的數組，在這種情況下，哪怕數組本來就是排好序的，while循環裡還是要一個個判斷，會超時，因此可以進行一些優化，也就是隨機取哨兵，這樣對不同排序程度的數組，運行時間的差距會更小一些。

注意有兩處代碼是和取arr[start]為哨兵不同的。

class Solution:
def sortArray(self, nums: List[int]) -> List[int]:
def quickSort(arr, start, end):
if start >= end:
return
index = random.randint(start, end)
pivot = arr[index] #隨機取哨兵
# 把隨機取的哨兵換到開頭的位置上，這樣就和上面的代碼幾乎一樣了
arr[start],arr[index] = arr[index],arr[start]
i, j = start, end
while i<j:
while i<j and arr[j]>=pivot:
j -= 1
while i<j and arr[i]<=pivot:
i += 1
if i != j:
arr[i],arr[j] = arr[j],arr[i]
arr[start], arr[i] = arr[i], arr[start] #哨兵和相遇點交換
quickSort(arr, start, i-1)
quickSort(arr, i+1, end)
quickSort(nums, 0, len(nums)-1)
return nums

堆排序

先上個模板，堆排序我看的是b站的視頻：堆排序視頻 圖是從視頻裡截的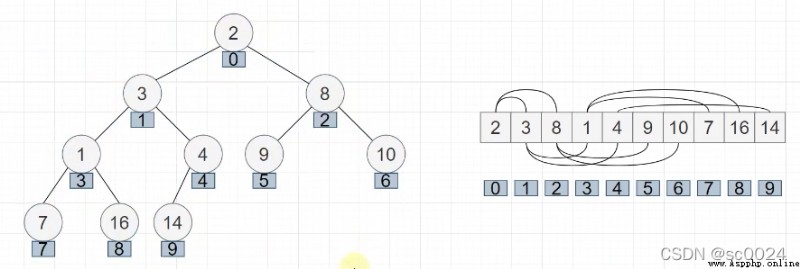

以升序排序為例，總的思路是，先把所有數組建堆，再每次從大根堆裡pop一個元素放到數組的最後面，然後更新堆以保持大根堆的性質。

建堆相當於初始化。注意建堆的時候是從第一個有葉子節點的元素開始，即圖裡的下標為4的元素。這個4是怎麼得到的呢？是根據數組的總長度算出來的。從後往前，第一個有葉子節點的元素下標是len(nums) - 1) // 2（當然前提是索引從0開始）。

開始取元素的時候，每次從堆頂取一個元素放到nums的最後面，把本來在最後面的元素換到堆頂去，然後更新堆以維護它的性質。

class Solution:
def max_heapify(self, heap, n,i):
# n 是要處理的數組長度
# i 是當前索引
largest = i
left, right = 2*i+1, 2*i+2
if left<n and heap[largest]<heap[left]: # 如果左孩子更大
largest = left
if right<n and heap[largest]<heap[right]: # 如果右孩子更大
largest = right
if largest != i:
heap[largest], heap[i] = heap[i], heap[largest]
self.max_heapify(heap,n,largest) # 遞歸
def heap_sort(self, nums):
# 建堆
for i in range((len(nums) - 1)//2, -1, -1):
self.max_heapify(nums, len(nums), i)
# 每次用堆頂元素和未排序的最後一個元素交換
for i in range(len(nums) - 1, -1, -1):
nums[i], nums[0] = nums[0], nums[i]
self.max_heapify(nums, i,0)
def sortArray(self, nums: List[int]) -> List[int]:
self.heap_sort(nums)
return nums

python自帶的heapq用法，見鏈接，默認是小根堆

import heapq
#使數組轉化為堆
heap = [1,3,4,2,6,8,9]
heapq.heapify(heap)
# heap = [1,2,4,3,6,8,9]
#為heap增加元素
heap = [1,3,4,2,6,8,9]
heapq.heappush(heap, 2)
# heap = [1,3,4,2,6,8,9,2]
#刪除堆頂（即最小值）
heap = [1,3,4,2,6,8,9]
heapq.heappop(heap)
# heap = [3,2,4,9,6,8] #刪除堆頂後將堆尾放到堆頂，然後下沉
#查堆中最大n個數
heap = [1,3,4,2,6,8,9]
result = heapq.nlargest (2, heap)
# result = [9,8]
#查堆中最小n個數
heap = [1,3,4,2,6,8,9]
result = heapq.nsmallest (2, heap)
# result = [1,2]

歸並排序

同樣參考這個up的另一個視頻：歸並排序視頻
思路就是先遞歸地把數組從中間二分成很多小段，然後按順序合並。注意最後要把合並後的數組拷回原來的數組。

class Solution:
def merge_sort(self, nums, l, r):
if l == r:
return
mid = (l + r) // 2
self.merge_sort(nums, l, mid)
self.merge_sort(nums, mid + 1, r)
self.merge(nums,l,mid,r)
def merge(self,nums,left,mid,right):
l = left
r = mid+1
tmp = []
while l<=mid and r<=right:
if nums[l] < nums[r]: #左半區第一個剩余元素更小
tmp.append(nums[l])
l += 1
else:
tmp.append(nums[r])
r += 1
# 右半區用完了，左半區直接搬過去
if l<=mid:
tmp.extend(nums[l:mid+1])
# 左半區用完了，右半區直接搬過去
if r<=right:
tmp.extend(nums[r:right+1])
# 把合並後的數組拷回原來的數組
nums[left:right+1] = tmp

歸並排序在鏈表排序中的應用

148. 排序鏈表

class Solution:
def sortList(self, head: ListNode) -> ListNode:
# 注意二分鏈表的遞歸終止條件
if not head or not head.next:
return head
# 計算中點並分割
mid = self.splitList(head)
# 遞歸調用
left = self.sortList(head)
right = self.sortList(mid)
return self.merge_list(left,right)
def splitList(self,head):
# 用快慢指針找到鏈表的中點
slow = head
fast = head.next
while fast and fast.next:
slow = slow.next # slow一次走一步
fast = fast.next.next # fast一次走兩步
tmp = slow.next
slow.next = None
return tmp
def merge_list(self,head1,head2):
# 合並兩個鏈表
dummyhead = ListNode()
head = dummyhead
while head1 and head2:
if head1.val<head2.val:
head.next, head1 = head1, head1.next
else:
head.next, head2 = head2, head2.next
head = head.next
head.next = head1 if head1 else head2
return dummyhead.next

歸並排序在合並多個鏈表上的應用

23. 合並K個升序鏈表
分治解法應該是最優的，時間復雜度為 O ( k n ∗ l o g k ) O(kn*logk) O(kn∗logk)，空間復雜度為 O ( l o g k ) O(logk) O(logk)

class Solution:
def mergeKLists(self, lists: List[ListNode]) -> ListNode:
if not lists:
return
n = len(lists)
return self.merge(lists, 0, n-1)
def merge(self,lists, left, right):
# left 和 right 只是左右區間的下標
if left == right:
return lists[left]
mid = left + (right - left) // 2
#遞歸二分
l1 = self.merge(lists, left, mid) #左半區合並完的鏈表
l2 = self.merge(lists, mid+1, right) #右半區合並完的鏈表
return self.mergeTwoLists(l1, l2)
def mergeTwoLists(self,head1,head2):
# 合並兩個鏈表
dummyhead = ListNode()
head = dummyhead
while head1 and head2:
if head1.val<head2.val:
head.next, head1 = head1, head1.next
else:
head.next, head2 = head2, head2.next
# 以head.next = head1結束時，head指向倒數第二個元素
head = head.next #將head移到鏈表尾
head.next = head1 if head1 else head2
return dummyhead.next

歸並排序在統計逆序對上的應用

劍指 Offer 51. 數組中的逆序對

class Solution:
def reversePairs(self, nums: List[int]) -> int:
def merge_sort(l, r):
# 終止條件
if l >= r:
return 0
# 遞歸劃分
m = (l + r) // 2
res = merge_sort(l, m) + merge_sort(m + 1, r)
# 合並階段
i, j = l, m + 1 # 左右子數組的起點
tmp[l:r + 1] = nums[l:r + 1] # tmp用來暫存有序數組
for k in range(l, r + 1):
# 左數組合並完，放右數組的值
if i == m + 1:
nums[k] = tmp[j]
j += 1
# 右數組合並完，或左數組當前值較小，兩種情況都往tmp中放左數組的值
elif j == r + 1 or tmp[i] <= tmp[j]:
nums[k] = tmp[i]
i += 1
# 左數組當前值較大，左數組的每一個元素-右數組當前元素，都能組成一個逆序對
else:
nums[k] = tmp[j]
j += 1
res += m - i + 1 # 統計逆序對
# 注意res並沒有初始化過
return res
tmp = [0] * len(nums)
return merge_sort(0, len(nums) - 1)

另外一道排序題

581. 最短無序連續子數組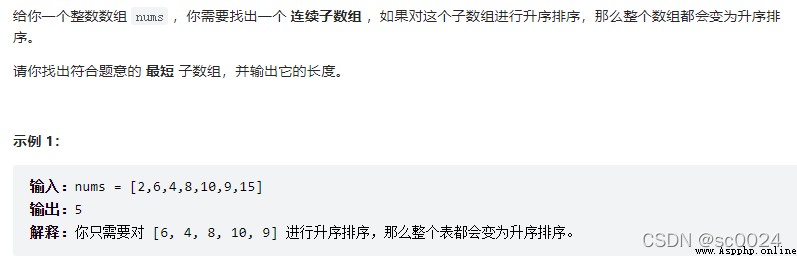

思路是用排序的數組和不排序的數組比，看中間哪段不一樣，取出那段的左右坐標，就是答案
left 從左往右找，right 從右往左找
如果數組本來就是升序，left會到數組的最後一個位置，right會到0，right-left+1是負數，所以最後用max()函數判斷。

class Solution:
def findUnsortedSubarray(self, nums: List[int]) -> int:
sorted_nums = sorted(nums)
left = 0
while left<len(nums) and sorted_nums[left] == nums[left]:
left += 1
right = len(nums)-1
while right>=0 and sorted_nums[right] == nums[right]:
right -= 1
return max(0, right-left+1)