基於python的對比度增強(線性變換、直方圖正規化、直方圖均衡化、CLAHE)

線性變換

假設輸入圖像為I，寬為W，高為H，輸出圖像為O，圖像的線性變換可以用以下公式定義:
O ( r , c ) = a × I ( r , c ) + b , 0 ≤ r < H , 0 ≤ c < W O(r, c) = a × I(r, c) + b, 0 ≤ r < H, 0 ≤ c < W O(r,c)=a×I(r,c)+b,0≤r<H,0≤c<W
當a=1，b=0時，O為I的一個副本；如果a>1，則輸出圖像O的對比度比I有所增大；如果0<a<1，則O的對比度比I有所減小。而b值的改變，影響的是輸出圖像的亮度，當b>0時，亮度增加；當b<0時，亮度減小

import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt
# 統計灰度直方圖並繪制
def calGrayHist(I):
h, w = I.shape
grayHist = np.zeros(256, np.uint64)
for i in range(h):
for j in range(w):
grayHist[I[i][j]] += 1
plt.plot(grayHist)
plt.xlabel("gray label")
plt.ylabel("number of pixels")
img_gray = cv.imread("./001_07.bmp", 0)
out = 2.0 * img_gray + 5
# 進行數據截斷，大於255的像素值截斷為255
out[out > 255] = 255
out = out.astype(np.uint8)
plt.figure(figsize=(20,5))
plt.subplot(141)
plt.imshow(img_gray, cmap = "gray")
plt.subplot(142)
calGrayHist(img_gray)
plt.subplot(143)
plt.imshow(out, cmap = "gray")
plt.subplot(144)
calGrayHist(out)
# plt.savefig("./showimg.jpg")
plt.show()

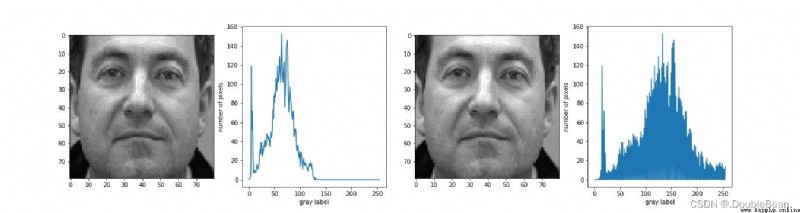
線性變換的參數需要根據不同的應用及圖像自身的信息進行合理的選擇，可能需要進行多次測試，所以選擇合適的參數是相當麻煩的。直方圖正規化就是基於當前圖像情況自動選取a和b的值的方法

直方圖正規化

# 直方圖正規化
# 計算原圖中出現的最小灰度級和最大灰度級
Imin, Imax = cv.minMaxLoc(img_gray)[:2]
''' # 也可以使用numpy計算 Imax = np.max(img_gray) Imin = np.min(img_gray) '''
Omin, Omax = 0, 255
a = float(Omax - Omin) / (Imax - Imin)
b = Omin - a * Imin
out = a * img_gray + b
out = out.astype(np.uint8)

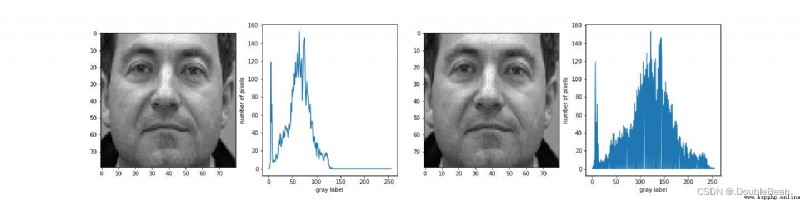
代碼中計算原圖中出現的最小灰度級和最大灰度級可以使用OpenCV提供的函數

minVal, maxVal, minLoc, maxLoc = cv.minMaxLoc(src[, mask])

返回值分別為：最小值，最大值，最小值的位置索引，最大值的位置索引。

正規化函數normalize:dst=cv.normalize(src, dst[, alpha[, beta[, norm_type[, dtype[, mask]]]]])

使用函數normalize對圖像進行對比度增強時，經常令參數norm_type=NORM_MINMAX，此函數內部實現和上邊講的計算方法是相同的，參數alpha相當於O_max，參數beta相當於O_min。注意，使用normalize可以處理多通道矩陣，分別對每一個通道進行正規化操作。使用該函數的代碼如下，實現結果和上邊是相同的

out = np.zeros(img_gray.shape, np.uint8)
cv.normalize(img_gray, out, 255, 0, cv.NORM_MINMAX, cv.CV_8U) # 調庫
cv.imshow("img", img)
cv.imshow("out", out)
cv.waitKey(0)
cv.destroyAllWindows()

直方圖均衡化(Histogram Equalization)

直方圖均衡化是指: 利用圖像直方圖對對比度進行調整的方法
直方圖均衡化通常用來增加許多圖像的局部對比度，尤其是當圖像的有用數據的對比度相當接近的時候
為討論方便起見，以 r 和 s 分別表示歸一化了的原圖像灰度和經直方圖均衡化後的圖像灰度。當 r = s = 0 時，表示黑色；當 r = s = 1 時，表示白色；當 r, s ∈ (0, 1) 時，表示像素灰度在黑白之間變化
在 [0,1] 區間內的任何一個 r ，經變換函數 T ( r ) T(r) T(r) 都可以產生一個對應的 s
s = T ( r ) s = T(r) s=T(r)
式中， T ( r ) T(r) T(r) 應當滿足以下兩個條件:

1. 在 0 ≤ r ≤ 1 內， T ( r ) T(r) T(r) 為單調遞增函數；(此條件保證了均衡化後圖像的灰度級從黑到白的次序不變)
2. 在 0 ≤ r ≤ 1 內有 0 ≤ T ( r ) ≤ 1 0 ≤ T(r) ≤ 1 0≤T(r)≤1。(此條件保證了均衡化後圖像的像素灰度值在允許的范圍內)

如果已知隨機變量 r 的概率密度是 p r ( r ) p_{r}(r) pr​(r)，而隨機變量 s 是 r 的函數，則 s 的概率密度 p s ( s ) p_{s}(s) ps​(s) 可以由 p r ( r ) p_{r}(r) pr​(r) 求出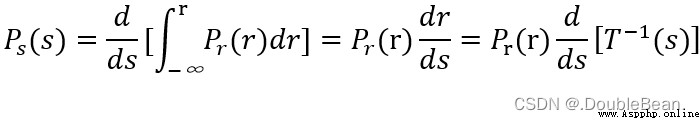

則有: p s ( s ) d s = p r ( r ) d r p_{s}(s)ds = p_{r}(r)dr ps​(s)ds=pr​(r)dr
又有：從人眼視覺特性來考慮，一幅圖像的灰度直方圖如果是均勻分布的，那麼該圖像看上去效果比較好 (參考岡薩雷斯數字圖像處理3.3節)。因此要做直方圖均衡化，這裡的 p s ( s ) p_{s}(s) ps​(s) 應當是均勻分布的概率密度函數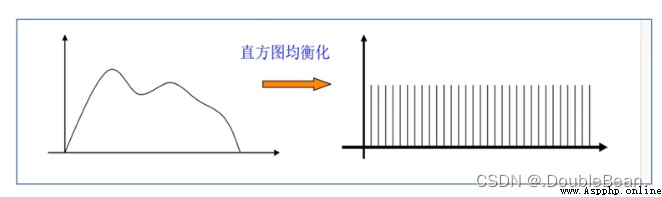

由概率論知識可知，對於區間 [a,b] 上的均勻分布，其概率密度函數等於 1 b − a \frac{1}{b-a} b−a1​。 如果原圖像沒有進行歸一化，即 r ∈ [ 0 , L − 1 ] r \in [0, L-1] r∈[0,L−1], 那麼 p s ( s ) = 1 ( L − 1 ) − 0 = 1 L − 1 p_{s}(s) = \frac{1}{(L-1)-0} = \frac{1}{L-1} ps​(s)=(L−1)−01​=L−11​，歸一化之後 r ∈ [ 0 , 1 ] r \in [0, 1] r∈[0,1]，所以這裡的 p s ( s ) = 1 1 − 0 = 1 p_{s}(s) = \frac{1}{1-0} = 1 ps​(s)=1−01​=1

將 p s ( s ) = 1 p_{s}(s) = 1 ps​(s)=1代入上式有: d s = p r ( r ) d r ds = p_{r}(r)dr ds=pr​(r)dr，
兩邊積分得: s = T ( r ) = ∫ 0 r p r ( r ) d r s = T(r) = \int_{0}^{r}p_{r}(r)dr s=T(r)=∫0r​pr​(r)dr
由於數字圖像灰度級是離散的，所以推廣到離散情況，即用頻率代替概率，有:
s k = T ( r k ) = ∑ i = 0 k p r ( r i ) = ∑ i = 0 k n i N s_{k} = T(r_{k}) = \sum_{i=0}^{k}p_{r}(r_{i}) = \sum_{i=0}^{k}\frac{n_{i}}{N} sk​=T(rk​)=i=0∑k​pr​(ri​)=i=0∑k​Nni​​
式中， 0 ⩽ r k ⩽ 1 , k = 0 , 1 , 2 , . . . , L − 1 0 \leqslant r_{k} \leqslant 1, k = 0, 1, 2, ..., L-1 0⩽rk​⩽1,k=0,1,2,...,L−1 (注: 這裡的 r k = k L − 1 r_{k} = \frac{k}{L-1} rk​=L−1k​，表示歸一化後的灰度級；k表示歸一化前的灰度級)，而且需要注意的是，這裡的 s k s_{k} sk​ 也是歸一化後的灰度級，其值在 0 到 1 之間；有時需要將其乘以L-1再取整，使其灰度級范圍在 0 到 L-1 之間，與原圖像一致

# 全局直方圖均衡化
def equalHist(img, z_max = 255): # z_max = L-1 = 255
# 灰度圖像矩陣的高、寬
H, W = img.shape
# S is the total of pixels
S = H * W
out = np.zeros(img.shape)
sum_h = 0
for i in range(256):
ind = np.where(img == i)
sum_h += len(img[ind])
z_prime = z_max / S * sum_h
out[ind] = z_prime
out = out.astype(np.uint8)
return out

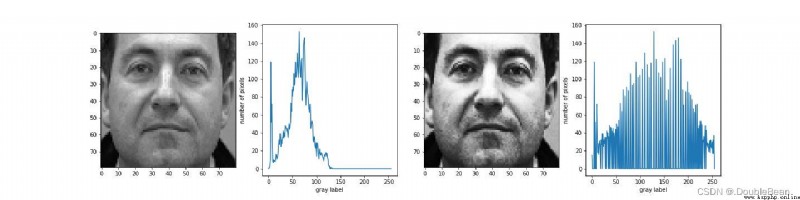
從結果圖的直方圖分布來看，並不是理想的一條水平線，原因是我們是在連續分布上推導得到的轉換函數，但作用於離散分布，且不允許出現非整數形式的新結果
不過，整體看來該轉換函數使得新的分布具有展開直方圖分布的效果，增強了整體的對比度

限制對比度的自適應直方圖均衡化(CLAHE)

關於CLAHE原理講解的大多數文章講的都很泛，就像蜻蜓點水般隨便扯一下就直接調庫實現了，所以真要弄懂的話還是要看源碼
http://www.realtimerendering.com/resources/GraphicsGems/gemsiv/clahe.c

上述HE算法得到的結果存在一些問題: 1) 部分區域由於對比度增強過大，成為噪點；2) 一些區域調整後變得更暗/更亮，丟失細節信息

針對問題1)，有人提出了CLHE (即 Contrast Limited HE對比度限制的HE算法)
對統計得到的直方圖進行裁剪，使其幅值低於某個上限，將裁剪掉的部分均勻分布在整個灰度區間，以確保直方圖總面積不變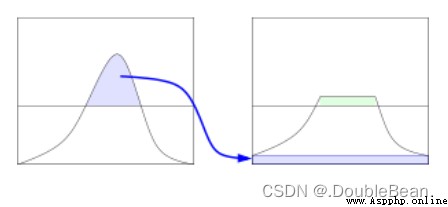

可以看到，這時直方圖又會整體上升了一個高度，會超過我們設置的上限
其實在具體實現的時候有很多解決方法，可以多重復幾次裁剪過程，使得上升的部分變得微不足道，或是用另一種常用的方法:

• 設裁剪值為ClipThreshold，求直方圖中高於該阈值的部分的總和totalExcess，此時如果把totalExcess均分給所有灰度級，那麼最終的直方圖整體會上升一個高度，這個高度是averageIncrease = totalExcess / N，以upper = ClipThreshold - averageIncrease為界限對直方圖進行如下處理:
  1.若幅值高於ClipThreshold，直接設置為ClipThreshold
  2.若幅值處於upper和ClipThreshold之間，從totalExcess中取出ClipThreshold - 幅值，將幅值填補成ClipThreshold
  3.若幅值低於upper，直接加上averageIncrease即可
  
• 實現完上面的操作後，還有一些剩余的totalExcess沒有被分出去，這個剩余是來自於1.和2.，這時需要再把這些均勻分給那些目前幅值依舊低於ClipThreshold的灰度值

''' This function performs clipping of the histogram and redistribution of bins. The histogram is clipped and the number of excess pixels is counted. Afterwards the excess pixels are equally redistributed across the whole histogram (providing the bin count is smaller than the cliplimit). '''
def ClipHistogram(pHistogram, ClipThreshold):
totalExcess = 0
# 累計超出阈值的部分
for i in range(256):
if pHistogram[i] > ClipThreshold:
totalExcess += (pHistogram[i] - ClipThreshold)
averageIncrease = totalExcess // 256
upper = ClipThreshold - averageIncrease
# 修剪直方圖並重新分配數值
for i in range(256):
if pHistogram[i] >= ClipThreshold: # 幅值高於ClipThreshold
pHistogram[i] = ClipThreshold
else:
if pHistogram[i] > upper: # 幅值介於upper和ClipThreshold之間
totalExcess -= (ClipThreshold - pHistogram[i])
pHistogram[i] = ClipThreshold
else: # 幅值小於upper
totalExcess -= averageIncrease
pHistogram[i] += averageIncrease
pStartBin = 0
while totalExcess > 0:
# 上述過程後totalExcess仍會有剩余未分配，設置步長將剩余的進行均分
step_size = int(256 / totalExcess)
if step_size < 1: # step_size至少為1
step_size = 1
for i in range(pStartBin, 256, step_size):
if totalExcess == 0:
break
if pHistogram[i] < ClipThreshold:
pHistogram[i] += 1
totalExcess -= 1 # 減少totalExcess
pStartBin += 1 # 在其他位置重新開始分配
return pHistogram

針對問題2)，有人提出AHE (Adaptive HE自適應直方圖均衡化算法)，基本思想是: 對原圖中每個像素，計算其周圍一個鄰域內的直方圖，並使用HE映射得到新的像素值。為了能夠處理圖像邊緣的像素，一般先對原始圖像做鏡像擴邊處理
不過這樣做計算量偏大，為了減少計算量，一般先把原始圖像分塊，分別對每個子區域進行HE變換。但是這樣又產生了新的問題，子區域相接處像素值分布不連續，產生很強的分割線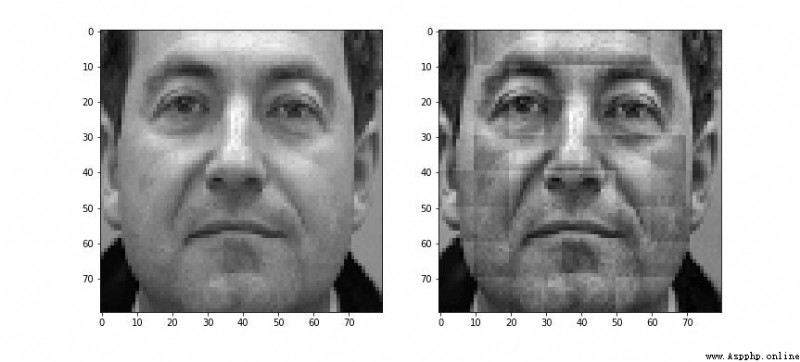

為了解決這個問題，提出了優化方案雙線性插值的AHE，然後在這個基礎上，再使用CLHE的限制對比度的思想，就變成了我們熟知的CLAHE算法

CLAHE算法的步驟:

1. 圖像分塊，以塊為單位，統計子塊的直方圖
2. 使用限制對比度方法進行修剪直方圖，最後再直方圖均衡化
3. 像素點灰度值重構，使用的是雙線性插值

【雙線性插值】
對圖像分塊，然後對每一塊求直方圖均衡化，但不是把直方圖均衡化的結果全部賦給這個子塊，因為這樣會造成塊跟塊之間像素值不連續
那像素點的灰度級該如何更新? 根據像素點所在位置分成三類
在粉色區域內的點的灰度就等於直方圖均衡化的結果，即直接由映射函數計算得到
在綠色區域內的點的灰度由相鄰兩個子圖映射函數插值得到
在其他區域內的所有點的灰度由相鄰四個子圖映射函數雙線性插值得到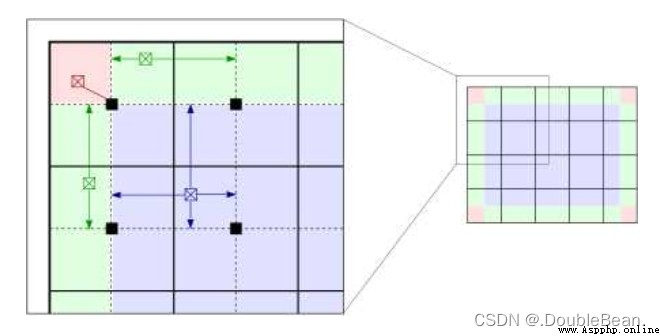

如下圖所示便是雙線性插值的情況，O點的灰度值為 r o r_o ro​，對其周圍最近的四個子塊的灰度映射函數進行雙線性插值的結果為:
s o = ( 1 − x ) ( 1 − y ) T A ( r o ) + x ( 1 − y ) T B ( r o ) + ( 1 − x ) y T C ( r o ) + x y T D ( r o ) s_o = (1 - x)(1 - y)T_A(r_o) + x(1 - y)T_B(r_o) + (1 - x)yT_C(r_o) + xyT_D(r_o) so​=(1−x)(1−y)TA​(ro​)+x(1−y)TB​(ro​)+(1−x)yTC​(ro​)+xyTD​(ro​)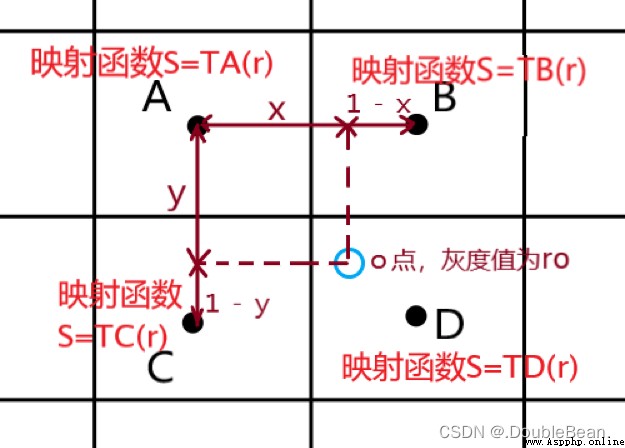

【線性插值代碼實現中的細節】
舉個例子:
把一張圖片分成4×3個子圖，每個格子為4×4大小，圖中的P、Q兩點位於邊界處，所以需要使用線性插值得到這兩個點的灰度級，線性插值第一步找到該點周圍相鄰的兩個子圖，那P點和Q點的相鄰子圖分別是什麼？假設P點坐標為(11, 2)、Q點坐標為(9, 2)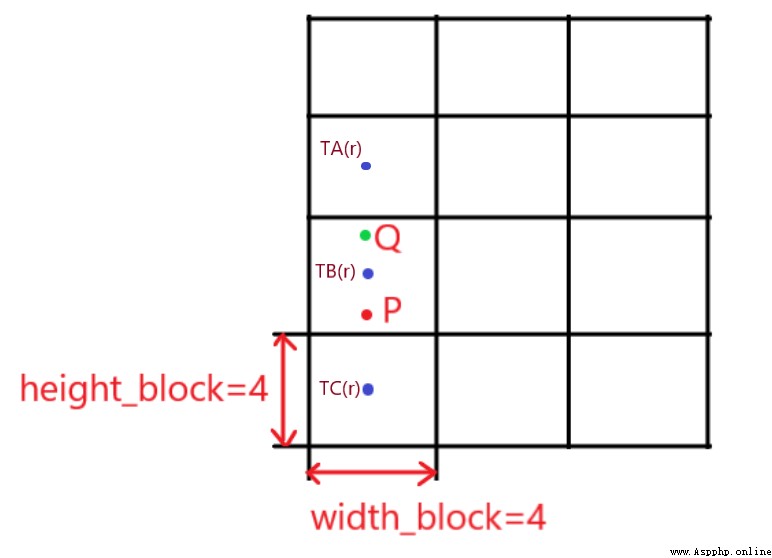

可以看到，雖然P點和Q點在同一個子圖中，但相鄰子圖是不同的，Q點的灰度級是由 T A ( r ) T_A(r) TA​(r)和 T B ( r ) T_B(r) TB​(r)這兩個映射函數得到，也就是說Q點相鄰的兩個子圖是第3個和第6個子圖(從0開始編號)，而P點的灰度級是由 T B ( r ) T_B(r) TB​(r)和 T C ( r ) T_C(r) TC​(r)這兩個映射函數得到，是第6個子圖和第9個子圖
代碼中如何判定？

Q = (9, 2)
P = (11, 2)
tileGridSize = (4, 3) # 將圖片分成4×3份
height_block, width_block = 4, 4 # 每個子圖的大小
Q_numi = int((Q[0] - height_block / 2) / height_block)
Q_num1 = Q_numi * tileGridSize[1]
Q_num2 = Q_num1 + tileGridSize[1]
P_numi = int((P[0] - height_block / 2) / height_block)
P_num1 = P_numi * tileGridSize[1]
P_num2 = P_num1 + tileGridSize[1]
print(Q_num1, Q_num2)
print(P_num1, P_num2)

運行結果為:

3 6
6 9

Q點的灰度級公式就為:
s Q = ( 1 − y Q ) T A ( r Q ) + y Q T B ( r Q ) s_Q = (1 - y_Q)T_A(r_Q) + y_QT_B(r_Q) sQ​=(1−yQ​)TA​(rQ​)+yQ​TB​(rQ​)
P點的灰度級公式就為:
s P = ( 1 − y P ) T B ( r P ) + y P T C ( r P ) s_P = (1 - y_P)T_B(r_P) + y_PT_C(r_P) sP​=(1−yP​)TB​(rP​)+yP​TC​(rP​)
問題來了: y_Q和y_P怎麼獲得？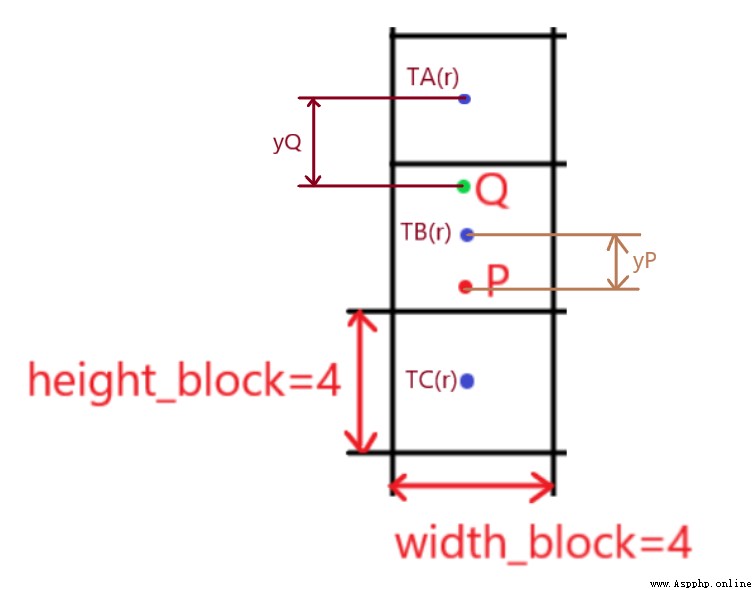

從上圖來看，無非就是該點到相鄰的第一個子圖中心的距離，所以我們需要知道第一個子圖中心位置，Q點相鄰的第一個子圖中心坐標為(6, 2)，P點相鄰的第一個子圖中心坐標為(10, 2)

print(Q_numi * height_block + height_block / 2)
print(P_numi * height_block + height_block / 2)
yQ = (Q[0] - (Q_numi * height_block + height_block / 2)) / height_block
yP = (P[0] - (P_numi * height_block + height_block / 2)) / height_block # 除以height_block是為了歸一化
print(yQ)
print(yP)

代碼運行結果:

6.0
10.0
0.75
0.25

當然，應該也可以使用另一種方式求y_Q和y_P，但我不知道這個對不對，因為我剛開始是想著用求余的方式求y_Q和y_P，就推出了這個，和上面那種方法求出來的結果是一樣的

yQ = (Q[0] - height_block / 2) % height_block / height_block
yP = (P[0] - height_block / 2) % height_block / height_block
print(yQ)
print(yP)

CLAHE代碼:

def my_CLAHE(img, clipLimit, tileGridSize):
height, width = img.shape
height_block = height // tileGridSize[0]
width_block = width // tileGridSize[1]
total = width_block * height_block
average = width_block * height_block / 256
ClipThreshold = int(clipLimit * average)
multi_cdf = []
for i in range(tileGridSize[0]):
for j in range(tileGridSize[1]):
grid = img[i*height_block : (i+1)*height_block, j*width_block : (j+1)*width_block]
hist = calGrayHist(grid) # 統計每個子塊的直方圖
hist = ClipHistogram(hist, ClipThreshold) # 限制對比度對直方圖進行修剪
# 獲取累計分布直方圖cdf
cdf = np.zeros(256)
for k in range(256):
if k == 0:
cdf[k] = hist[k] / total
else:
cdf[k] = cdf[k-1] + (hist[k] / total)
multi_cdf.append(cdf.tolist())
print(np.array(multi_cdf).shape)
out = np.zeros(img.shape)
# 計算CLAHE後的像素值: 根據像素點的位置，選擇不同的計算方法
for i in range(height):
for j in range(width):
# four coners，即紅色區域，灰度級直接由映射函數計算得到
if i <= height_block / 2 and j <= width_block / 2: # 左上角
num = 0
out[i][j] = int(multi_cdf[num][img[i][j]] * 255)
elif i <= height_block / 2 and j >= ((tileGridSize[1] - 1) * width_block + width_block / 2): # 右上角
num = tileGridSize[1] -1
out[i][j] = int(multi_cdf[num][img[i][j]] * 255)
elif i >= ((tileGridSize[0] - 1) * height_block + height_block / 2) and j <= width_block: # 左下角
num = tileGridSize[1] * (tileGridSize[0] - 1)
out[i][j] = int(multi_cdf[num][img[i][j]] * 255)
elif i >= ((tileGridSize[0] - 1) * height_block + height_block / 2) and j >= ((tileGridSize[1] - 1) * width_block + width_block / 2): # 右下角
num = tileGridSize[0] * tileGridSize[1] - 1
out[i][j] = int(multi_cdf[num][img[i][j]] * 255)
# four edges except coners，即綠色區域，灰度級由線性插值得到
elif j <= width_block / 2: # 左邊界
num_i = int((i - height_block / 2) / height_block)
num1 = num_i * tileGridSize[1]
num2 = num1 + tileGridSize[1]
y = (i - (num_i * height_block + height_block / 2)) / height_block # 歸一化
out[i][j] = int(((1 - y) * multi_cdf[num1][img[i][j]] + y * multi_cdf[num2][img[i][j]]) * 255)
elif i <= height_block / 2: # 上邊界
num_j = int((j - width_block / 2) / width_block)
num1 = num_j
num2 = num1 + 1
x = (j - (num_j * width_block + width_block / 2)) / width_block # 歸一化
out[i][j] = int(((1 - x) * multi_cdf[num1][img[i][j]] + x * multi_cdf[num2][img[i][j]]) * 255)
elif j >= ((tileGridSize[1] - 1) * width_block + width_block / 2): # 右邊界
num_i = int((i - height_block / 2) / height_block)
num1 = num_i * tileGridSize[1] + tileGridSize[1] - 1
num2 = num1 + tileGridSize[1]
y = (i - (num_i * height_block + height_block / 2)) / height_block # 歸一化
out[i][j] = int(((1 - y) * multi_cdf[num1][img[i][j]] + y * multi_cdf[num2][img[i][j]]) * 255)
elif i >= ((tileGridSize[0] - 1) * height_block + height_block / 2): # 下邊界
num_j = int((j - width_block / 2) / width_block)
num1 = num_j + (tileGridSize[0] - 1) * tileGridSize[1]
num2 = num1 + 1
x = (j - (num_j * width_block + width_block / 2)) / width_block # 歸一化
out[i][j] = int(((1 - x) * multi_cdf[num1][img[i][j]] + x * multi_cdf[num2][img[i][j]]) * 255)
# inner area，即紫色區域，灰度級由雙線性插值得到
else:
num_i = int((i - height_block / 2) / height_block)
num_j = int((j - width_block / 2) / width_block)
num1 = num_i * tileGridSize[1] + num_j
num2 = num1 + 1
num3 = num1 + tileGridSize[1]
num4 = num2 + tileGridSize[1]
x = (j - (num_j * width_block + width_block / 2)) / width_block # 歸一化
y = (i - (num_i * height_block + height_block / 2)) / height_block # 歸一化
out[i][j] = int(((1 - x) * (1 - y) * multi_cdf[num1][img[i][j]] +
x * (1- y) * multi_cdf[num2][img[i][j]] +
(1 - x) * y * multi_cdf[num3][img[i][j]] +
x * y * multi_cdf[num4][img[i][j]]) * 255)
out = out.astype(np.uint8)
return out

代碼運行結果: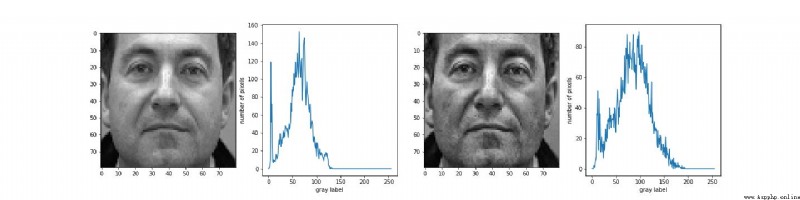

調庫實現

# 創建CLAHE對象
clahe = cv.createCLAHE(clipLimit=4.0, tileGridSize=(8, 8))
# 限制對比度的自適應阈值直方圖均衡化
img_gray_clahe = clahe.apply(img_gray)

我代碼中沒有考慮過如果圖像尺寸無法整除分塊大小的情況，貼上別人的博客吧，以後有時間再去想
OpenCV自適應直方圖均衡CLAHE圖像和分塊大小不能整除的處理

參考資源:

• 【圖像處理算法】直方圖均衡化
• 限制對比度自適應直方圖均衡(CLAHE算法)
• 直方圖均衡化(HE, AHE, CLAHE)
• 限制對比度自適應直方圖均衡化（自我理解）
• OpenCV–Python 圖像增強（線性變換，直方圖正規化，伽馬變換，全局直方圖均衡化，限制對比度的自適應直方圖均衡化）