深度學習
第一章 深度學習概述
一、引入
1. 人工智能劃時代事件
- 2016年3月,Google公司研發的AlphaGo以4:1擊敗世界圍棋頂級選手李世石。次年,AlphaGo2.0對戰世界最年輕的圍棋四冠王柯潔,以3:0擊敗對方,背後支撐AlphaGo具備如此強大能力的,就是“深度學習”(Deep Learning)。
- 一時間,“深度學習”這個本專屬於計算機學科的術語,成為包括學術界、工業界、風險投資界等眾多領域的熱詞。
2. 深度學習巨大影響
- 除了博弈,深度學習在計算機視覺(computer vision)、語音識別、自動駕駛等領域,表現與人類一樣好,甚至有些地方超過了人類。2013年,深度學習就被麻省理工學院的《MIT科技評論》評為世界10大突破性技術之一。
- 深度學習不僅是一種算法升級,還是一種全新的思維方式,它的顛覆性在於,將人類過去癡迷的算法問題,演變成數據和計算問題,以前“算法為核心競爭力”正在轉換為“數據為核心競爭力”。
二、深度學習的定義
1. 什麼是深度學習?
- 簡單來說,深度學習就是一種包括多個隱含層(越多即為越深)的多層感知機。它通過組合低層特征,形成更為抽象的高層表示,用以描述被識別對象的高級屬性類別或特征。能自生成數據的中間表示(雖然這個表示並不能被人類理解),是深度學習區別於其他機器學習算法的獨門絕技。
- 所以,深度學習可以總結成:通過加深網絡,提取數據深層次特征。
2. 深度神經網絡
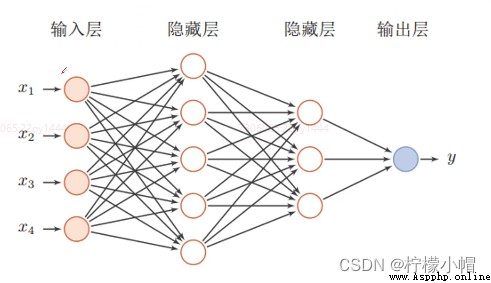
3. 深度學習與機器學習的關系
- 人工智能學科體系
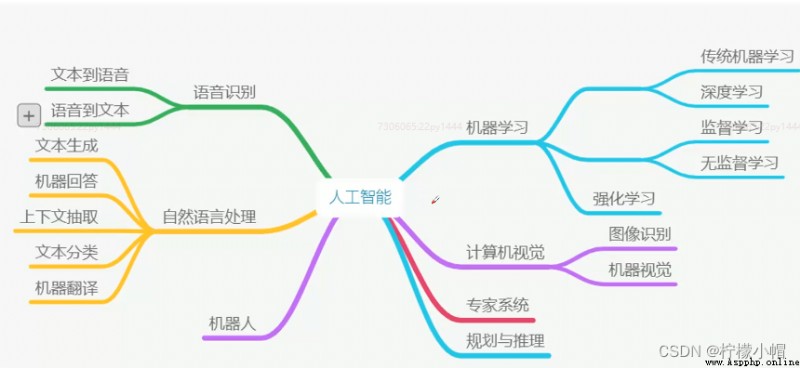
- 人工智能、機器學習、深度學習三者的關系,可以認為深度學習是機器學習的“高級階段“
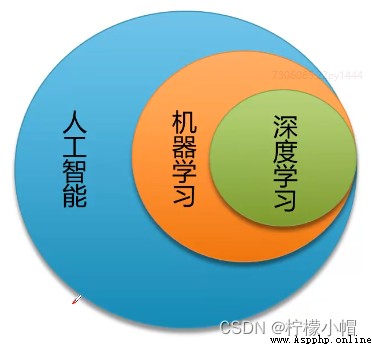
三、深度學習的特點
1. 深度學習的特點
- 優點:
- 性能更優異
- 不需要特征工程
- 在大數據樣本下有更好的性能
- 能解決某些傳統機器學習無法解決的問題
- 缺點:
2. 深度學習的優點
2.1 性能更優異
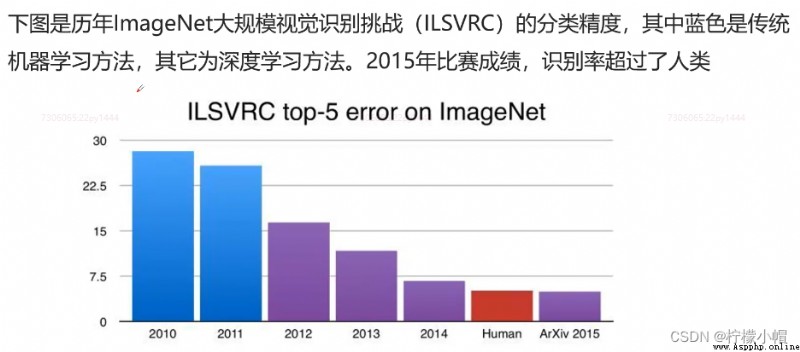
2.2 不需要特征工程
- 傳統機器學習需要人進行特征提取(特征工程),機器性能高度依賴於特征工程的質量。在特征很復雜的情況下,人就顯得無能為力。而深度學習不需要這樣的特征工程,只需將數據直接傳遞給深度學習網絡,由機器完成特征提取。
2.3 深度學習在大樣本數據下有更好的性能和擴展性
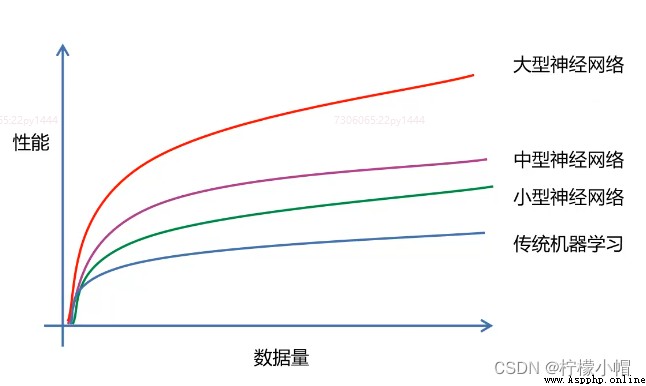
2.4 深度學習能解決傳統機器學習無法解決的問題(如深層次特征提取)
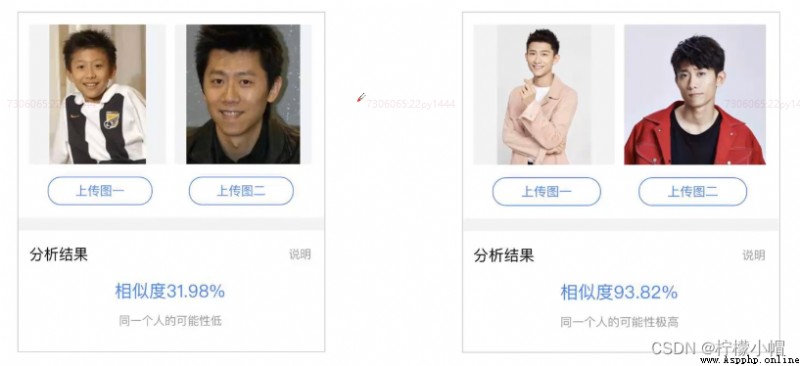
3. 深度學習的缺點
- 深度學習在小數據上性能不如傳統機器學習
- 深度學習網絡結構復雜、構建成本高
- 傳統機器學習比深度學習具有更好的解釋性
4. 深度學習與傳統機器學習對比
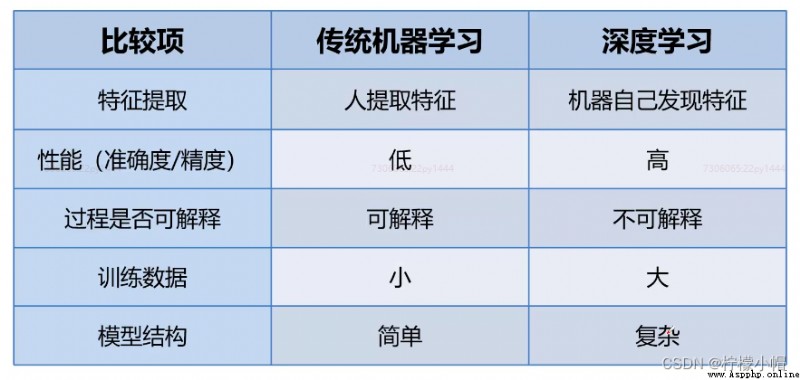
5. 為什麼要學習深度學習?
- 深度學習具有更強的解決問題能力(例如圖像識別准確率明顯超過機器學習,甚至超過了人類)
- 掌握深度學習具有更強的職業競爭力
- 深度學習在行業中應用更廣泛
四、深度學習的應用
- 圖像分類、人臉識別、圖像遷移、語音處理、自動駕駛、機器博弈、機器人、自然語言處理
五、深度學習總結
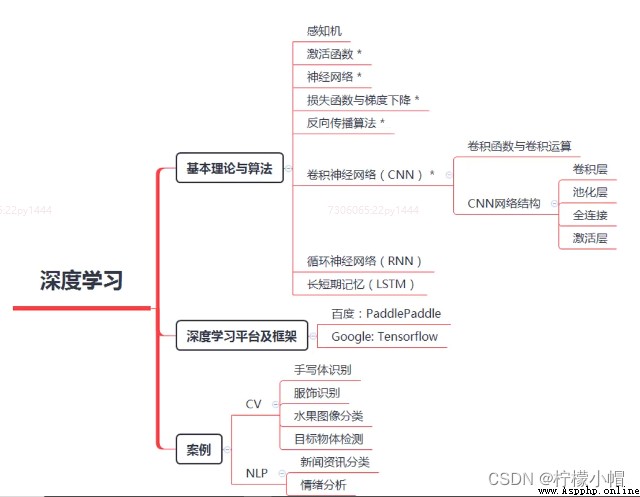
第二章 感知機與神經網絡
一、感知機概述
1. 什麼是感知機?
- 感知機(Perceptron),又稱神經元(Neuron)。是神經網絡(深度學習)的起源算法,1958年由康奈爾大學心理學教授弗蘭克·羅森布拉特(Frank Rosenblatt)提出,它可以接收多個輸入信號,產生一個輸出信號。
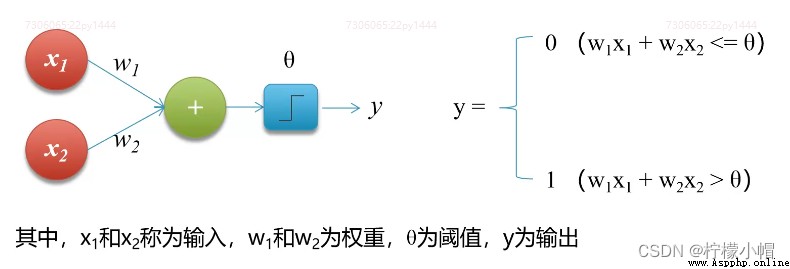
2. 感知機的功能
- 實現邏輯運算,包括邏輯和(AND)、邏輯或(OR)
- 實現自我學習
- 組成神經網絡
3. 實現邏輯和
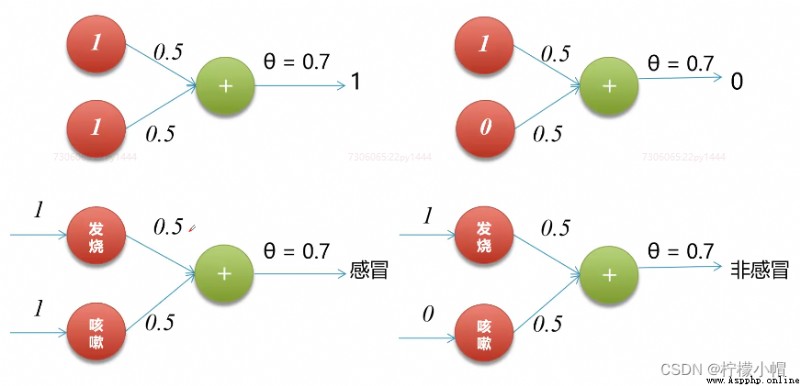
4. 實現邏輯或
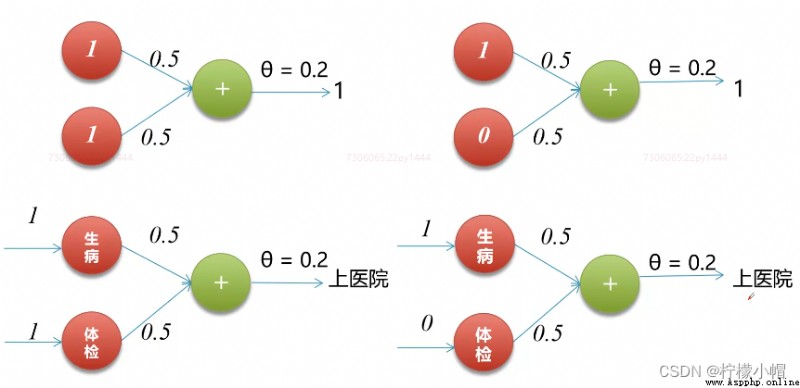
5. 感知機的缺陷
- 感知機的局限在於無法處理“異或”問題

6. 多層感知機
- 1975年,感知機的“異或”難題才被理論界徹底解決,即通過多個感知機組合來解決該問題,這種模型也叫多層感知機(Multi-Layer Perceptron,MLP)。如下圖所示,神經元節點阈值均設置為0.5
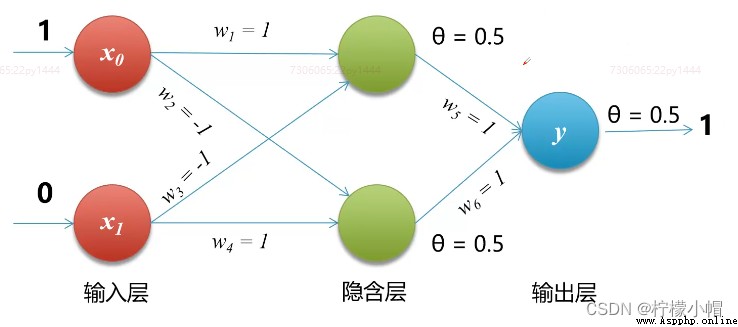
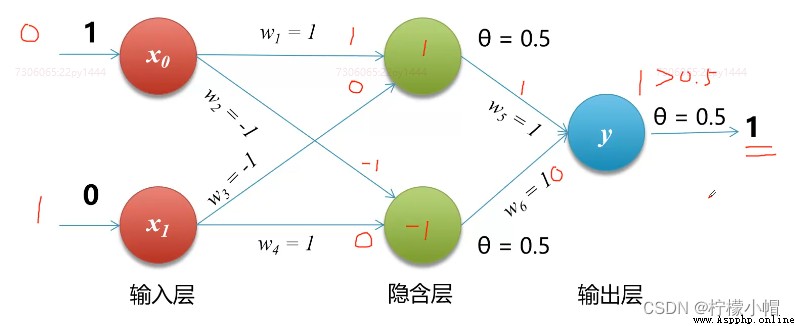
7. 代碼
# 自定義感知機
# 實現邏輯和
def AND(x1, x2):
w1, w2 = 0.5, 0.5 # 兩個權重
theta = 0.7 # 阈值
tmp = x1 * w1 + x2 * w2
if tmp <= theta:
return 0
else:
return 1
print(AND(1, 1)) # 1
print(AND(1, 0)) # 0
print(AND(0, 0)) # 0
# 實現邏輯或
def OR(x1, x2):
w1, w2 = 0.5, 0.5 # 兩個權重
theta = 0.2 # 阈值
tmp = x1 * w1 + x2 * w2
if tmp <= theta:
return 0
else:
return 1
print(OR(1, 1)) # 1
print(OR(1, 0)) # 1
print(OR(0, 0)) # 0
# 實現邏輯異或
def XOR(x1, x2):
s1 = not AND(x1, x2) # 對x1,x2做邏輯和計算,再取非
s2 = OR(x1, x2) # 直接對x1,x2做邏輯或計算
y = AND(s1, s2)
return y
print(XOR(1, 1)) # 0
print(XOR(1, 0)) # 1
print(XOR(0, 0)) # 0
二、神經網絡
1. 什麼是神經網絡?
- 感知機由於結構簡單,完成的功能十分有限。可以將若干個感知機連在一起,形成一個級聯網絡結構,這個結構稱為“多層前饋神經網絡”(Multi-layer Feedforward Neural Networks)。所謂“前饋”是指將前一層的輸出作為後一層的輸入邏輯結構。每一層神經元僅與下一層的神經元全連接。但在同一層之內,神經元彼此不連接,而且跨層之間的神經元,彼此也不相連。
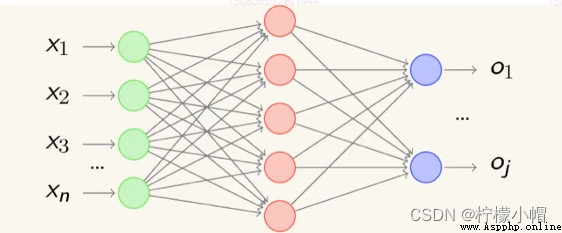
2. 神經網絡的功能
- 1989年,奧地利學者庫爾特·霍尼克(Kurt Hornik)等人發表論文證明,對於任意復雜度的連續波萊爾可測函數(Borel Measurable Function)f,僅僅需要一個隱含層,只要這個隱含層包括足夠多的神經元,前饋神經網絡使用擠壓函數(Spuashing Function)作為激活函數,就可以以任意精度來近似模擬f。如果想增加f的近似精度,單純依靠增加神經元的數目即可實現。
- 這個定理也被稱為通用近似定理(Universal Approximation Theorem),該定理表明,前饋神經網絡在理論上可近似解決任何問題。
3. 通用近似定理

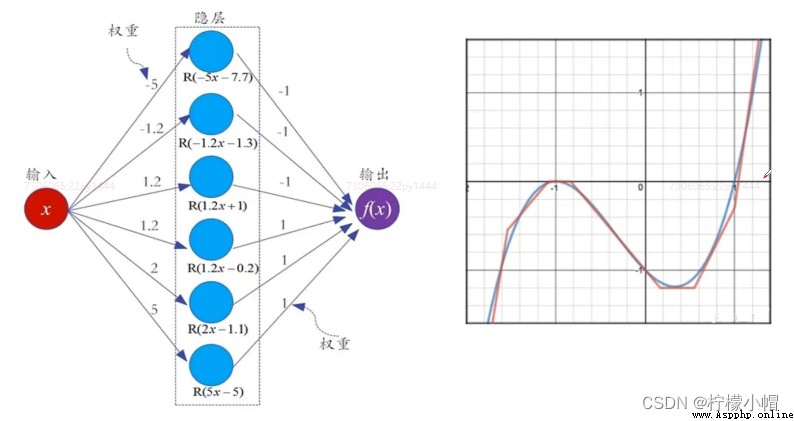
4. 深層網絡的優點
- 其實,神經網絡的結構還有另外一個“進化”方向,那就是朝著“縱深”方向發展,也就是說,減少單層的神經元數量,而增加神經網絡的層數,也就是“深”而“瘦”的網絡模型。
- 微軟研究院的科研人員就以上兩類網絡性能展開了實驗,實驗結果表明:增加網絡的層數會顯著提升神經網絡系統的學習性能。
三、激活函數
1. 什麼是激活函數?
- 在神經網絡中,將輸入信號的總和轉換為輸出信號的函數被稱為激活函數(activation function)
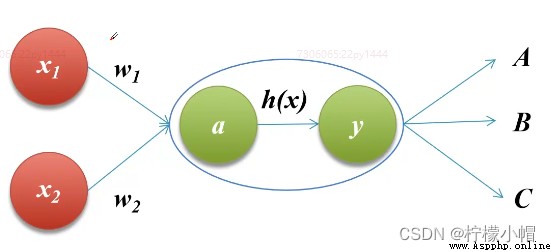
2. 為什麼使用激活函數?
- 激活函數將多層感知機輸出轉換為非線性,使得神經網絡可以任意逼近任何非線性函數,這樣神經網絡就可以應用到眾多的非線性模型中。
- 如果一個多層網絡,使用連續函數作為激活函數的多層網絡,稱之為“神經網絡”,否則稱為“多層感知機”。所以,激活函數是區別多層感知機和神經網絡的依據。
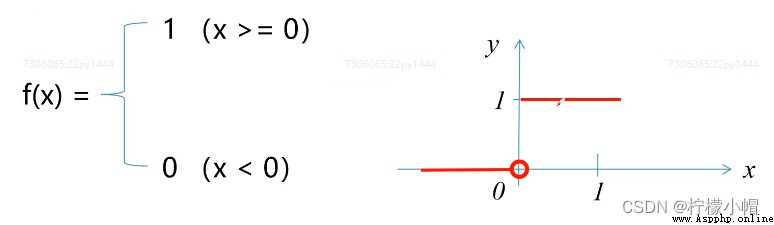
3. 常用激活函數 - 階躍函數
- 階躍函數(Step Function)是一種特殊的連續時間函數,是一個從0跳變到1的過程,函數形式與圖像:
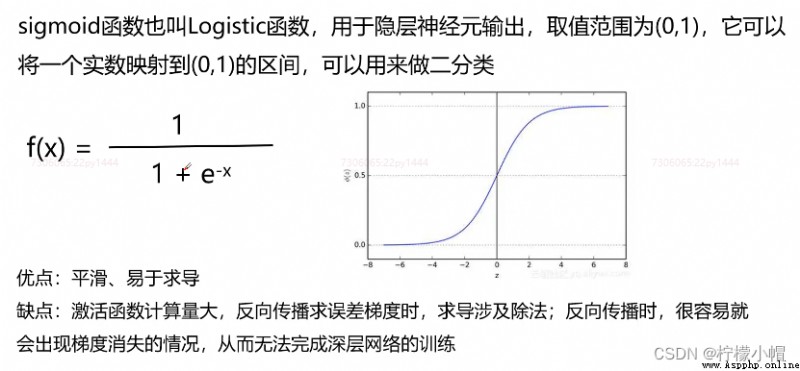
4. 常用激活函數 - sigmoid
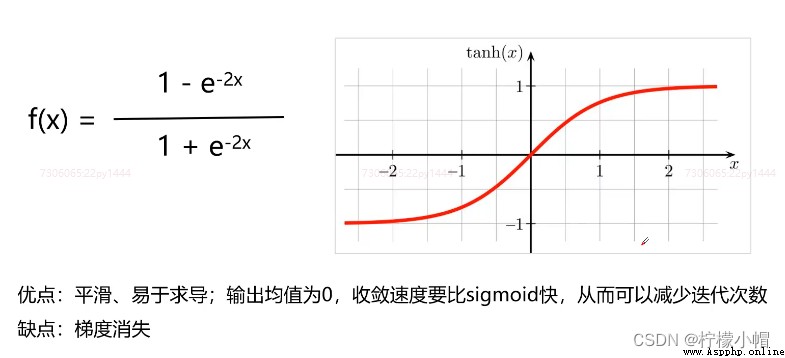
5. 常用激活函數 - tanh(雙曲正切)
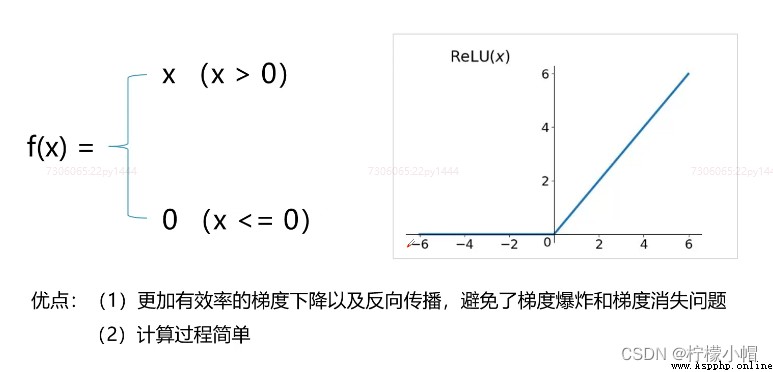
6. 常用激活函數 - ReLU(修正線性單元)
7. 常用激活函數 - Softmax

四、小結
- 多層前饋網絡。若干個感知機組合成若干層的網絡,上一層輸出作為下一層輸入。
- 激活函數。將計算結果轉換為輸出的值,包括階躍函數、sigmoid、tanh、ReLU






















