用 Taichi 加速 Python：提速 100+ 倍！

Python 已經成為世界上最流行的編程語言，尤其在深度學習、數據科學等領域占據主導地位。但是由於其解釋執行的屬性，Python 較低的性能很影響它在計算密集（比如多重 for 循環）的場景下發揮作用，實在讓人又愛又恨。如果你是一名經常需要使用 Python 進行密集計算的開發者，我相信你肯定會有下面的類似經歷：

• 我的 Python 程序裡面有個很大的 for 循環，循環體裡面全是密集的計算，跑起來好慢啊...

• 我的程序裡面只有一小部分計算是性能瓶頸，雖然可以用 C++ 改寫然後用 ctypes 綁定一下，但是那樣會很麻煩，還會有在別的機器上編譯不了的風險。我希望所有的工作都能在一個 Python 腳本中完成！

• 我之前是忠實的 C++/Fortran 用戶，但是最近周圍的同學用 Python 的越來越多，我也想試試 Python，但是無奈很多祖傳代碼用 Python 改寫以後就會慢 100 多倍，我接受不了...

• 我的工作中需要處理大量圖片數據，而需要的圖像處理功能 OpenCV 又不提供，只能自己手寫兩重 for 循環，在 Python 裡面這麼搞真是太痛苦了 ...

如果你有類似的煩惱，那真的值得了解一下 Taichi。我來簡單介紹一下：Taichi 是一個嵌入在 Python 中的領域特定語言，其一大功能就是加速 Python，讓 Python 代碼跑得和 C++ 甚至 CUDA 一樣快。Taichi 通過自己的編譯器將被 @ti.kernel 修飾的函數編譯到各種硬件上，包括 CPU 和 GPU，然後高性能執行。

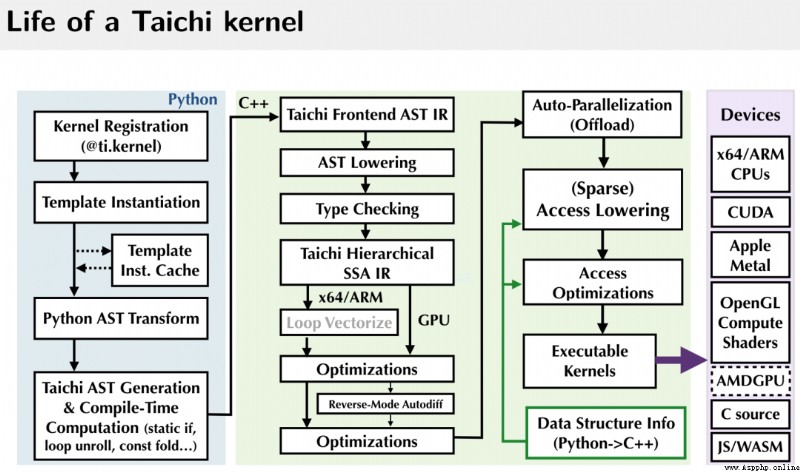
由於 Taichi 開發者社區花了大量的精力優化 Taichi 在 Python 中的使用體驗，所有的 Taichi 功能都可以在 import taichi as ti 以後使用，Taichi 本身也可以使用 pip 進行安裝。當然，Taichi 也可以與常用的 Python 包（numpy、matplotlib、PyTorch 等）進行交互。

在這篇文章中，我們將通過三個計算例子來演示如何使用 Taichi 讓你的 Python 輕松加速 > 50 倍。這三個例子是：1. 計算質數數目；2. 動態規劃求解最長公共子序列；3. 求解反應-擴散方程。

https://github.com/taichi-dev/faster-python-with-taichi

計算素數個數

作為開胃小菜，我們先做一個小實驗：計算小於給定正整數 的素數的個數。相信任何對 Python 有基礎了解的人都不難寫出類似下面這樣的解法：

"""Count the number of primes in range [1, n].
"""
def is_prime(n: int):
    result = True
    for k in range(2, int(n ** 0.5) + 1):
        if n % k == 0:
            result = False
            break
    return result
def count_primes(n: int) -> int:
    count = 0
    for k in range(2, n):
        if is_prime(k):
            count += 1
    return count
print(count_primes(1000000))

這個方法的思路簡單且粗暴：我們用一個函數 is_prime 來判斷某個正整數 是不是素數，是素數則返回 1，不是則返回 0。這只要遍歷檢查從 2 到 之間是否有整數能夠整除 即可。然後將小於 的全部整數依次代入此函數並統計結果。將上面的代碼保存為 count_primes.py，在命令行運行：

time python count_primes.py

在我的電腦上輸出的運行結果是：

78498
real        0m2.235s
user        0m2.235s
sys        0m0.000s

耗時 2.235 秒。也許代碼中 設置成一百萬對你的電腦來說太輕松了，要不要把 改成一千萬試試？我打賭不管你的電腦多麼高端，你起碼都要等個半分鐘才能看到結果。

好了下面是魔法時刻：我們不修改上面的函數體，只 import 一個“庫”，然後給兩個函數分別加一個裝飾器：

"""Count the number of primes below a given bound.
"""
import taichi as ti
ti.init()
@ti.func
def is_prime(n: int):
    result = True
    for k in range(2, int(n ** 0.5) + 1):
        if n % k == 0:
            result = False
            break
    return result
@ti.kernel
def count_primes(n: int) -> int:
    count = 0
    for k in range(2, n):
        if is_prime(k):
            count += 1
    return count
print(count_primes(1000000))

仍然運行 time python count_primes.py 命令，輸出的結果是：

78498
real        0m0.363s
user        0m0.546s
sys        0m0.179s

速度直接 x6! 而將 改成一千萬的話，Taichi 的耗時只會增加到 0.8s 左右，而 Python 則需要大約 55 秒，Taichi 直接加速了 70 倍！不僅如此，我們還可以在 ti.init 中加上 ti.init(arch=ti.gpu) 參數，指定 Taichi 使用 GPU 來進行計算。在 GPU 上同樣的計算 Taichi 只花了不到 0.45 秒，比 Python 足足快了 120 倍！你可以運行這裡的代碼親身體會一下。

上面這個計算素數的例子使用的方法有點土，作為習題還可以，但在實際生產中就顯得不那麼實用了。我們接下來看一個實際中普遍使用的算法。

動態規劃

動態規劃（Dynamic Programming）是一類特別實用的算法，這類算法的哲學是以空間換時間，通過存儲中間計算結果來減少重復計算量。我們這裡選擇一個求解最長公共子序列（Longest common subsequence, LCS）的例子 (算法導論的讀者有木有)。

插播兩個來自淵鳴的《算法導論》小故事：

1. 筆者小時候買過一本《算法導論》，書中提到四位作者都來自“麻雀理工學院”。當時還很好奇：怎麼會有學校叫這麼奇怪的名字... 過了一陣才意識到自己可能成了盜版書籍的受害者。

2. 10 年後，我還真的來到了麻省理工學院（MIT）讀博士，一年後進行碩士論文答辯（MIT 叫做 Research Qualification Exam），我自然就帶著 Taichi 的論文去了。答辯委員會裡面有一位慈祥的教授，Charles E. Leiserson，嗯，就是《算法導論》的作者之一，“CLRS” 之中的 L。

言歸正傳。所謂子序列，就是一個序列的子集，但是保持它們在原序列中的順序。比如說 [1, 2, 1] 是 [1, 2, 3, 1] 的子序列，而 [3, 2] 則不是。我們這裡考慮對兩條給定的序列，求出它們最長公共子序列的長度。最長公共子序列就是兩個序列的所有公共子序列中最長的一條 (這個最長子序列未必唯一，但它的長度是唯一確定的)。

舉個例子：

a = [0, 1, 0, 2, 4, 3, 1, 2, 1]

和

b = [4, 0, 1, 4, 5, 3, 1, 2]

的最長公共子序列是

LCS(a, b) = [0, 1, 4, 3, 1, 2]

最長公共子序列有很多應用。比如大家日常使用的 Linux diff 命令和 git 工具（比較兩個文件之間的相似度），還有生物信息學中判斷兩段基因的相似度（把數字換成 ACGT 就行），其中的實現都用到了 LCS。

動態規劃計算 LCS 的想法是我們依次求解序列 a 的前 i 個元素和序列 b 的前 j 個元素的最長公共子序列的長度，通過讓 i 和 j 逐漸增加我們就逐步得出了最終的結果。我們用 f[i, j] 表示 LCS((prefix(a, i), prefix(b, j)，其中 prefix(a, i) 表示序列 a 的前 i 個元素，即 a[0], a[1], ..., a[i - 1]。這樣我們就得到遞推式：

f[i, j] = max(f[i - 1, j - 1] + (a[i - 1] == b[j - 1]),
              max(f[i - 1, j], f[i, j - 1]))

於是，一個 LCS 算法用 Python 可以很自然地書寫為：

for i in range(1, len_a + 1):
    for j in range(1, len_b + 1):
        f[i, j] = max(f[i - 1, j - 1] + (a[i - 1] == b[j - 1]),
                      max(f[i - 1, j], f[i, j - 1]))

這裡我們給出一個 Taichi 的加速實現：

import taichi as ti
import numpy as np
ti.init(arch=ti.cpu)
benchmark = True
N = 15000
f = ti.field(dtype=ti.i32, shape=(N + 1, N + 1))
if benchmark:
    a_numpy = np.random.randint(0, 100, N, dtype=np.int32)
    b_numpy = np.random.randint(0, 100, N, dtype=np.int32)
else:
    a_numpy = np.array([0, 1, 0, 2, 4, 3, 1, 2, 1], dtype=np.int32)
    b_numpy = np.array([4, 0, 1, 4, 5, 3, 1, 2], dtype=np.int32)
@ti.kernel
def compute_lcs(a: ti.types.ndarray(), b: ti.types.ndarray()) -> ti.i32:
    len_a, len_b = a.shape[0], b.shape[0]
    ti.loop_config(serialize=True) # 避免 Taichi 自動並行
    for i in range(1, len_a + 1):
        for j in range(1, len_b + 1):
            f[i, j] = max(f[i - 1, j - 1] + (a[i - 1] == b[j - 1]),
                          max(f[i - 1, j], f[i, j - 1]))
    return f[len_a, len_b]
print(compute_lcs(a_numpy, b_numpy))

將上面的代碼保存為 lcs.py，然後在終端運行：

time python lcs.py

得到的結果為（具體結果每次未必一致）：

2721
real        0m1.409s
user        0m1.112s
sys        0m0.549s

我們在代碼中同時提供了分別使用 Taichi 和 Numpy 計算的版本，在我的電腦上對兩個長度是 N=15000 的隨機序列進行計算 Taichi 版本大約需要 0.9 秒，而 Python 則需要 476s，足足差了 500 多倍！大家可以運行一下體會 Taichi 相對 Numpy 那種飛一樣的感覺。

當然，Numpy 主要針對的場景是以數組為基本單位的運算，遇到這種需要在數組內更細粒度進行計算的情況就比較無力了。而這正是 Taichi 能夠發揮作用的地方。

反應 - 擴散方程

在大自然中我們常常會在動植物的表面見到一些有趣的圖案，比如斑馬身上的條紋，獵豹身上的斑點，河豚表面的花紋等等。

這些圖案看起來是不規則的，但是又有一定的規律，並不完全隨機。從進化的觀點，這些圖案是生物在長期演進和自然選擇中逐漸形成的，但到底是什麼規則決定了它們的形狀一直是個有趣的問題。阿蘭 . 圖靈 (正是圖靈機的發明人) 是最早注意到這一現象並嘗試給出模型描述的人。他在論文 "The Chemical Basis of Morphogenesis" 中提出可以用兩種化學物質 U, V 之間的相互作用來模擬圖案的形成過程，其中物質 U 的角色類似被捕食者 (prey)，物質 V 的角色類似捕食者 (predator)。它們之間的作用服從如下規則：

1. 初始時空間中隨機地分布了一些 U, V。

2. 在每個時刻 1, 2, 3, ..., U, V 兩種物質都向其鄰域擴散。

3. 當 U, V 相遇時，一定比例的 U, V 會合並轉化為更多的 V (捕食者在捕食後數量會增加)

4. 為了避免捕食者 V 的數量過多導致 U 的數量被消耗光，我們在每個時刻按照一定的比例 f 添加 U，同時按照一定的比例 k 移走 V。

於是整個過程可以用下面的反應 - 擴散方程描述：

這裡關鍵的控制參數有四個，分別是 ， 分別控制 U, V 的擴散速度， 代表 feed，控制 U 的添加量，而 代表 kill，控制移走 V 的比例。

為了在 Taichi 中模擬這一過程，我們將空間劃分為網格，每個網格中 U, V 的濃度值用一個 vec2 來表示。注意拉普拉斯算子 的數值計算是需要訪問當前網格周圍的網格的，為了避免一邊修改一邊讀取這種操作的發生，我們需要開辟兩個形狀為 的網格，每次用其中一個網格的值作為舊值，將更新後的濃度值寫入另一個網格中，然後交換兩個網格的角色。所以我們需要的數據結構應該是：

W, H = 800, 600
uv = ti.Vector.field(2, float, shape=(2, W, H))

初始時，我們假定網格中 U 的濃度處處是 1，然後隨機選擇 50 個點撒上 V：

import numpy as np
uv_grid = np.zeros((2, W, H, 2), dtype=np.float32)
uv_grid[0, :, :, 0] = 1.0
rand_rows = np.random.choice(range(W), 50)
rand_cols = np.random.choice(range(H), 50)
uv_grid[0, rand_rows, rand_cols, 1] = 1.0
uv.from_numpy(uv_grid)

實際的計算代碼非常之簡短：

@ti.kernel
def compute(phase: int):
    for i, j in ti.ndrange(W, H):
        cen = uv[phase, i, j]
        lapl = uv[phase, i + 1, j] + uv[phase, i, j + 1] + uv[phase, i - 1, j] + uv[phase, i, j - 1] - 4.0 * cen
        du = Du * lapl[0] - cen[0] * cen[1] * cen[1] + feed * (1 - cen[0])
        dv = Dv * lapl[1] + cen[0] * cen[1] * cen[1] - (feed + kill) * cen[1]
        val = cen + 0.5 * tm.vec2(du, dv)
        uv[1 - phase, i, j] = val

這裡我們使用了取值為 0 或 1 的整數 phase 來控制使用 uv 的哪一層來作為舊的網格，並將更新的值寫入 1-phase 對應的層中。

根據 V 的濃度進行染色，我們得到了如下的動畫效果:

非常有趣的是，雖然 V 的初始濃度是隨機設置的，但是最終得到的圖案卻具有相似性。

我們在代碼中提供了基於 Taichi 和 Numba 的兩份不同的實現，Taichi 的版本由於使用了 GPU 進行計算，計算的部分可以輕松達到 300+ fps，而 Numba 的版本計算部分雖然也是編譯執行的，但由於是在 CPU 上計算的，只有大約 30fps 左右。大家可以親自運行代碼體會一下 Taichi 使用 GPU 加速的巨大優勢。

總結

在這三個例子上 Taichi 都讓程序有了大幅加速。主要的性能來自三點：

1. Taichi 是編譯性的，而 Python 是解釋性的

2. Taichi 能自動並行，而 Python 通常是單線程的

3. Taichi 能在 GPU 上運行，而 Python 本身是在 CPU 上運行的

當然，加速 Python 還有很多其他工具，這裡我們分析一下他們和 Taichi 的優劣。

與 Numpy/JAX/PyTorch/TensorFlow 比較：這幾類工具都高度基於數組運算。計算的最小單位是數組，在 Data Science、Deep Learning 等領域是有明顯的優勢的。但是在科學計算領域，這樣做導致靈活性缺失：比如說前面那個計算質數的程序，就比較難使用數組運算表示出來。Taichi 的優勢就在於其靈活性，能夠直接操縱循環的每一次迭代，以一種更細顆粒度進行對於計算的描述，類似 C++ 和 CUDA。

與 Cython 比較：使用 Cython 編寫程序實現加速也是一種常見的選擇。在 Numpy 和 Scipy 的官方代碼中有不少模塊都是使用 Cython 編寫然後編譯的。但按照 Cython 的要求書寫代碼會比較麻煩，會犧牲一些可讀性。Cython 支持一定程度的並行計算，但不支持直接調用 GPU 進行計算。

與 Numba 比較：Numba 顧名思義，是非常適合針對 Numpy 進行加速的方案。當你的函數是針對 Numpy 的數組向量化的操作時，使用 Numba 將其編譯以後執行可以大大加速。Taichi 相比 Numba 的優勢還有：1. Taichi 支持各種靈活的數據類型，比如 struct, dataclass, quant, sparse 等等，你可以任意指定它們的內存排布，當數據量龐大時這個優勢會非常明顯。而 Numba 只有在針對 Numpy 的稠密數組時效果最佳。2. Taichi 可以調用不同的 GPU 後端進行計算，所以寫大規模並行程序（如粒子仿真、渲染器等）這種操作對 Taichi 來說是小菜一碟。但你很難想象可以用 Numba 寫一個還過得去的 (哪怕離線) 渲染器。

與 Pypy 比較：Pypy 是一個 Python 的 JIT 編譯器，這個工具 2007 年就有了，和 Taichi 的解決方案有些類似，都是通過編譯的方式加速 Python。Pypy 最大優勢在於 Python 代碼完全不用改變，就能通過 Pypy 加速。但是這也是 Pypy 加速比率比 Taichi 低的原因：因為 Pypy 需要在編譯的同時保持 Python 所有的語言特性，所以能夠進行的優化比較有限。而 Taichi 有一套自己的語法，雖然和 Python 很像但是也有自己的一些假設，這使得 Taichi 能夠實現更大的加速。

與 ctypes 比較：ctypes 可以讓用戶在 Python 中調用 C 函數。C++、CUDA 編寫的程序也可以用過 C 接口暴露給 Python 使用。但是，ctypes 會讓工具鏈復雜化：為了寫一段比較快的程序，用戶需要同時掌握 C、Python、CMake、CUDA 等等語言，和本文描述的完全在 Python 中解決問題的方案比起來還是麻煩了一些。

總而言之，在科學計算任務上，Taichi 還是有自己獨特的優勢的，大家可以根據自己的需求選擇最合適的工具。如果你需要在 Python 中實現類似 C/C++ 語言的性能，Taichi 不失為一個理想的選擇！

最後，我們希望 Taichi 能夠為你帶來價值，也希望能夠聽到你對 Taichi 的反饋，歡迎給我們提交 issues，加入 Taichi 開發者社區。如果想一鍵體驗 Taichi，只需要執行

pip install -U taichi

並執行

ti gallery

就可以體驗各種基於 Taichi 的高性能可視化 Demos，期待與大家相遇！

Python貓技術交流群開放啦！群裡既有國內一二線大廠在職員工，也有國內外高校在讀學生，既有十多年碼齡的編程老鳥，也有中小學剛剛入門的新人，學習氛圍良好！想入群的同學，請在公號內回復『交流群』，獲取貓哥的微信（謝絕廣告黨，非誠勿擾！）~

還不過瘾？試試它們

▲7 行代碼搞崩潰 B 站，原因令人唏噓！

▲收錢吧的 Python 高效自動化測試實踐

▲重寫 500 Lines or Less 項目：流水線調度問題

▲把Redis當作隊列來用，真的合適嗎？

▲14K 字，25 張圖徹底掌握分布式事務原理！

▲Python 的 heapq 模塊源碼分析

如果你覺得本文有幫助

請慷慨分享和點贊，感謝啦！