官方參考指南

OpenCV: Smoothing Images

一、模糊操作的原理

類似數學上的一維卷積操作，深度學習中的多維卷積運算。

二、均值濾波——blur()

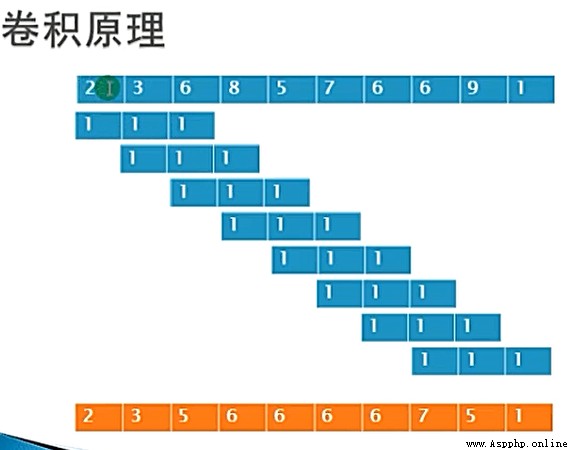
均值濾波用來模糊和平滑圖像，但是圖像失真比較大。

官方API文檔：OpenCV: Image Filtering-blur()

語法格式如下：

cv.blur(src, ksize[, dst[, anchor[, borderType]]]) ->dst 

• src是圖像數據，可以是任何通道的圖像，圖像的深度必須是CV_8U, CV_16U, CV_16S,  CV_32F or CV_64F中的一種
• ksize是卷積核的尺寸，不一定得是寬高相同，比如ksize=(1, 5)，也不一定是奇數比如ksize=(4, 4)
• anchor是卷積核的錨點，默認值是(-1, -1)，表示錨點是卷積核的中心
• borderType是邊界處理方式，詳見borderType官方文檔。

該API的卷積核的任何元素都是1，而卷積核權值就是元素個數的倒數，也即這是一個歸一化的卷積核。

因此，這個API名正言順地不愧為“均值濾波”的實現API之一。

二、方框濾波——boxFilter()

官方API文檔：OpenCV: Image Filtering-boxFilter()

語法格式如下：

cv.boxFilter(src, ddepth, ksize[, dst[, anchor[, normalize[, borderType]]]]) ->dst

• src是原圖像數據，雖然官方文檔沒做限制，但本人估計和blur()的條件一樣。
• ddepth是輸出圖像的位深度（不懂先轉向，位深決定色深），如果不設置就是取默認值-1，代表輸出圖像dst的位深度和原圖像src相同。其次還可以用其他位深度，詳見官方文檔Depth combinations。如下圖所示如果原圖是CV_8U，那麼輸出圖像可是CV_16S。但是也要注意如果前後位深度差別太大，可能會出現類似【iCCP: known incorrect sRGB profile】的錯誤，或者輸出圖像顯示上的問題，這個需要看ICCP是否支持。如果用OpenCV的位深度宏參數，需要在前面加模塊名，比如ddepth=cv.CV_16S。

• ksize是卷積核的尺寸，不一定得是寬高相同，比如ksize=(1, 5)，也不一定是奇數比如ksize=(4, 4)。
• anchor是卷積核的錨點，默認值是(-1, -1)，表示錨點是卷積核的中心。
• normalize是歸一化方式；默認是歸一化，此時方框濾波的卷積核外圍權值就為核元素求和的倒數，這時方框濾波等同於均值濾波blur()；如果不想要歸一化，需要設置normalize=False。
• borderType是邊界處理方式，如果不設置，默認是cv.BORDER_DEFAULT，詳見borderType官方文檔。

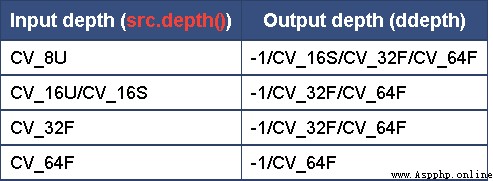
該API的卷積核的任何元素都是1，而卷積核權值默認是求和的倒數；只有normalize設置為False時才是一個非歸一化的卷積核。

三、中值濾波——medianBlur()

中值濾波一般用來去除椒鹽噪聲（salt-and-pepper noise），去噪效果顯著。

官方API文檔：OpenCV: Image Filtering-medianBlur()

語法格式如下。

cv.medianBlur(src, ksize[, dst]) ->dst

• src是原圖像變量，可以是單通道、三通道乃至四通道；位深度上，如果ksize是3或5，原圖像位深度就只能是CV_8U, CV_16U, or CV_32F，如果ksize更大，位深度就只能是CV_8U。
• ksize是濾波孔隙尺寸，必須是大於1的奇數，比如3\5\7\9；中值濾波不需要寫成長度為2的序列形式，也即ksize=3才是對的。

中值濾波最有意思的一點，就是不涉及到卷積運算，僅僅是比較運算得到孔隙內中值；所以沒有卷積核的概念，ksize是濾波孔隙尺寸。

四、高斯濾波——GaussianBlur()

高斯濾波相比均值濾波，不僅去噪效果好，而且圖像失真較少。

官方API文檔：OpenCV: Image Filtering-GaussianBlur()

高斯濾波的API-GaussianBlur()的語法如下。

cv.GaussianBlur(src, ksize, sigmaX[, dst[, sigmaY[, borderType]]]) ->dst

• src是圖像變量；通道數不限制，位深度必須是CV_8U, CV_16U, CV_16S, CV_32F or CV_64F其中之一。
• ksize是卷積核大小；卷積核的寬高可以不一樣，但是都必須是大於0的奇數，或者都等於0；如果都等於0 ，卷積核的大小由sigma計算。
• sigmaX代表X方向的高斯核標准差，本人猜測應該是寬度方向的分布標准差
• sigmaY代表Y方向的高斯核標准差，本人猜測應該是高度方向的分布標准差
• borderType是邊界處理方法，默認是cv.BORDER_DEFAULT，除了cv.BORDER_WRAP不支持，其他的方法詳見官檔。

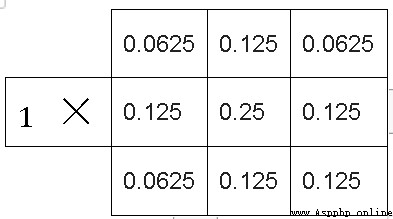
高斯濾波的卷積核不像均值濾波和方框濾波那樣元素全部相同，顧名思義——卷積核各元素共同組成高斯分布；如下圖所示，就屬於一個3*3的高斯核。

五、雙邊濾波——bilateralFilter()

雙邊濾波器可以有效去除噪聲，同時較好地保留邊緣銳度。但是，其速度比絕大多數濾波器都慢。

API中文參考文檔：opencv之bilateralFilter()函數_bilateralfilter函數

語法格式如下。

cv.bilateralFilter(src, d, sigmaColor, sigmaSpace[, dst[, borderType]]) ->dst

• src是原圖像數據，可以是單通道或三通道，可以是八位整型或浮點型。
• d是像素領域直徑，過大的濾波器會導致效率低（但是性能好）；對於實時應用，建議取d=5；對於需要過濾嚴重噪聲的離線應用，可取d=9；當d小於等於0時，自動由sigmaSpace的值確定（d與sigmaSpace成正比）。

sigma參數

• 簡單起見，可以將下面兩個sigma參數設置成同一值；如果他們很小（特別是小於10），就會導致雙邊濾波效果大打折扣，而如果他們很大（特別是大於150），就會導致濾波效果很好，但是也會使圖像看起來“卡通化”。
• sigmaColor是顏色空間的sigma參數，表示允許的色差范圍；換句話說，越大就會導致在像素領域內的色差越大的像素的顏色被混合，從而導致更大區域的半等色。
• sigmaSpace是坐標空間的sigma參數，表示允許的距離范圍；越大就會導致在sigmaColor色差范圍內的像素即使很遠也會被包括到。
• 一個d參數和兩個sigma參數結合起來，意思就是說在像素領域內、並且也在色差范圍和距離范圍之類的點就會被濾波處理。

• borderType是邊界處理方法，默認是cv.BORDER_DEFAULT，其他的方法詳見官檔。

雙邊濾波不支持原地處理圖像，也即不支持傳入src和dst同樣的變量。

六、圖像導數/梯度求解——sobel()和scharr()

6.1 Sobel()算子

參見Sobel算子的API文檔。​​​​​​​

sobel算子結合了高斯平滑和微分計算，主要用於邊緣檢測，其次還有去除噪點、平滑圖像。但是它檢測邊緣的位置精度不是很高。

語法格式如下。

cv.Sobel(src, ddepth, dx, dy[, dst[, ksize[, scale[, delta[, borderType]]]]]) ->dst

• src是原圖像。
• ddepth是輸出圖像位深度，同上述講解。
• dx、dy分別是x方向、y方向的微分次數；當dx=1、dy=0時表示求x方向的一階導數，當dx=0、dy=1時表示求y方向的一階導數（如果同時為1，通常得不到想要的結果）。
• ksize表示sobel算子的大小，必須是1、3、5或者7，默認為3；如果為-1（或者用宏參數，ksize=cv2.FILTER_SCHARR），表示采用更加精確的scharr算子。
• scale表示將梯度計算得到的數值放大的比例系數，效果通常使梯度圖更亮，默認為1。
• delta表示將目標圖像存儲進多維數組前，將每個像素值增加delta，默認為0。
• borderType表示邊界處理方式，同上述講解。

Sobel算子的3*3卷積核，見本文9.2小節。

為了避免負梯度時小於0被截斷為0（來自利用cv2.Sobel()計算圖像梯度的細節講解），最好將ddepth設置為CV_32F或CV_64F；sobel梯度計算完後，用一個convertScaleAbs將負像素點轉成正數並且深度轉成CV_8U，最後才用imshow()顯示；

或者，直接在讀取圖像後，對圖像對應的多維數組直接除以255，除完後數組的數據類型自動變為CV_64F，范圍在0-1之間，也即歸一化；在進行Sobel梯度運算（ddepth參數設置為-1即可）後再來一個取絕對值（不是用convertScaleAbs，而是用Python內置abs、Numpy中的abs或absolute），最後用imshow()顯示圖像，就可以規避問題；

前後兩種方法類似點在於都需在計算梯度前將圖像位深度轉成浮點型，避免負數梯度被截斷。

6.2 Scharr()算子

Scharr算子可以稱得上是對Sobel算子的優化；Scharr算子在處理邊緣時比Sobel精度高一些。

兩種算子的區別就是他們的卷積核不同；它們的計算耗時和算法復雜度相同。

官方API文檔：OpenCV: Image Filtering-Scharr()

語法格式如下

cv.Scharr(src, ddepth, dx, dy[, dst[, scale[, delta[, borderType]]]]) ->dst

• src是原圖像，同Sobel。
• ddepth是圖像位深度，同Sobel。
• dx和dy分別是寬度方向梯度導數階數、高度方向梯度導數階數，同Sobel。
• scale是比例系數，同Sobel。
• delta是偏差系數，同Sobel。
• borderType是邊界處理類型，同Sobel。

可以看出！

cv.Scharr(src, ddepth, dx, dy[, dst[, scale[, delta[, borderType]]]])

和

cv.Sobel(src, ddepth, dx, dy[, dst[, ksize=cv2.FILTER_SCHARR[, scale[, delta[, borderType]]]]]) ->dst

完全相同！

七、自定義圖像分離濾波——filter2D()

官方API文檔：OpenCV: Image Filtering-filter2D()

語法如下：

cv.filter2D(src, ddepth, kernel[, dst[, anchor[, delta[, borderType]]]]) ->dst

• src是待處理圖像，不限制通道數和位深度；支持原地操作圖像，也即支持傳入src和dst同樣的變量。
• ddepth是輸出圖像的位深度，默認是-1，和原圖相同。其他信息詳見本文第二部分方框濾波API的參數ddepth的講解。
• kernel是卷積核或者相關區域孔隙；只能是單通道浮點矩陣，因此如果你想要給多通道圖像的不同通道以不同的核進行運算，你可以先用split()將通道分離，然後分別傳入不同核的filter2D()進行運算。如果Kernel很小，函數使用的是直接簡單的算法，而如果kernel是11*11或更大，就是用復雜的DFT算法。kernel是需要程序員手動傳入的，可以是逐個元素一一開列的ndarray，也可是用np.ones()定義出來的全為1的矩陣，也可是用一些生成卷積核的API，比如getStructuringElement、getGaussianKernel。
• anchor用來表示卷積核錨點相對於卷積核的坐標，默認是(-1, -1)，表示錨點位於卷積核的中心。
• delta是圖像偏移值，默認為0，也即不偏移；含義，卷積運算或相關運算後再給每個像素點加上一個delta偏移值；也即dst=src × kernel + delta。
• borderType是邊界處理方法，默認是cv.BORDER_DEFAULT，其他的方法詳見官檔。

八、自定義圖像濾波——sepFilter2D()

第三方參考資料：OpenCV每日函數 圖像過濾模塊 (20) sepFilter2D函數

可分離濾波的API官方文檔：OpenCV: Image Filtering-sepFilter2D()

語法格式如下：

cv.sepFilter2D(src, ddepth, kernelX, kernelY[, dst[, anchor[, delta[, borderType]]]]) ->dst

• src是原圖像。
• ddepth是輸出圖像dst的位深度；具體規則詳見本文第二部分方框濾波API的參數ddepth的講解。
• kernelX是橫向單維卷積核，需要人為傳入具體到每個元素取值的卷積核；比如kernelX=np.array[-1, 3, -1]。
• kernelY是縱向單維卷積核，需要人為傳入具體到每個元素取值的卷積核；；比如kernelY=np.array[-1, 3, -1]。
• dst是輸出圖像，寬高和通道數與原圖相同。
• anchor是卷積核錨點，與上同。
• delta是偏差值，卷積後全部元素與此值相加。
• borderType是邊界處理方式，與上同；cv.BORDER_WRAP不支持。

可分離濾波器算法的運算機制：先用kernelX進行卷積運算，然後再將第一次卷積運算的結果用kernelY進行卷積，最後每個元素加上delta偏差值。

可分離濾波器算法的優點：假設圖像面積為A，按照filter2D()來卷積，卷積核是K*K大小，那麼最後運算量與A*K*K成正比；而如果同一圖像按照sepFilter2D()來卷積，橫、縱卷積核長度都是K，最後運算量與2*A*K成正比；當K大於等於3時（普遍情況正如此），明顯前者運算量更大；因此可分離濾波器的運算速度很快！

九、不同應用場景下的卷積核（Convolutional Kernel）

9.1 模糊/平滑

（1）均值濾波的卷積核

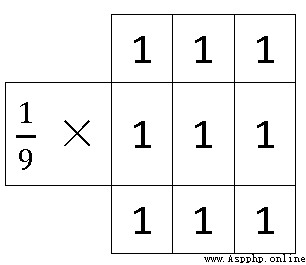
（2）高斯模糊的卷積核

9.2 梯度

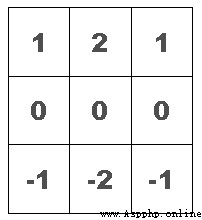
（1）垂直梯度-bottom sobel

（2）垂直梯度-top sobel

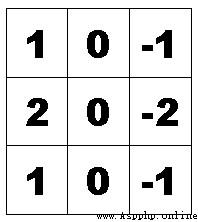
（3）水平梯度-left sobel

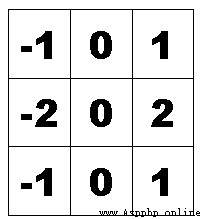
（4）水平梯度-right sobel

9.3 浮雕（Emboss）

浮雕本質就是在給定方向上的梯度，比如下面這個kernel是135°上的梯度。

9.4 輪廓（Outline）

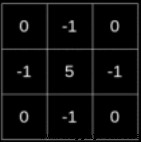
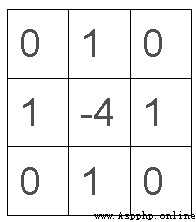
如果想要檢測輪廓，可以用下面的核；中間是8，鄰近的所有像素點都是-1；表示如果中間像素與周圍像素點的值相近，最後得到的取值很小，偏向於黑色。

9.5 銳化（Sharpen）

銳化是指加大相鄰像素點之間的色差；下圖即是一個銳化卷積核，假設中央是x，而-1的位置對應y，那麼最後得到的取值是5x-4y；與相鄰像素點的差值由原來的x-y變成了5(x-y)，顯然差的絕對值更大了。

9.6 拉普拉斯算子（Laplacian Operator）

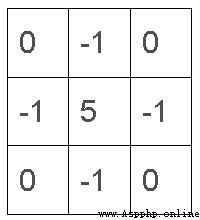
一般用來檢測邊緣，當然也可用來檢測圖像中的模糊。

9.7 分身（Identity）

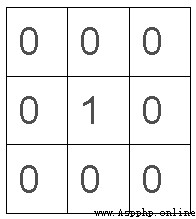
當卷積核的錨點元素為1，而其他元素都為0時，代表卷積得到的結果圖與原圖別無二致。

十、生成卷積核（Convolutional Kernel）或相關區域孔隙（Correlation Aperture）的方法

10.1 結構元素——getStructuringElement()

不僅可以用來生成卷積核，也可用來生成供腐蝕（erode或morphologyEx + cv.MORPH_ERODE）、膨脹（dilate或morphologyEx + cv.MORPH_DILATE）、開運算（morphologyEx + cv.MORPH_OPEN）、閉運算（morphologyEx + cv.MORPH_CLOSE）、形態學梯度（morphologyEx + cv.MORPH_GRADIENT）、頂帽運算（morphologyEx + cv.MORPH_TOPHAT）、黑帽運算（morphologyEx + cv.MORPH_BLACKHAT）所需的結構元素。

cv.getStructuringElement(shape, ksize[, anchor]) ->retval

• shape是結構元素的形狀，一共可以有矩形（寬高可不同）、橢圓、交叉十字三種；分別對應的OpenCV宏參數是cv.MORPH_RECT、cv.MORPH_ELLIPSE、cv.MORPH_CROSS。
• ksize是結構元素的最小外切矩形（也稱結構元素的矩形背景）寬高；如果結構元素本身就是矩形，也就是結構元素的寬高；如果結構元素是橢圓或交叉十字，那麼是橢圓或交叉十字形狀的最小外切矩形的寬高。
• anchor是結構元素的中心點，默認值是(-1, -1)，處於正中央；傳入anchor的坐標顯然應該是相對於結構元素的相對坐標；如果形狀是矩形，不管傳入什麼anchor最後結果都是全1矩形；如果形狀是橢圓，anchor指橢圓中心點相對於結構元素矩形背景的相對坐標。 
• retval就是結構元素了。

下面給代碼例程，輔助大家對該API的理解；我們可以看到所有的點取值都是1，只不過形狀構成不同罷了！

import cv2 as cv
def filter_custom():
rect_ker = cv.getStructuringElement(cv.MORPH_RECT, (7, 7))
elli_ker = cv.getStructuringElement(cv.MORPH_ELLIPSE, (7, 7))
cross_ker = cv.getStructuringElement(cv.MORPH_CROSS, (7, 7))
print(rect_ker.dtype)
print(elli_ker.dtype)
print(cross_ker.dtype)
print(rect_ker)
print(elli_ker)
print(cross_ker)
filter_custom()
cv.waitKey(0)
cv.destroyAllWindows()

輸出如下。

uint8
uint8
uint8
[[1 1 1 1 1 1 1]
[1 1 1 1 1 1 1]
[1 1 1 1 1 1 1]
[1 1 1 1 1 1 1]
[1 1 1 1 1 1 1]
[1 1 1 1 1 1 1]
[1 1 1 1 1 1 1]]
[[0 0 0 1 0 0 0]
[0 1 1 1 1 1 0]
[1 1 1 1 1 1 1]
[1 1 1 1 1 1 1]
[1 1 1 1 1 1 1]
[0 1 1 1 1 1 0]
[0 0 0 1 0 0 0]]
[[0 0 0 1 0 0 0]
[0 0 0 1 0 0 0]
[0 0 0 1 0 0 0]
[1 1 1 1 1 1 1]
[0 0 0 1 0 0 0]
[0 0 0 1 0 0 0]
[0 0 0 1 0 0 0]]

10.2 高斯卷積核——getGaussianKernel()

​​​​​​​語法格式如下。

cv.getGaussianKernel(ksize, sigma[, ktype]) ->retval

• ksize是高斯卷積核的長度，需要是大於0的奇數。
• sigma是高斯函數的標准差σ參數，越大數值越分散。如果sigma取值小於等於0，就由ksize的大小推算，公式為sigma = 0.3*((ksize-1)*0.5 - 1) + 0.8。
• ktype是高斯卷積核的數據類型，可以是CV_32F或CV_64F。

這個生成高斯核的方式，和GaussianBlur()生成的卷積核不同，這種方法得到的卷積核只能是ksize * 1的形狀。

但是，這兩種方式得到的卷積核的權重值求和都是1，因為如果不為1，往往是錯誤的。

10.3 導數卷積核——getDerivKernels() 

該函數可以用來生成用於計算圖像導數的濾波器系數，

語法格式如下。

cv.getDerivKernels(dx, dy, ksize[, kx[, ky[, normalize[, ktype]]]]) ->kx, ky

• dx和dy表示x、y軸方向上的導數階數；同Sobel
• ksize表示生成的兩個一維卷積核的長度，因此ksize只用傳一個整數即可；ksize可以是-1（FILTER_SCHARR）、1、3、5、7。如果ksize設置成-1或FILTER_SCHARR，那麼kx和ky從scharr算子上的第一列、第一行拆分；反之，從sobel算子上的第一列、第一行拆分。
• normalize表示是否歸一化標志，默認取值是False，也即不歸一化。如果設置為True，那麼所有權值都要除以2^(ksize∗2−dx−dy−2)。一般來說，如果用來濾波的圖像的位深度是浮點型，那麼就需要歸一化；如果用來濾波的圖像是8位無符號整型，就需要將結果存儲在 16 位圖像中，以保留所有小數位，不用歸一化。
• ktype是卷積核的數據類型，可以是CV_32F（默認）或CV_64F。
• kx和ky分別表示x、y軸方向上的從sobel算子、scharr算子上第一列、第一行拆分的一維卷積核。返回的結果，可以傳入sepFilter2D()；或者傳遞給createSeparableLinearFilter()創建線性可分的過濾器。

比如說因為3*3的sobel算子的如下

取出第一列作為dx，那麼dx=[[-1], [0], [1]]；取出第一行作為dy，也即dy=[[-1], [2], [-1]]。

10.4 特征卷積核——getGaborKernel 

這個卷積核，一般用來提取特征；特別是人臉特征識別，經常用到該函數。

該函數由兩部分組成——高斯函數（對應標准差參數sigma和均值參數theta）和正余弦函數，

參考自Gabor濾波簡介與Opencv中的實現及參數變化實驗

語法格式如下。

cv.getGaborKernel(ksize, sigma, theta, lambd, gamma[, psi[, ktype]]) ->retval

• ksize是卷積核的大小。
• sigma是高斯核函數的標准查，希臘字母是σ。
• theta是高斯核函數的均值，希臘字母是θ。
• lambd是正余弦函數波長，希臘字母是λ。
• gamma是長寬比，決定這Gabor核函數圖像的橢圓率，希臘字母是γ。
• psi是正余弦函數的相位偏移量，取值范圍是-180~180，希臘字母是ψ。
• ktype是卷積核的數據類型，可以是CV_32F（默認）或CV_64F。
• retval是輸出的卷積核。