時間序列(Time Series)是一組按照時間發生先後順序進行排列的數據點序列。通常一組時間序列的時間間隔為定值間隔(如1秒,1分鐘,1天,1個月,1年等),因此時間序列可以作為離散時間數據進行分析處理。時間序列廣泛應用於數理統計、信號處理、計量經濟學、天氣預報、地震預測、腦電圖、控制工程、航空學、通信工程以及絕大多數涉及到時間數據測量的應用科學與工程學。
股票價格走勢: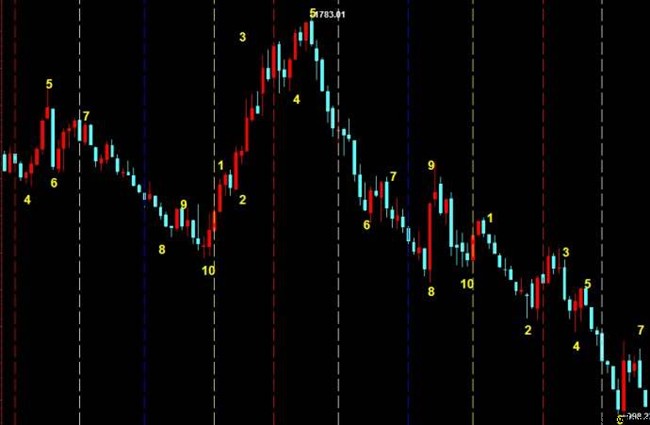
地震強度時序圖: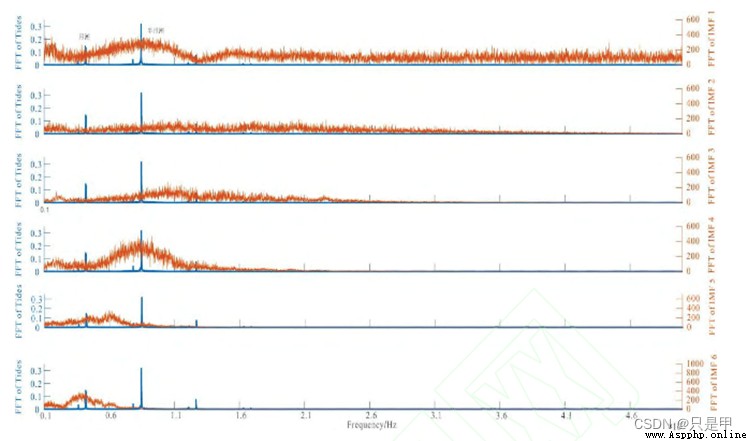
平穩性就是要求經由樣本時間序列所得到的擬合曲線
在未來的一段期間內仍能順著現有的形態“慣性”地延續下去
平穩性要求序列的均值和方差不發生明顯變化
嚴平穩:
嚴平穩表示的分布不隨時間的改變而改變。
如:白噪聲(正態),無論怎麼取,都是期望為0,方差為1
弱平穩:
期望與相關系數(依賴性)不變
未來某時刻的t的值Xt就要依賴於它的過去信息,所以需要依賴性
ARIMA 中的 I 就是差分法
差分法:時間序列在t與t-1時刻的差值
原數據: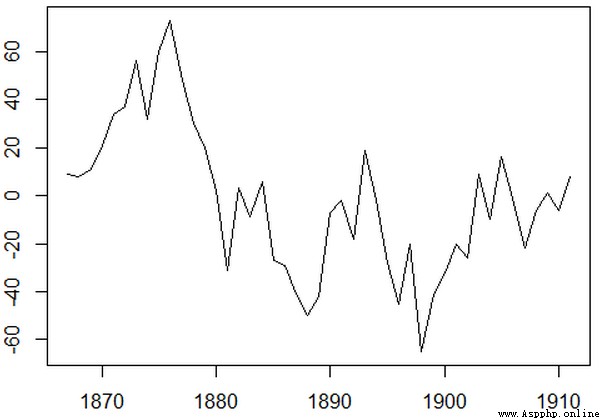
一階差分:
原始數據的波動太大,如果我們換成一階差分,數據看起來就會平穩很多,如果一階差分波動依舊大,我們可以轉換為多階差分。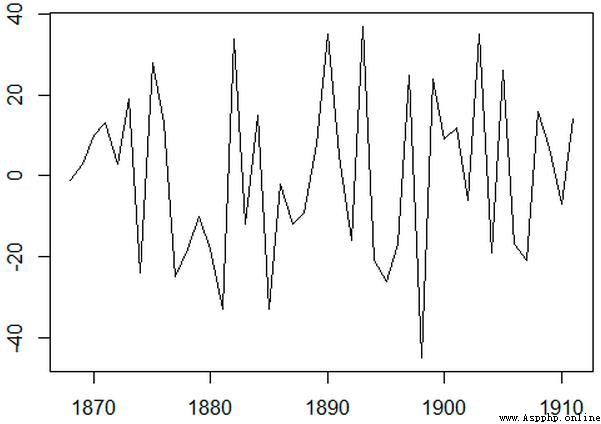
描述當前值與歷史值之間的關系,用變量自身的歷史時間數據對自身進行預測
自回歸模型必須滿足平穩性的要求
p階自回歸過程的公式定義: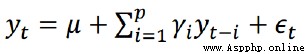

自回歸模型的限制:
移動平均模型關注的是自回歸模型中的誤差項的累加
q階自回歸過程的公式定義: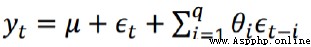
移動平均法能有效地消除預測中的隨機波動
ARMA 自回歸與移動平均的結合
公式定義: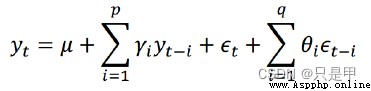
ARIMA(p,d,q)模型全稱為差分自回歸移動平均模型
(Autoregressive Integrated Moving Average Model,簡記ARIMA)
AR是自回歸,p為自回歸項;
MA為移動平均,q為移動平均項數,d為時間序列成為平穩時所做的差分次數
原理:
將非平穩時間序列轉化為平穩時間序列然後將因變量僅對它的滯後值以及隨機誤差項的現值和滯後值進行回歸所建立的模型
有序的隨機變量序列與其自身相比較
自相關函數反映了同一序列在不同時序的取值之間的相關性
公式:
Pk的取值范圍為[-1,1]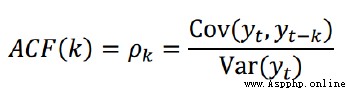
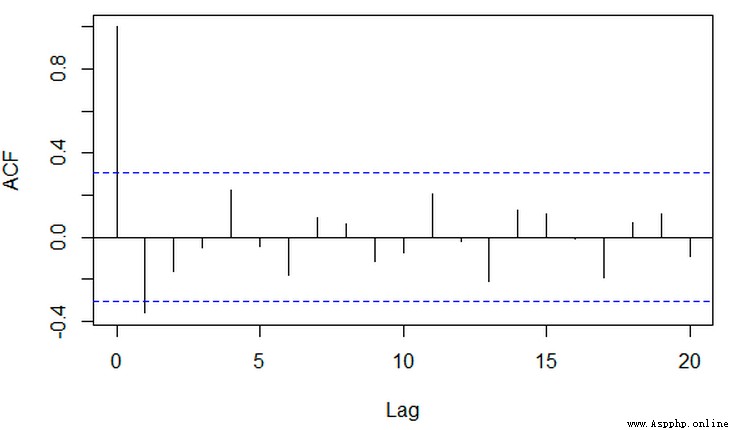
對於一個平穩AR§模型,求出滯後k自相關系數p(k)時
實際上得到並不是x(t)與x(t-k)之間單純的相關關系
x(t)同時還會受到中間k-1個隨機變量x(t-1)、x(t-2)、……、x(t-k+1)的影響
而這k-1個隨機變量又都和x(t-k)具有相關關系
所以自相關系數p(k)裡實際摻雜了其他變量對x(t)與x(t-k)的影響
剔除了中間k-1個隨機變量x(t-1)、x(t-2)、……、x(t-k+1)的干擾之後
x(t-k)對x(t)影響的相關程度。
ACF還包含了其他變量的影響
而偏自相關系數PACF是嚴格這兩個變量之間的相關性
截尾:落在置信區間內(95%的點都符合該規則)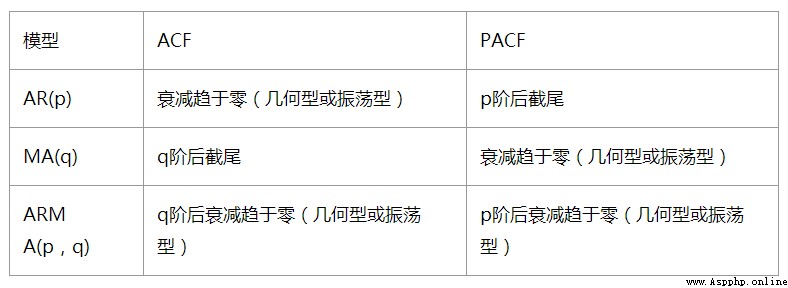
AR§ 看PACF
MA(q) 看ACF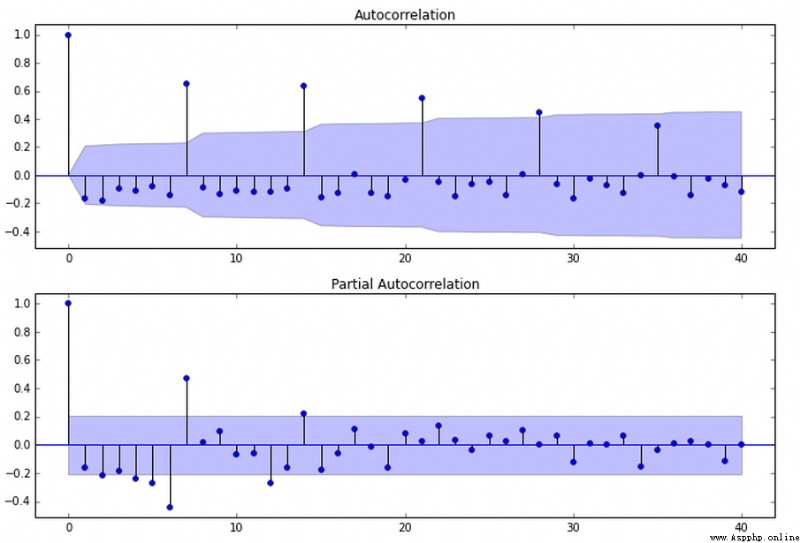
將序列平穩(差分法確定d)
p和q階數確定:ACF與PACF
ARIMA(p,d,q)
模型選擇AIC與BIC: 選擇更簡單的模型
AIC:赤池信息准則(AkaikeInformation Criterion,AIC)
𝐴𝐼𝐶=2𝑘−2ln(𝐿)
BIC:貝葉斯信息准則(Bayesian Information Criterion,BIC)
𝐵𝐼𝐶=𝑘𝑙𝑛𝑛−2ln(𝐿)
k為模型參數個數,n為樣本數量,L為似然函數
ARIMA模型的殘差是否是平均值為0且方差為常數的正態分布
QQ圖:線性即正態分布