機器學習強基計劃聚焦深度和廣度,加深對機器學習模型的理解與應用。“深”在詳細推導算法模型背後的數學原理;“廣”在分析多個機器學習模型:決策樹、支持向量機、貝葉斯與馬爾科夫決策、強化學習等。
詳情:機器學習強基計劃
本期目標:實現這樣一個效果
線性模型的假設形式是屬性權重、偏置與屬性的線性組合,即
f ( x ( i ) ) = w T x ( i ) + b f\left( \boldsymbol{x}^{\left( i \right)} \right) =\boldsymbol{w}^T\boldsymbol{x}^{\left( i \right)}+b f(x(i))=wTx(i)+b
其中 x ( i ) = [ x 1 ( i ) x 2 ( i ) ⋯ x d ( i ) ] T \boldsymbol{x}^{\left( i \right)}=\left[ \begin{matrix} x_{1}^{\left( i \right)}& x_{2}^{\left( i \right)}& \cdots& x_{d}^{\left( i \right)}\\\end{matrix} \right] ^T x(i)=[x1(i)x2(i)⋯xd(i)]T是數據集 D D D中的第 i i i個樣本, x j ( i ) ( j = 1 , 2 , ⋯ , d ) x_{j}^{\left( i \right)}\left( j=1, 2, \cdots , d \right) xj(i)(j=1,2,⋯,d)是該數據集樣本的 d d d個屬性; w = [ w 1 w 2 ⋯ w d ] T \boldsymbol{w}=\left[ \begin{matrix} \boldsymbol{w}_1& \boldsymbol{w}_2& \cdots& \boldsymbol{w}_d\\\end{matrix} \right] ^T w=[w1w2⋯wd]T是樣本屬性的權重向量; b b b是模型偏置。
上式也可寫為齊次形式
f ( x ( i ) ) = w ^ T [ x ( i ) 1 ] f\left( \boldsymbol{x}^{\left( i \right)} \right) =\boldsymbol{\hat{w}}^T\left[ \begin{array}{c} \boldsymbol{x}^{\left( i \right)}\\ 1\\\end{array} \right] f(x(i))=w^T[x(i)1]
其中系數向量 w ^ = [ w ; b ] \boldsymbol{\hat{w}}=\left[ \boldsymbol{w}; b \right] w^=[w;b]
進一步,考慮單調可微函數 g ( ⋅ ) g\left( \cdot \right) g(⋅),令
f ( x ( i ) ) = g − 1 ( w T x ( i ) + b ) f\left( \boldsymbol{x}^{\left( i \right)} \right) =g^{-1}\left( \boldsymbol{w}^T\boldsymbol{x}^{\left( i \right)}+b \right) f(x(i))=g−1(wTx(i)+b)
稱為廣義線性模型(generalized linear model),其中 g ( ⋅ ) g\left( \cdot \right) g(⋅)稱為聯系函數(link function)。
廣義線性模型本質上仍是線性的,但通過 g ( ⋅ ) g\left( \cdot \right) g(⋅)進行非線性映射,使之具有更強的擬合能力,類似神經元的激活函數。例如對數線性回歸(log-linear regression)是 g ( ⋅ ) = ln ( ⋅ ) g\left( \cdot \right) =\ln \left( \cdot \right) g(⋅)=ln(⋅)時的情形,此時模型擁有了指數逼近的性質。
線性模型的優點是形式簡單、易於建模、可解釋性強,是更復雜非線性模型的基礎。
感知機(Perceptron)是最簡單的二分類線性模型,也是神經網絡的起源算法,如圖所示。
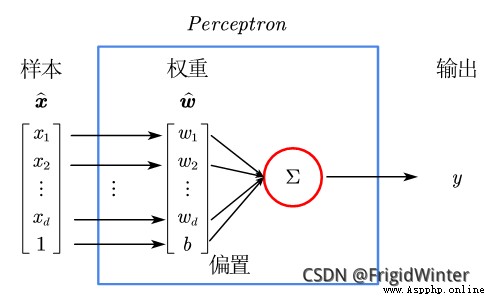
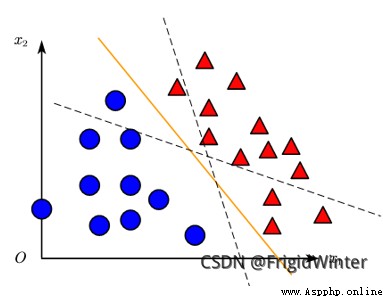
y = w ^ T x ^ y=\boldsymbol{\hat{w}}^{\boldsymbol{T}}\boldsymbol{\hat{x}} y=w^Tx^是 R d \mathbb{R} ^d Rd空間的一條直線,因此感知機實質上是通過訓練參數 w ^ \boldsymbol{\hat{w}} w^改變直線位置,直至將訓練集分類完全,如圖所示,或者參考文章開頭的動圖。
機器學習強基計劃的初衷就是搞清楚每個算法、每個模型的數學原理,讓我們開始吧!
感知機的損失函數定義為全體誤分類點到感知機切割超平面的距離之和:
E ( w ^ ) = 1 ∥ w ^ ∥ ∑ i = 1 n ∣ w ^ T x ^ e r r o r ( i ) ∣ E\left( \boldsymbol{\hat{w}} \right) =\frac{1}{\left\| \boldsymbol{\hat{w}} \right\|}\sum_{i=1}^n{\left| \boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}_{error}^{\left( i \right)} \right|} E(w^)=∥w^∥1i=1∑n∣∣w^Tx^error(i)∣∣
對於二分類問題 y ∈ { − 1 , 1 } y\in \left\{ -1, 1 \right\} y∈{ −1,1},則誤分類點的判斷方法為 − y i w ^ T x ^ e r r o r ( i ) > 0 -y_i\boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}_{error}^{\left( i \right)}>0 −yiw^Tx^error(i)>0
- 假如 y i = − 1 y_i=-1 yi=−1為反例,但是誤判為正例(樣本點在直線上方),則 w ^ T x ^ e r r o r ( i ) > 0 \boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}_{error}^{\left( i \right)}>0 w^Tx^error(i)>0,所以 − y i w ^ T x ^ e r r o r ( i ) > 0 -y_i\boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}_{error}^{\left( i \right)}>0 −yiw^Tx^error(i)>0
- 假如 y i = 1 y_i=1 yi=1為正例,但是誤判為反例(樣本點在直線下方),則 w ^ T x ^ e r r o r ( i ) < 0 \boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}_{error}^{\left( i \right)}<0 w^Tx^error(i)<0,所以 − y i w ^ T x ^ e r r o r ( i ) > 0 -y_i\boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}_{error}^{\left( i \right)}>0 −yiw^Tx^error(i)>0
這在二分類問題中是個很常用的技巧,後面還會遇到這種等效形式。
從而損失函數也可簡化為下面的形式以便於求導:
E ( w ^ ) = − ∑ i = 1 n y i w ^ T x ^ e r r o r ( i ) E\left( \boldsymbol{\hat{w}} \right) =-\sum_{i=1}^n{y_i\boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}_{error}^{\left( i \right)}} E(w^)=−i=1∑nyiw^Tx^error(i)
這裡省略了 1 ∥ w ^ ∥ \frac{1}{\left\| \boldsymbol{\hat{w}} \right\|} ∥w^∥1是因為直線
w ^ T x ^ = 0 \boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}=0 w^Tx^=0
方程兩邊同時乘以系數都成立,所以直線系數 w ^ \boldsymbol{\hat{w}} w^可以隨意縮放,這裡可令 ∥ w ^ ∥ = 1 \left\| \boldsymbol{\hat{w}} \right\|=1 ∥w^∥=1
若采用梯度下降法進行優化(梯度法可參考圖文詳解神秘的梯度下降算法原理(附Python代碼)),則算法流程為:
class Perceptron:
def __init__(self):
self.w = np.mat([0,0]) # 初始化權重
self.b = 0 # 初始化偏置
self.delta = 1 # 設置學習率為1
self.train_set = [[np.mat([3, 3]), 1], [np.mat([4, 3]), 1], [np.mat([1, 1]), -1]] # 設置訓練集
self.history = [] # 訓練歷史
def update(self,error_point):
self.w += self.delta*error_point[1]*error_point[0]
self.b += self.delta*error_point[1]
self.history.append([self.w.tolist()[0],self.b])
def judge(self,point):
return point[1]*(self.w*point[0].T+self.b)
def train(self):
flag = True
while(flag):
count = 0
for point in self.train_set:
if(self.judge(point)<=0):
self.update(point)
else:
count += 1
if(count == len(self.train_set)):
flag = False
def show():
print("參數w,b更新過程:",perceptron.history)
anim = animation.FuncAnimation(fig, animate, init_func=init, frames=len(perceptron.history),
interval=1000, repeat=False,blit=True)
plt.show()

限於篇幅,完整代碼可以通過下方名片聯系我獲取
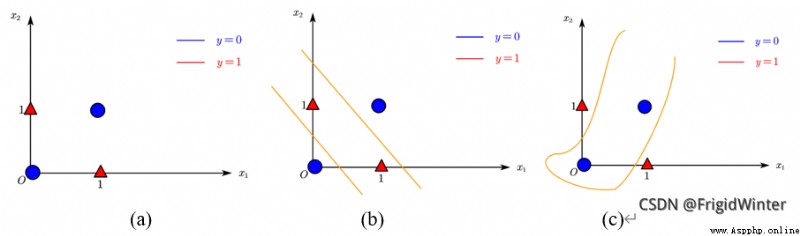
感知機最大的缺陷在於其線性,單個感知機只能表達一條直線,即使是如圖(a)所示簡單的異或門樣本,都無法進行分類。對此有兩種解決方式:
更多精彩專欄: