目錄
1、原理
2、案例
3、Python實現
4、結果
5、展望

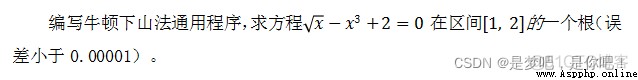
import numpy as np
# Store the iteration value of each step
result = []
# Store downhill factors for each step
all_r = []
# Judge whether it is singular. True is singular and false is nonsingular
def strange(xk):
return True if (0.5*xk**(-1/2)-3*xk**2) == 0 else False
# Primitive function
def fx(xk):
return xk**(1/2)-xk**3+2
# Newton iterative formula
# xk is the iterative value and r is the downhill factor
def nd(xk, r):
return xk - fx(xk) / (0.5*xk**(-1/2)-3*xk**2) * r
# Newton downhill formula
# return True Downhill success False Downhill failure
def nd_xs(xk, m):
r = 1
count = 1
while True:
if count > m:
return False
xk1 = nd(xk, r)
if abs(fx(xk1)) < abs(fx(xk)):
result.append(xk1)
all_r.append(r)
return True
else:
r *= 0.5
count += 1
# Main function
def main():
# initial value
x = float(input("Please enter the initial value:"))
result.append(x)
# Error limit
e = float(input("Please enter the error limit:"))
# Maximum number of iterations
n = int(input("Please enter the maximum number of iterations:"))
# Maximum number of downhill
m = int(input("Please enter the maximum number of times to go down the mountain:"))
# Number of iterations
ite = 1
while True:
if ite > n:
print("Number of iterations exceeded!")
return
if strange(result[-1]):
print("Singular, denominator zero!")
return
if not nd_xs(result[-1], m):
print("Downhill failure!")
return
if abs(result[-1] - result[-2]) < e:
print("Downhill factor of each step:" + str(all_r))
print("Iteration value of each step (including initial value):" + str(result))
return
ite += 1
if __name__ =='__main__':
main()
Please enter the initial value:1.5
Please enter the error limit:0.00001
Please enter the maximum number of iterations:100000
Please enter the maximum number of times to go down the mountain:100000
Downhill factor of each step:[1, 1, 1]
Iteration value of each step (including initial value):[1.5, 1.4763069991556952, 1.4758905899820982, 1.4758904626019806]
