1 題目

找出所有相加之和為 n 的 k 個數的組合，且滿足下列條件：

只使用數字1到9
每個數字 最多使用一次
返回 所有可能的有效組合的列表 。該列表不能包含相同的組合兩次，組合可以以任何順序返回。

示例 1:

輸入: k = 3, n = 7
輸出: [[1,2,4]]
解釋:
1 + 2 + 4 = 7
沒有其他符合的組合了。

示例 2:

輸入: k = 3, n = 9
輸出: [[1,2,6], [1,3,5], [2,3,4]]
解釋:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
沒有其他符合的組合了。

2 解析

主要需要解決的就是數組元素存在重復情況的問題，下面是解決的辦法：

首先先將數組進行排序，這樣重復的元素位置相鄰，可以快速去重；
因為不允許組合重復（相同數字不同排序視為重復），所以遞歸每層不能存在重復的元素。
為了避免重復選擇同個元素，進入下層遞歸時，選擇下一個索引位置對應的元素。
這裡用一個簡單圖示來加深理解，如下：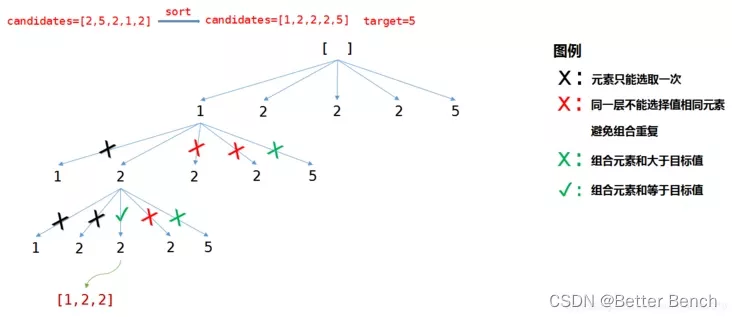

和40.題組合總和 II一樣的思路，多了一個判斷條件，就是對列表的長度限制

3 Python實現

class Solution:
def combinationSum3(self, k: int, n: int) -> List[List[int]]:
candidates = list(range(1,10))
target = n
# 結果列表
ans = []
# 可能組合
tmp = []
def back_dfs(idx, total):
# 判斷長度和值是否達到要求
if total == target and len(tmp[::])==k:
ans.append(tmp[::])
return
if total > target:
return
for i in range(idx, len(candidates)):
# 這裡限制同一層不能選擇值相同的元素
# 若有相同的元素，優先選擇索引靠前的
if candidates[i-1] == candidates[i] and i-1 >= idx:
continue
total += candidates[i]
tmp.append(candidates[i])
# 從當前索引的下一位開始選取，避免重復選取同個元素
back_dfs(i+1, total)
# 回溯
tmp.pop()
total -= candidates[i]
total = 0
back_dfs(0, total)
return ans