用python解決微分方程

一.用python求解一階常微分方程

標准形式：

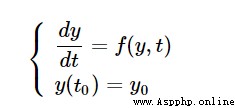
准備工作：

1.首先需要導入scipy庫，只需在終端輸入pip install scipy然後回車即可

同理導入numpy，matplotlib 包

2. scipy.integrate.odeint()是求解的具體方法，這個函數完整版是這樣的

scipy.integrate.odeint(func, y0, t, args=(), Dfun=None, col_deriv=0, full_output=0, ml=None, mu=None, rtol=None, atol=None, tcrit=None, h0=0.0, hmax=0.0, hmin=0.0, ixpr=0, mxstep=0, mxhnil=0, mxordn=12, mxords=5, printmessg=0, tfirst=False)

但是我們只需要用到前三個參數：

func : 導數函數f(y,t)，即y在t處的導數，用函數形式表示

y0 ：初始條件y0，用數組的形式表示

t : 求解函數值對應的時間點的序列。序列的第一個元素是與初始條件 y0 對應的初始時間 t0；時間序列必須是單調遞增或單調遞減的，允許重復值。

好啦，現在我們開始正式編程求解：

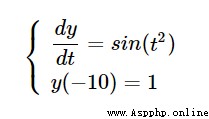
首先導入庫函數：

from scipy.integrate import odeint

import numpy as np

import matplotlib.pyplot as plt 

接著定義函數f(y,t):

def dy_dt(y,t):

    return np.sin(t**2)

使用odeint()方法：

y0=[1]

t = np.arange(-10,10,0.01)   #（start，stop，step）

y=odeint(dy_dt,y0,t)

最後就是繪圖啦：

plt.plot(t, y)

plt.title("picture")

plt.show()

完整代碼貼一貼：

from scipy.integrate import odeint
import numpy as np
import matplotlib.pyplot as plt
def dy_dt(y,t):
return np.sin(t**2)
y0=[1]
t = np.arange(-10,10,0.01)
y=odeint(dy_dt,y0,t)
plt.plot(t, y)
plt.title("picture")
plt.show()

得到結果：

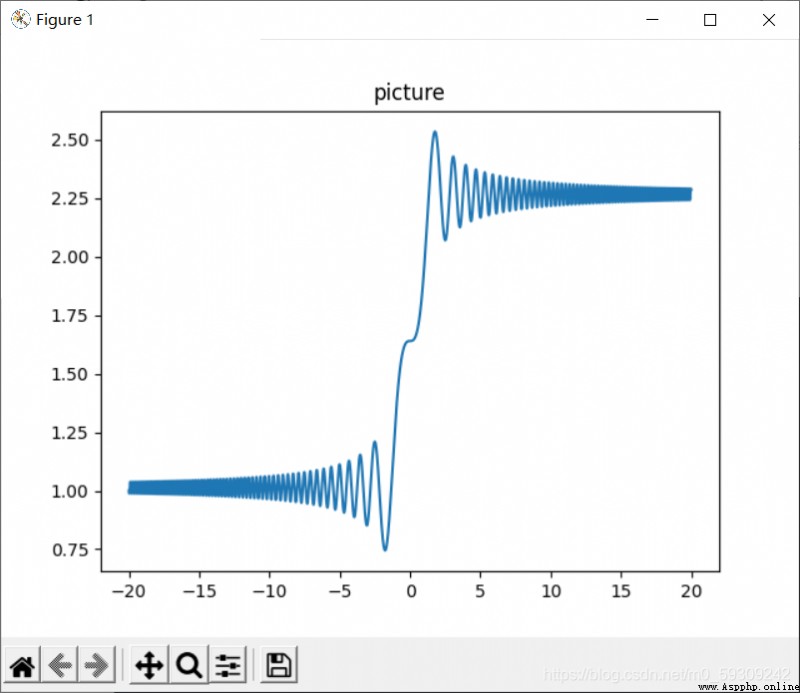
二.求解高階微分方程：

高階常微分方程，必須做變量替換，化為一階微分方程組，再用 odeint 求數值解

我們來看這個例子：

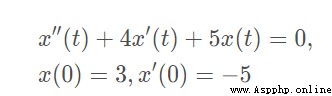
直接上代碼：

import matplotlib.pyplot as plt
from scipy import linspace,exp
from scipy.integrate import odeint
import numpy as np
def fvdp(t,y):
'''
要把y看出一個向量，y = [dy0,dy1,dy2,...]分別表示y的n階導，那麼
y[0]就是需要求解的函數，y[1]表示一階導，y[2]表示二階導，以此類推
'''
dy1 = y[1] # y[1]=dy/dt，一階導
dy2 = -4 * y[1] - 5* y[0]
# y[0]是最初始，也就是需要求解的函數
# 注意返回的順序是[一階導， 二階導]，這就形成了一階微分方程組
return [dy1,dy2]
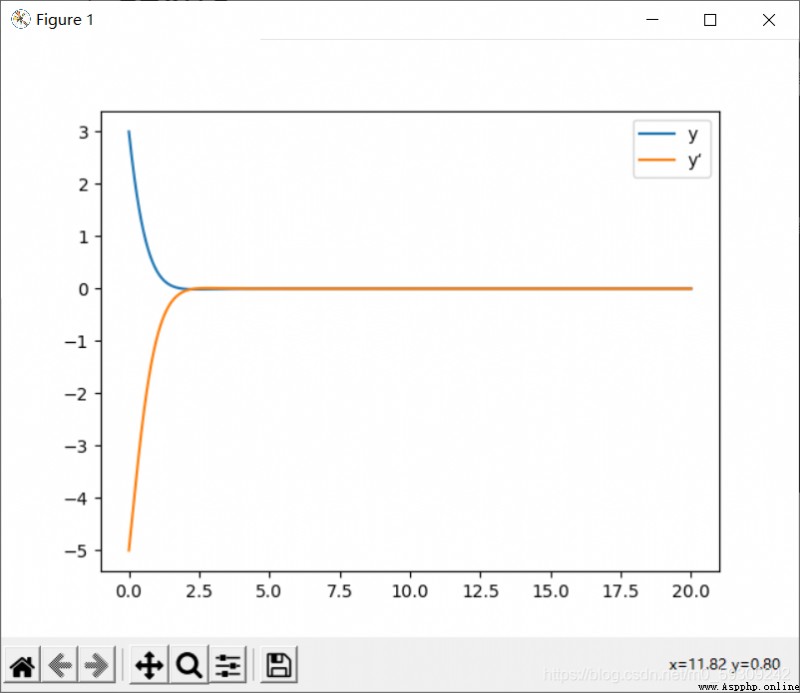
def solve_second_order_ode():
'''
求解二階ODE
'''
x = linspace(0,20,1000)#給x規定范圍
y0 = [3.0, -5.0] # 初值條件
# 初值[3.0, -5.0]表示y(0)=3,y'(0)=-5
# 返回y，其中y[:,0]是y[0]的值，就是最終解，y[:,1]是y'(x)的值
y = odeint(fvdp, y0, x, tfirst=True)
y1, = plt.plot(x,y[:,0],label='y')
y1_1, = plt.plot(x,y[:,1],label='y‘')
plt.legend(handles=[y1,y1_1]) #創建圖例
plt.show()
solve_second_order_ode()

 得到結果：