numpy.linalg 模塊包含線性代數的函數。使用這個模塊,可以計算逆矩陣、求特征值、解線性方程組以及求解行列式等。
一、計算逆矩陣
線性代數中,矩陣A與其逆矩陣A ^(-1)相乘後會得到一個單位矩陣I。該定義可以寫為A *A ^(-1) =1。numpy.linalg 模塊中的 inv 函數可以計算逆矩陣。
1) 用 mat 函數創建示例矩陣
import numpy as np
import matplotlib.pyplot as plt A = np.mat("0 1 2;1 0 3;4 -3 8")
2)用 inv 函數計算逆矩陣
inverse = np.linalg.inv(A)
print("inverse of A\n", inverse)
運行結果如下:
A
[[ 0 1 2]
[ 1 0 3]
[ 4 -3 8]]
inverse of A
[[-4.5 7. -1.5]
[-2. 4. -1. ]
[ 1.5 -2. 0.5]]
3)可能通過原矩陣和逆矩陣相乘的結果來驗證
print ("Check\n", A * inverse) #驗證計算,原矩陣和逆矩陣相乘的,單位矩陣結果:
Check
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]
二、求解線性方程組
線性議程組 Ax=b
1)分另創建矩陣A和數組b
A = np.mat("1 -2 1;0 2 -8;-4 5 9") #用mat()函數創建示例矩陣
print("A\n", A)
b = np.array([0, 8, -9])2)用solve(A, b)解出x,用dot()函數進行驗證,並打印
x = np.linalg.solve(A, b)
print("Solution", x)
print("Check\n", np.dot(A , x)) #用dot()函數檢查求得的解是否正確
三、特征值和特征向量
特征值(eigenvalue)即方程 Ax = ax 的根,是一個標量,特征向量是關於特征值的向量。在numpy.linalg 模塊中, eigvals函數可以計算矩陣的特征值,而 eig 函數可以返回一個包含特征值和對應的特征向量的元組。
用 eigvals 函數求解特征值
用 eig 函數求解特征值和特征向量 ,如下代碼:
print("Eigenvalues", np.linalg.eigvals(A))
eigenvalues, eigenvectors = np.linalg.eig(A)
print( "First tuple of eig", eigenvalues)
print(" Second tuple of eig\n", eigenvectors)四、奇異值分解
奇異值分解,是一種因子分解運算,將一個矩陣分解為3個矩陣的乘積。奇異值分解是特征值分解一種推廣。在 numpy.linalg 模塊中的svd()函數可以對矩陣進行奇異值分解。該函數返回3個矩陣——U、Sigma和V,其中U和V是正交矩陣,Sigma包含輸入矩陣的奇異值(計算出來結果可能是虛數)。
U, Sigma, V = np.linalg.svd(A, full_matrices=False)# 用svd() 函數分解矩陣
print ("U:",U)
print ("Sigma:",Sigma)
print ("V:", V)
print ("Product\n", U * np.diag(Sigma) * V) #用diag函數生成完整的奇異值矩陣
五、廣義
pinv 函數進行求解,計算廣義逆矩陣需要用到奇異值分解函數pinv(),行列式計算用np.linalg中的函數det():
#使用pinv函數計算廣義逆矩陣:
A = np.mat("4 11 14;8 7 -2")
pseudoinv = np.linalg.pinv(A)
print("Pseudo inverse:\n", pseudoinv)
#計算矩陣的行列式
print("\n")
B = np.mat("3 4;5 6")
print("Determinant:", np.linalg.det(B))
全部代碼如下:
import numpy as np
import matplotlib.pyplot as plt A = np.mat("0 1 2;1 0 3;4 -3 8") #用mat()函數創建示例矩陣
print ("A\n",A)
inverse = np.linalg.inv(A) #用inv()函數計算逆矩陣
print("inverse of A\n", inverse)
print ("Check\n", A * inverse) #驗證計算,原矩陣和逆矩陣相乘的,單位矩陣
# 求解線性方程組
A = np.mat("1 -2 1;0 2 -8;-4 5 9") #用mat()函數創建示例矩陣
b = np.array([0, 8, -9])
x = np.linalg.solve(A, b)
print("Solution", x)
print("Check\n", np.dot(A , x)) #用dot()函數檢查求得的解是否正確
#特征值和特征向量 print("Eigenvalues", np.linalg.eigvals(A)) #eigvals函數可以計算矩陣的特征值
eigenvalues, eigenvectors = np.linalg.eig(A) #用 eig 函數求解特征值和特征向量
print( "First tuple of eig", eigenvalues)
print(" Second tuple of eig\n", eigenvectors) #奇異值分解
U, Sigma, V = np.linalg.svd(A, full_matrices=False)# 用svd() 函數分解矩陣
print ("U:",U)
print ("Sigma:",Sigma)
print ("V:", V)
print ("Product\n", U * np.diag(Sigma) * V) #用diag函數生成完整的奇異值矩陣
#使用pinv函數計算廣義逆矩陣:
A = np.mat("4 11 14;8 7 -2")
pseudoinv = np.linalg.pinv(A)
print("Pseudo inverse:\n", pseudoinv)
#計算矩陣的行列式
print("\n")
B = np.mat("3 4;5 6")
print("Determinant:", np.linalg.det(B))
運行結果:
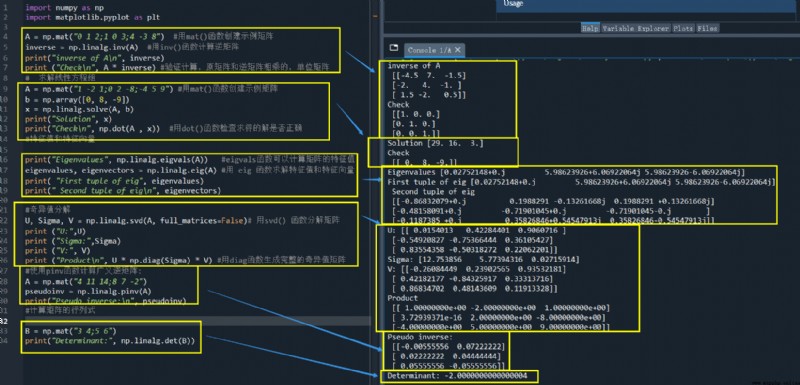
本篇介紹了一些numpy.linalg 模塊中常用的函數,
摘要:本篇我們將以分析歷史股價為例,介紹怎樣從文件中載入數據,以及怎樣使用NumPy的基本數學和統計分析函數.學習讀寫文件的方法,並嘗試函數式編程和NumPy線性代數運算,來學習NumPy的常用函數. ...
摘要:總結股票均線計算原理--線性關系,也是以後大數據處理的基礎之一,NumPy的 linalg 包是專門用於線性代數計算的.作一個假設,就是一個價格可以根據N個之前的價格利用線性模型計算得出. 前一 ...
摘要:NumPy中包含大量的函數,這些函數的設計初衷是能更方便地使用,掌握解這些函數,可以提升自己的工作效率.這些函數包括數組元素的選取和多項式運算等.下面通過實例進行詳細了解. 前述通過對某公司股票 ...
在NumPy中,矩陣是 ndarray 的子類,與數學概念中的矩陣一樣,NumPy中的矩陣也是二維的,可以使用 mat . matrix 以及 bmat 函數來創建矩陣. 一.創建矩陣 mat 函數創 ...
成交量(volume)是投資中一個非常重要的變量,它是指在某一時段內具體的交易數,可以在分時圖中繪制,包括日線圖.周線圖.月線圖甚至是5分鐘.30分鐘.60分鐘圖中繪制. 股票市場成交量的變化反映了資 ...
摘要:先匯總相關股票價格,然後有選擇地對其分類,再計算移動均線.布林線等. 一.匯總數據 匯總整個交易周中從周一到周五的所有數據(包括日期.開盤價.最高價.最低價.收盤價,成交量等),由於我們的數據是 ...
在NumPy中,所有的標准三角函數如sin.cos.tan等均有對應的通用函數. 一.利薩茹曲線 (Lissajous curve)利薩茹曲線是一種很有趣的使用三角函數的方式(示波器上顯示出利薩茹曲線 ...
Numpy介紹: NumPy是高性能科學計算和數據分析的基礎包.它是pandas等其他各種工具的基礎. NumPy的主要功能: 1)ndarray,一個多維數組結構,高效且節省空間 2)無需循環對整組 ...
前言 本文的文字及圖片來源於網絡,僅供學習.交流使用,不具有任何商業用途,版權歸原作者所有,如有問題請及時聯系我們以作處理. 作者:基因學苑 NumPy(Numerical Python的簡稱)是高性 ...
目錄numpy常用函數學習點乘法線型預測線性擬合裁剪.壓縮和累乘相關性多項式擬合提取符號數組雜項點乘法該方法為數學方法,但是在numpy使用的時候略坑.numpy的點乘為a.dot(b)或numpy. ...
typeof 它返回值是一個字符串,該字符串說明運算數的類型. a=1; b=true; c="c"; d=function(){ console.log(" ...
今天下午程序寫完,有些時間就搞下界面美化,做個無框窗體.首先把窗體的FormBorderStyle設置為None,就變成無框的啦,不過你會發現這樣窗體上就沒有原來的最大最小化和關閉按鈕了哦,所以要自己 ...
前言 數據庫系統與文件系統最大的區別在於數據庫能保證操作的原子性,一個操作要麼不做要麼都做,即使在數據庫宕機的情況下,也不會出現操作一半的情況,這個就需要數據庫的日志和一套完善的奔潰恢復機制來保證.本 ...
具體實例 1.PHP 服務器組件 對於初學者建議使用集成的服務器組件,它已經包含了 PHP.Apache.Mysql 等服務,免去了開發人員將時間花費在繁瑣的配置環境過程. Window 系統可以使用 ...
和大多數配置文件一樣,log4j配置文件也有key-value形式和xml形式.這裡主要記錄一下key-value的形式 我們通過配置,可以創建出Log4j的運行環境.Log4j由三個重要的組件構成: ...
You are given coins of different denominations and a total amount of money amount. Write a function ...
在vue1.0中,組件之間的通信主要通過vm.$dispatch沿著父鏈向上傳播和用vm.$broadcast向下廣播來實現.然而在vue2.0中,已經廢除了這種用法. vuex加入後,對組件之間的通 ...
DailyRollingFileAppender是日志記錄軟件包Log4J中的一個Appender,它能夠按一定的頻度滾動日志記錄文件. 我們可以按下面的方式配置DailyRollingFileApp ...
我們首先看下面的代碼 data = { "siteName" : "西部雲谷二期17", "PM10" : "10017" ...
先來操作函數部分,普遍的MySQL 函數方法,但隨著PHP5的發展,有些函數使用的要求加重了,有些則將廢棄不用,有些則參數必填... ================================= ...