- 本文是個人快速入門OpenCV-Python的電子筆記,由於水平有限,難免出現錯漏,敬請批評改正。
import cv2
import numpy as np
import matplotlib.pyplot as plt
img1=cv2.imread("1.jpg",0)
img1_resize=cv2.resize(img1,(400,400))
''' hist = cv2.calcHist( images, channels, mask, histSize, ranges, accumulate ) 參數說明: hist:返回的統計直方圖,是一個一維數組,數組內的元素是各個灰度級的像素個數。 images:原始圖像,該圖像需要使用“[ ]”括起來。 channels:指定通道編號。通道編號需要用“[ ]”括起來, 如果輸入圖像是單通道灰度圖像,該參數的值就是[0]。 對於彩色圖像,它的值可以是[0]、[1]、[2],分別對應通道B、G、R。 mask:掩模圖像。當統計整幅圖像的直方圖時,將這個值設為 None。 當統計圖像某一部分的直方圖時,需要用到掩模圖像。 histSize:BINS 的值,該值需要用“[ ]”括起來。 例如,BINS 的值是 256,需要使用“[256]”作為此參數值。 ranges:即像素值范圍。例如,8 位灰度圖像的像素值范圍是[0, 255]。 accumulate:累計(累積、疊加)標識,默認值為 False。 如果被設置為 True,則直方圖 在開始計算時不會被清零,計算的是多個直方圖的累積結果, 用於對一組圖像計算直方圖。 該參數允許從多個對象中計算單個直方圖,或者實時更新直方圖。 該參數是可選的,一般情況下不需要設置。 '''
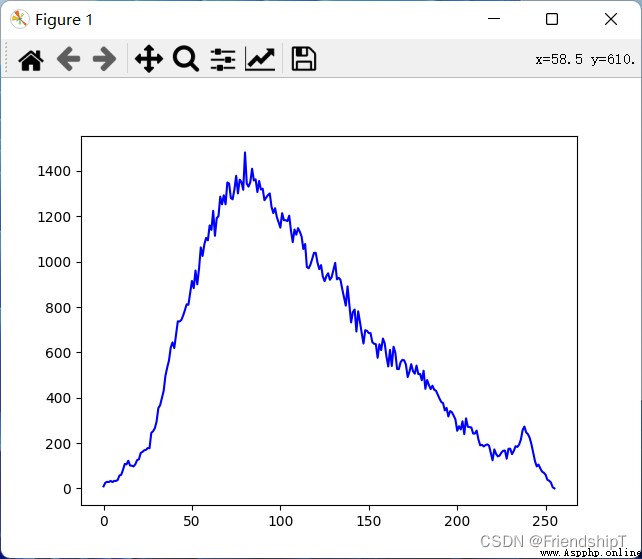
hist = cv2.calcHist([img1_resize],[0],None,[256],[0,255])
plt.plot(hist,color='b')
plt.show()
import cv2
import numpy as np
import matplotlib.pyplot as plt
img1=cv2.imread("1.jpg")
img1_resize=cv2.resize(img1,(400,400))
''' hist = cv2.calcHist( images, channels, mask, histSize, ranges, accumulate ) 參數說明: hist:返回的統計直方圖,是一個一維數組,數組內的元素是各個灰度級的像素個數。 images:原始圖像,該圖像需要使用“[ ]”括起來。 channels:指定通道編號。通道編號需要用“[ ]”括起來, 如果輸入圖像是單通道灰度圖像,該參數的值就是[0]。 對於彩色圖像,它的值可以是[0]、[1]、[2],分別對應通道B、G、R。 mask:掩模圖像。當統計整幅圖像的直方圖時,將這個值設為 None。 當統計圖像某一部分的直方圖時,需要用到掩模圖像。 histSize:BINS 的值,該值需要用“[ ]”括起來。 例如,BINS 的值是 256,需要使用“[256]”作為此參數值。 ranges:即像素值范圍。例如,8 位灰度圖像的像素值范圍是[0, 255]。 accumulate:累計(累積、疊加)標識,默認值為 False。 如果被設置為 True,則直方圖 在開始計算時不會被清零,計算的是多個直方圖的累積結果, 用於對一組圖像計算直方圖。 該參數允許從多個對象中計算單個直方圖,或者實時更新直方圖。 該參數是可選的,一般情況下不需要設置。 '''
histb = cv2.calcHist([img1_resize],[0],None,[256],[0,255])
histg = cv2.calcHist([img1_resize],[1],None,[256],[0,255])
histr = cv2.calcHist([img1_resize],[2],None,[256],[0,255])
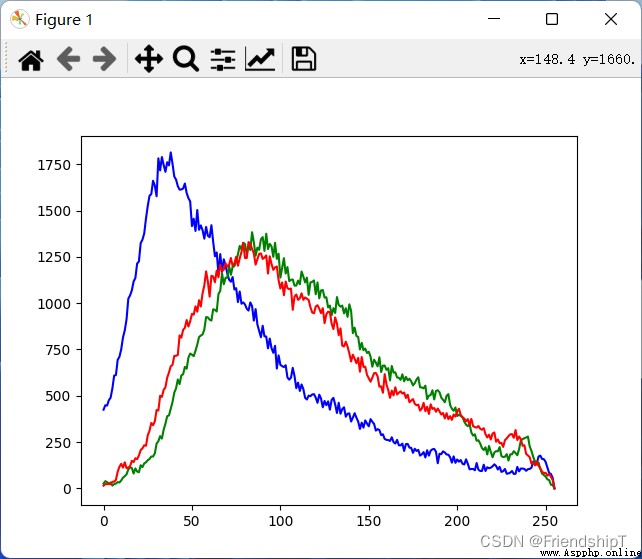
plt.plot(histb,color='b')
plt.plot(histg,color='g')
plt.plot(histr,color='r')
plt.show()
- 如果一幅圖像擁有全部可能的灰度級,並且像素值的灰度均勻分布,那麼這幅圖像就具有高對比度和多變的灰度色調,灰度級豐富且覆蓋范圍較大。在外觀上,這樣的圖像具有更豐富的色彩,不會過暗或過亮。
- 直方圖均衡化的主要目的是將原始圖像的灰度級均勻地映射到整個灰度級范圍內,得到一個灰度級分布均勻的圖像。這種均衡化,既實現了灰度值統計上的概率均衡,也實現了人類視覺系統(Human Visual System,HVS)上的視覺均衡。
- 直方圖均衡化的算法主要包括兩個步驟:
(1)計算累計直方圖。
(2)對累計直方圖進行區間轉換
在此基礎上,再利用人眼視覺達到直方圖均衡化的目的。- 例如,一張3×3圖像img,它是一幅 3 位的位圖,即共有 4= 2 2 2^2 22個灰度級,具有9像素: [ 1 1 3 2 3 2 2 1 0 ] \left[ \begin{matrix} 1 & 1 & 3\\ 2 & 3 & 2 \\ 2 & 1 & 0 \end{matrix} \right] ⎣⎡122131320⎦⎤
- 圖像img的統計直方圖,如下表所示。
灰度級(像素值) 0 1 2 3 像素個數1332
- 計算歸一化統計直方圖,計算方式是計算每個像素在圖像內出現的概率。 出現概率 = 出現次數 像素總數 出現概率=\frac{出現次數}{像素總數} 出現概率=像素總數出現次數,用每個灰度級的像素個數除以總的像素個數(9),就得到歸一化統計直方圖,如下表所示。
灰度級(像素值) 0 1 2 3 概率 1 9 \frac{1}{9} 91 1 3 \frac{1}{3} 31 1 3 \frac{1}{3} 31 2 9 \frac{2}{9} 92
- 計算累計統計直方圖,即計算所有灰度級的累計概率,如下表所示。
灰度級(像素值) 0 1 2 3 累計概率 1 9 \frac{1}{9} 91 1 9 + 1 3 = 4 9 \frac{1}{9}+\frac{1}{3}=\frac{4}{9} 91+31=94 4 9 + 1 3 = 7 9 \frac{4}{9}+\frac{1}{3}=\frac{7}{9} 94+31=97 7 9 + 2 9 = 1 \frac{7}{9}+\frac{2}{9}=1 97+92=1
- 計算均衡化後的直方圖,常見的方式有兩種,一種是在原有范圍內實現直方圖均衡化時,用當前灰度級的累計概率乘以當前灰度級的最大值,另一種是在更廣泛的范圍內實現直方圖均衡化時,用當前灰度級的累計概率乘以更廣泛范圍灰度級的最大值,得到新的灰度級,並作為均衡化的結果。如下表所示。
灰度級(像素值) 0 1 2 3 像素個數1332累計概率 1 9 \frac{1}{9} 91 4 9 \frac{4}{9} 94 7 9 \frac{7}{9} 97 1 1 1原始范圍均衡化(新的灰度級) 3 × 1 9 ≈ 0 3\times\frac{1}{9}\approx0 3×91≈0 3 × 4 9 ≈ 1 3×\frac{4}{9}\approx1 3×94≈1 3 × 7 9 ≈ 2 3×\frac{7}{9}\approx2 3×97≈2 3 × 1 = 3 3×1=3 3×1=3[0,255]范圍均衡化(新的灰度級) 255 × 1 9 ≈ 28 255\times\frac{1}{9}\approx28 255×91≈28 3 × 4 9 ≈ 113 3×\frac{4}{9}\approx113 3×94≈113 255 × 7 9 ≈ 198 255×\frac{7}{9}\approx198 255×97≈198 255 × 1 = 255 255×1=255 255×1=255
import cv2
import numpy as np
import matplotlib.pyplot as plt
img1=cv2.imread("1.jpg",0)
img1_resize=cv2.resize(img1,(400,400))
# 直方圖均衡化處理dst = cv2.equalizeHist(src)
equ = cv2.equalizeHist(img1_resize)
# 顯示均衡化前後的圖像
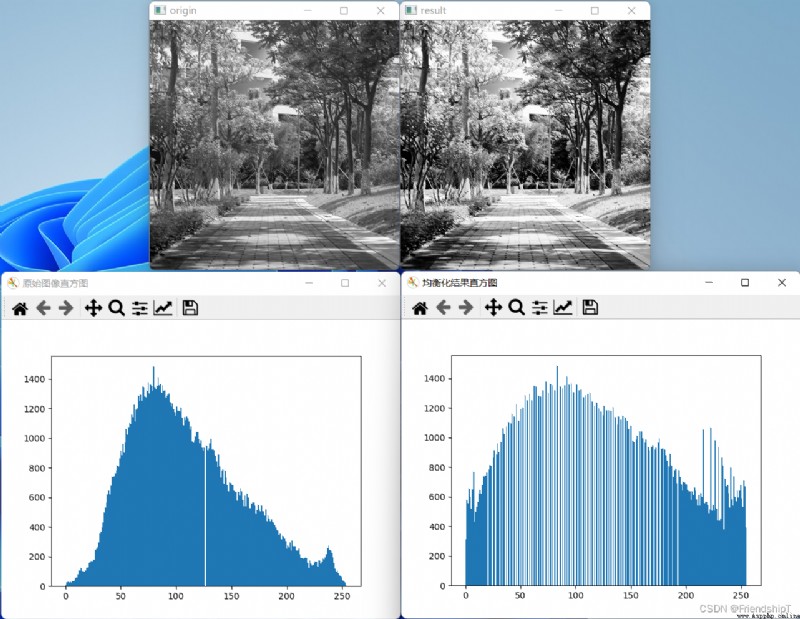
cv2.imshow("origin",img1_resize)
cv2.imshow("result",equ)
''' plt.hist(X,BINS) 參數說明: X:數據源,必須是一維的。圖像通常是二維的, 需要使用 ravel()函數將圖像處理為一維數據源以後,再作為參數使用。 BINS:BINS 的具體值,表示灰度級的分組情況。 函數 ravel()的作用是將二維數組降維成一維數組 '''
# 顯示均衡化前後的直方圖
plt.figure("原始圖像直方圖") #構建窗口
plt.hist(img1_resize.ravel(),256)
plt.figure("均衡化結果直方圖") #構建新窗口
plt.hist(equ.ravel(),256)
plt.show()
# 等待釋放窗口
cv2.waitKey()
cv2.destroyAllWindows()
[1] https://opencv.org/
[2] 李立宗. OpenCV輕松入門:面向Python. 北京: 電子工業出版社,2019
- 更多精彩內容,可點擊進入
OpenCV-Python快速入門專欄或我的個人主頁查看