我們也可以利用二叉搜索樹的性質:對於某一個節點若是p與q都小於等於這個這個節點值,說明p、q都在這個節點的左子樹,而最近的公共祖先也一定在這個節點的左子樹;若是p與q都大於等於這個節點,說明p、q都在這個節點的右子樹,而最近的公共祖先也一定在這個節點的右子樹。而若是對於某個節點,p與q的值一個大於等於節點值,一個小於等於節點值,說明它們分布在該節點的兩邊,而這個節點就是最近的公共祖先,因此從上到下的其他祖先都將這個兩個節點放到同一子樹,只有最近公共祖先會將它們放入不同的子樹,每次進入一個子樹又回到剛剛的問題,因此可以使用遞歸。
step 1:首先檢查空節點,空樹沒有公共祖先。
step 2:對於某個節點,比較與p、q的大小,若p、q在該節點兩邊說明這就是最近公共祖先。
step 3:如果p、q都在該節點的左邊,則遞歸進入左子樹。
step 4:如果p、q都在該節點的右邊,則遞歸進入右子樹。
class Solution:
def lowestCommonAncestor(self , root: TreeNode, p: int, q: int) -> int:
if root is None:
return -1
if (p >= root.val and q <= root.val) or (p <= root.val and q >= root.val):
return root.val
elif p <= root.val and q <= root.val:
return self.lowestCommonAncestor(root.left, p, q)
else:
return self.lowestCommonAncestor(root.right, p, q)
時間復雜度:O(n),設二叉樹共有 n 個節點,最壞情況遞歸遍歷所有節點。
空間復雜度:O(n),遞歸棧深度最壞為 n。
step 1:根據二叉搜索樹的性質,從根節點開始查找目標節點,當前節點比目標小則進入右子樹,當前節點比目標大則進入左子樹,直到找到目標節點。這個過程成用數組記錄遇到的元素。
step 2:分別在搜索二叉樹中找到p和q兩個點,並記錄各自的路徑為數組。
step 3:同時遍歷兩個數組,比較元素值,最後一個相等的元素就是最近的公共祖先。
class Solution:
def getPath(self, root: TreeNode, p: int):
path = []
while p != root.val:
path.append(root.val)
if p < root.val:
root = root.left
else:
root = root.right
path.append(root.val)
return path
def lowestCommonAncestor(self , root: TreeNode, p: int, q: int) -> int:
path1 = self.getPath(root, p)
path2 = self.getPath(root, q)
i = 0
# 最後一個相同的節點就是最近公共祖先
while i < len(path1) and i < len(path2):
if path1[i] == path2[i]:
res = path1[i]
i = i + 1
else:
break
return res
時間復雜度: O ( n ) O(n) O(n),設二叉樹共有 n 個節點,因此最壞情況二叉搜索樹變成鏈表,搜索到目標節點需要 O(n),比較路徑前半段的相同也需要 O(n)。
空間復雜度: O ( n ) O(n) O(n),記錄路徑的數組最長為 n。
既然要找到二叉樹中兩個節點的最近公共祖先,那我們可以考慮先找到兩個節點全部祖先,可以得到從根節點到目標節點的路徑,然後依次比較路徑得出誰是最近的祖先。找到兩個節點的所在可以深度優先搜索遍歷二叉樹所有節點進行查找。
step 1:利用dfs求得根節點到兩個目標節點的路徑:每次選擇二叉樹的一棵子樹往下找,同時路徑數組增加這個遍歷的節點值。
step 2:一旦遍歷到了葉子節點也沒有,則回溯到父節點,尋找其他路徑,回溯時要去掉數組中剛剛加入的元素。
step 3:然後遍歷兩條路徑數組,依次比較元素值。
step 4:找到兩條路徑第一個不相同的節點即是最近公共祖先
class Solution:
# 記錄是否找到到達o的路徑
flag = False
# 求根節點到目標節點的路徑,不同於二叉搜索樹
def dfs(self, root: TreeNode, path: List[int], o: int):
if root is None or self.flag:
return
path.append(root.val)
if root.val == o:
self.flag = True
return
# dfs遍歷查找
self.dfs(root.left, path, o)
self.dfs(root.right, path, o)
# 找到
if self.flag:
return
# 該子樹沒有,回溯
path.pop()
def lowestCommonAncestor(self , root: TreeNode, o1: int, o2: int) -> int:
path1 = []
path2 = []
# 求根節點到兩個節點的路徑
self.dfs(root, path1, o1)
# 重置flag,查找下一個
self.flag = False
self.dfs(root, path2, o2)
i = 0
# 最後一個相同的節點就是最近公共祖先
while i < len(path1) and i < len(path2):
if path1[i] == path2[i]:
res = path1[i]
i = i + 1
else:
break
return res
時間復雜度:O(n),其中 n 為二叉樹節點數,遞歸遍歷二叉樹每一個節點求路徑,後續又遍歷路徑。
空間復雜度:O(n),最壞情況二叉樹化為鏈表,深度為 n,遞歸棧深度和路徑數組為 n。
step 1:如果o1和o2中的任一個和root匹配,那麼root就是最近公共祖先。
step 2:如果都不匹配,則分別遞歸左、右子樹。
step 3:如果有一個節點出現在左子樹,並且另一個節點出現在右子樹,則root就是最近公共祖先.
step 4:如果兩個節點都出現在左子樹,則說明最低公共祖先在左子樹中,否則在右子樹。
step 5:繼續遞歸左、右子樹,直到遇到step1或者step3的情況。
class Solution:
def lowestCommonAncestor(self , root: TreeNode, o1: int, o2: int) -> int:
# 該子樹沒找到,返回-1
if root is None:
return -1
# 該節點是其中某一個節點
if o1 == root.val or o2 == root.val:
return root.val
# 左子樹尋找公共祖先
left = self.lowestCommonAncestor(root.left, o1, o2)
# 右子樹尋找公共祖先
right = self.lowestCommonAncestor(root.right, o1, o2)
# 左子樹為沒找到,則在右子樹中
if left == -1:
return right
# 右子樹沒找到,則在左子樹中
if right == -1:
return left
# 否則是當前節點
return root.val
時間復雜度:O(n),其中 n 為節點數,遞歸遍歷二叉樹每一個節點。
空間復雜度:O(n),最壞情況二叉樹化為鏈表,遞歸棧深度為 n。
序列化即將二叉樹的節點值取出,放入一個字符串中,我們可以按照前序遍歷的思路,遍歷二叉樹每個節點,並將節點值存儲在字符串中,我們用‘#’表示空節點,用‘!'表示節點與節點之間的分割。
反序列化即根據給定的字符串,將二叉樹重建,因為字符串中的順序是前序遍歷,因此我們重建的時候也是前序遍歷,即可還原。
step 1:優先處理序列化,首先空樹直接返回“#”,然後調用SerializeFunction函數前序遞歸遍歷二叉樹。
SerializeFunction(root, res);
step 2:SerializeFunction函數負責前序遞歸,根據“根左右”的訪問次序,優先訪問根節點,遇到空節點在字符串中添加 ‘#’,遇到非空節點,添加相應節點數字和 ‘!’,然後依次遞歸進入左子樹,右子樹。
# 根節點
str.append(root.val).append('!');
# 左子樹
SerializeFunction(root.left, str);
# 右子樹
SerializeFunction(root.right, str);
step 3:創建全局變量 index 表示序列中的下標(C++中直接指針完成)。
step 4:再處理反序列化,讀入字符串,如果字符串直接為 “#”,就是空樹,否則還是調用DeserializeFunction函數前序遞歸建樹。
TreeNode res = DeserializeFunction(str);
step 5:DeserializeFunction函數負責前序遞歸構建樹,遇到‘#’則是空節點,遇到數字則根據感歎號分割,將字符串轉換為數字後加入新創建的節點中,依據 “根左右”,創建完根節點,然後依次遞歸進入左子樹、右子樹創建新節點。
TreeNode root = new TreeNode(val);
......
# 反序列化與序列化一致,都是前序
root.left = DeserializeFunction(str);
root.right = DeserializeFunction(str);

import sys
sys.setrecursionlimit(100000)
class Solution:
def __init__(self):
self.index = 0
self.s = ""
# 處理序列化
def SerializeFunction(self, root):
# 空節點
if not root:
self.s = self.s + '#'
return
# 根節點
self.s = self.s + str(root.val) + '-'
# 左子樹
self.SerializeFunction(root.left)
# 右子樹
self.SerializeFunction(root.right)
def Serialize(self, root):
if not root:
return '#'
self.s = ""
self.SerializeFunction(root)
return self.s
# 處理反序列化的功能函數
def DeserializeFunction(self, s: str):
# 到達葉節點時,構建完畢,返回繼續構建父節點
# 空節點
if self.index >= len(s) or s[self.index] == '#':
self.index = self.index + 1
return None
# 數字轉換
val = 0
while s[self.index] != '-' and self.index != len(s):
val = val * 10 + int(s[self.index])
self.index = self.index + 1
root = TreeNode(val)
# 序列到底了,構建完成
if self.index == len(s):
return root
else:
self.index = self.index + 1
root.left = self.DeserializeFunction(s)
root.right = self.DeserializeFunction(s)
return root
def Deserialize(self, s):
if s == '#':
return None
return self.DeserializeFunction(s)
時間復雜度:O(n),其中n為二叉樹節點數,前序遍歷,每個節點遍歷一遍。
空間復雜度:O(n),最壞情況下,二叉樹退化為鏈表,遞歸棧最大深度為n。
step 1:先根據前序遍歷第一個點建立根節點。
step 2:然後遍歷中序遍歷找到根節點在數組中的位置。
step 3:再按照子樹的節點數將兩個遍歷的序列分割成子數組,將子數組送入函數建立子樹。
step 4:直到子樹的序列長度為 0,結束遞歸。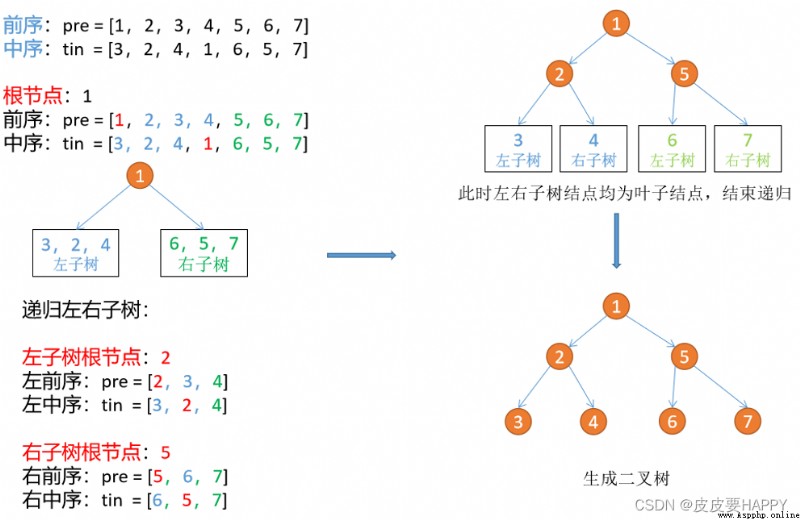
class Solution:
def reConstructBinaryTree(self , pre: List[int], vin: List[int]) -> TreeNode:
n = len(pre)
m = len(vin)
if n == 0 or m == 0:
return None
root = TreeNode(pre[0])
for i in range(len(vin)):
if pre[0] == vin[i]:
left_pre = pre[1:i+1]
left_vin = vin[:i]
root.left = self.reConstructBinaryTree(left_pre, left_vin)
right_pre = pre[i+1:]
right_vin = vin[i+1:]
root.right = self.reConstructBinaryTree(right_pre, right_vin)
break
return root
時間復雜度: O ( n ) O(n) O(n),其中 n 為數組長度,即二叉樹的節點數,構建每個節點進一次遞歸,遞歸中所有的循環加起來一共 n 次。
空間復雜度: O ( n ) O(n) O(n),遞歸棧最大深度不超過 n,輔助數組長度也不超過 n,重建的二叉樹空間屬於必要空間,不屬於輔助空間。
借助棧來解決問題需要關注一個問題,就是前序遍歷挨著的兩個值比如m和n,它們會有下面兩種情況之一的關系。
1、n是m左子樹節點的值。
2、n是m右子樹節點的值或者是m某個祖先節點的右節點的值。
對於第一種情況很容易理解,如果m的左子樹不為空,那麼n就是m左子樹節點的值。
對於第二種情況,如果一個結點沒有左子樹只有右子樹,那麼n就是m右子樹節點的值,如果一個結點既沒有左子樹也沒有右子樹,那麼n就是m某個祖先節點的右節點,只要找到這個祖先節點就可以。
step 1:首先前序遍歷第一個數字依然是根節點,並建立棧輔助遍歷。
step 2:然後我們就開始判斷,在前序遍歷中相鄰的兩個數字必定是只有兩種情況:要麼前序後一個是前一個的左節點;要麼前序後一個是前一個的右節點或者其祖先的右節點。
step 3:我們可以同時順序遍歷pre和vin兩個序列,判斷是否是左節點,如果是左節點則不斷向左深入,用棧記錄祖先,如果不是需要彈出棧回到相應的祖先,然後進入右子樹,整個過程類似非遞歸前序遍歷。
class Solution:
def reConstructBinaryTree(self , pre: List[int], vin: List[int]) -> TreeNode:
n = len(pre)
m = len(vin)
if n == 0 or m == 0:
return None
s = []
root = TreeNode(pre[0])
cur = root
j = 0
for i in range(1,n):
# 後一個是前一個的左孩子
if cur.val != vin[j]:
cur.left = TreeNode(pre[i])
s.append(cur)
cur = cur.left
# 後一個是前一個的右孩子,或者祖先的右孩子
else:
# 找到合適的cur,然後確定他的右孩子
j = j + 1
# 彈出到符合的祖先
while s and s[-1].val == vin[j]:
cur = s.pop()
j = j + 1
# 給cur添加右節點
cur.right = TreeNode(pre[i])
cur = cur.right
return root
時間復雜度:O(n),其中 n 為數組長度,即二叉樹的節點數,遍歷一次數組,彈出棧的循環最多進行n次。
空間復雜度:O(n),棧空間最大深度為 n,重建的二叉樹空間屬於必要空間,不屬於輔助空間。
首先建樹方面,前序遍歷是根左右的順序,中序遍歷是左根右的順序,因為節點值互不相同,我們可以根據在前序遍歷中找到根節點(每個子樹部分第一個就是),再在中序遍歷中找到對應的值,從其左右分割開,左邊就是該樹的左子樹,右邊就是該樹的右子樹,於是將問題劃分為了子問題。
而打印右視圖即找到二叉樹每層最右邊的節點元素,我們可以采取dfs(深度優先搜索)遍歷樹,根據記錄的深度找到最右值。
step 1:首先檢查兩個遍歷序列的大小,若是為0,則空樹不用打印。
step 2:建樹函數根據上述說,每次利用前序遍歷第一個元素就是根節點,在中序遍歷中找到它將二叉樹劃分為左右子樹,利用l1 r1 l2 r2分別記錄子樹部分在數組中分別對應的下標,並將子樹的數組部分送入函數進行遞歸。
step 3:dfs打印右視圖時,使用哈希表存儲每個深度對應的最右邊節點,初始化兩個棧輔助遍歷,第一個棧記錄dfs時的節點,第二個棧記錄遍歷到的深度,根節點先入棧。
step 4:對於每個訪問的節點,每次左子節點先進棧,右子節點再進棧,這樣訪問完一層後,因為棧的先進後出原理,每次都是右邊被優先訪問,因此我們在哈希表該層沒有元素時,添加第一個該層遇到的元素就是最右邊的節點。
step 5:使用一個變量逐層維護深度最大值,最後遍歷每個深度,從哈希表中讀出每個深度的最右邊節點加入數組中。
from collections import defaultdict
class Solution:
# 通過前序和中序,構建二叉樹
def buildTree(self, xianxu: List[int], l1: int, r1 :int, zhongxu: List[int], l2: int, r2:int):
if l1 > r1 or l2 > r2:
return None
# 構建節點
root = TreeNode(xianxu[l1])
# 用來保存根節點在中序遍歷列表的下標
rootIndex = 0
# 尋找根節點
for i in range(l2, r2+1):
if zhongxu[i] == xianxu[l1]:
rootIndex = i
break
# 左子樹的大小
leftsize = rootIndex - l2
# 右子樹的大小
rightsize = r2 - rootIndex
# 遞歸構建左子樹和右子樹,注意邊界值
root.left = self.buildTree(xianxu, l1+1, l1+leftsize, zhongxu, l2, l2+leftsize-1)
root.right = self.buildTree(xianxu, r1-rightsize+1, r1, zhongxu, rootIndex+1, r2)
return root
def rightSideView(self, root: TreeNode):
# 哈希表用於存儲每個深度對應的最右邊的節點
mp = defaultdict(int)
# 記錄最大深度
max_depth = -1
# 維護深度訪問節點、維護dfs時的深度
nodes, depths = [], []
nodes.append(root)
depths.append(0)
# 因為棧是先進後出,所以右邊的節點會被先處理
# 所以哈希表中記錄的一定是每一層的最右邊的節點
while nodes:
node = nodes.pop()
depth = depths.pop()
if node:
# 維護二叉樹的最大深度
max_depth = max([max_depth, depth])
# 如果不存在對應深度的節點,才會插入
if mp[depth] == 0:
mp[depth] = node.val
nodes.append(node.left)
nodes.append(node.right)
depths.append(depth+1)
depths.append(depth+1)
res = []
for i in range(max_depth+1):
res.append(mp[i])
return res
def solve(self , xianxu: List[int], zhongxu: List[int]) -> List[int]:
res = []
# 空節點
if len(xianxu) == 0:
return res
# 建立二叉樹
root = self.buildTree(xianxu, 0, len(xianxu)-1, zhongxu, 0, len(zhongxu)-1)
# 找每一層最右邊的節點
return self.rightSideView(root)
時間復雜度: O ( n 2 ) O(n^2) O(n2),建樹部分遞歸為O(n),中序遍歷中尋找根節點最壞O(n),dfs每個節點訪問一遍O(n),故為 O ( n 2 ) O(n^2) O(n2)。
空間復雜度: O ( n ) O(n) O(n),遞歸棧、哈希表、棧的空間都為O(n)。
對於方法一中每次要尋找中序遍歷中的根節點很浪費時間,我們可以利用一個哈希表直接將中序遍歷的元素與前序遍歷中的下標做一個映射,後續查找中序根節點便可以直接訪問了。 同時除了深度優先搜索可以找最右節點,我們也可以利用層次遍歷,借助隊列,找到每一層的最右。值得注意的是:每進入一層,隊列中的元素個數就是該層的節點數。 因為在上一層他們的父節點將它們加入隊列中的,父節點訪問完之後,剛好就是這一層的所有節點。
step 1:首先檢查兩個遍歷序列的大小,若是為0,則空樹不用打印。
step 2:遍歷前序遍歷序列,用哈希表將中序遍歷中的數值與前序遍歷的下標建立映射。
step 3:按照方法一遞歸劃分子樹,只是可以利用哈希表直接在中序遍歷中定位根節點的位置。
step 4:建立隊列輔助層次遍歷,根節點先進隊。
step 5:用一個size變量,每次進入一層的時候記錄當前隊列大小,等到size為0時,便到了最右邊,記錄下該節點元素。
from collections import defaultdict
import queue
class Solution:
dic = defaultdict(int)
# 通過前序和中序,構建二叉樹
def buildTree(self, xianxu: List[int], l1: int, r1 :int, zhongxu: List[int], l2: int, r2:int):
if l1 > r1 or l2 > r2:
return None
root = TreeNode(xianxu[l1])
# 用來保存根節點在中序遍歷列表的下標
rootIndex = self.dic[xianxu[l1]]
# 左子樹的大小
leftsize = rootIndex - l2
# 遞歸構建二叉樹
root.left = self.buildTree(xianxu, l1+1, l1+leftsize, zhongxu, l2, rootIndex-1)
root.right = self.buildTree(xianxu, l1+leftsize+1, r1, zhongxu, rootIndex+1, r2)
return root
def rightSideView(self, root: TreeNode):
res = []
q = queue.Queue()
q.put(root)
while not q.empty():
size = q.qsize()
while size:
size = size - 1
temp = q.get()
if temp.left:
q.put(temp.left)
if temp.right:
q.put(temp.right)
if size == 0:
res.append(temp.val)
return res
def solve(self , xianxu: List[int], zhongxu: List[int]) -> List[int]:
res = []
# 空節點
if len(xianxu) == 0:
return res
for i in range(len(zhongxu)):
self.dic[zhongxu[i]] = i
# 建立二叉樹
root = self.buildTree(xianxu, 0, len(xianxu)-1, zhongxu, 0, len(zhongxu)-1)
# 找每一層最右邊的節點
return self.rightSideView(root)
時間復雜度:O(n),其中 n 為二叉樹節點個數,每個節點訪問一次,哈希表直接訪問數組中的元素。
空間復雜度:O(n),遞歸棧深度、哈希表、隊列的空間都為O(n)。