We can also use the properties of binary search tree:For if one nodep與q都小於等於這個這個節點值,說明p、q都在這個節點的左子樹,而最近的公共祖先也一定在這個節點的左子樹;若是p與q都大於等於這個節點,說明p、q都在這個節點的右子樹,而最近的公共祖先也一定在這個節點的右子樹.而若是對於某個節點,p與q的值一個大於等於節點值,一個小於等於節點值,說明它們分布在該節點的兩邊,而這個節點就是最近的公共祖先,因此從上到下的其他祖先都將這個兩個節點放到同一子樹,只有最近公共祖先會將它們放入不同的子樹,每次進入一個子樹又回到剛剛的問題,因此可以使用遞歸.
step 1:首先檢查空節點,空樹沒有公共祖先.
step 2:對於某個節點,比較與p、q的大小,若p、q在該節點兩邊說明這就是最近公共祖先.
step 3:如果p、q都在該節點的左邊,則遞歸進入左子樹.
step 4:如果p、q都在該節點的右邊,則遞歸進入右子樹.
class Solution:
def lowestCommonAncestor(self , root: TreeNode, p: int, q: int) -> int:
if root is None:
return -1
if (p >= root.val and q <= root.val) or (p <= root.val and q >= root.val):
return root.val
elif p <= root.val and q <= root.val:
return self.lowestCommonAncestor(root.left, p, q)
else:
return self.lowestCommonAncestor(root.right, p, q)
時間復雜度:O(n),設二叉樹共有 n 個節點,The worst recursion traverse all the nodes.
空間復雜度:O(n),遞歸棧深度最壞為 n.
step 1:根據二叉搜索樹的性質,從根節點開始查找目標節點,當前節點比目標小則進入右子樹,當前節點比目標大則進入左子樹,直到找到目標節點.這個過程成用數組記錄遇到的元素.
step 2:分別在搜索二叉樹中找到p和q兩個點,並記錄各自的路徑為數組.
step 3:同時遍歷兩個數組,比較元素值,最後一個相等的元素就是最近的公共祖先.
class Solution:
def getPath(self, root: TreeNode, p: int):
path = []
while p != root.val:
path.append(root.val)
if p < root.val:
root = root.left
else:
root = root.right
path.append(root.val)
return path
def lowestCommonAncestor(self , root: TreeNode, p: int, q: int) -> int:
path1 = self.getPath(root, p)
path2 = self.getPath(root, q)
i = 0
# 最後一個相同的節點就是最近公共祖先
while i < len(path1) and i < len(path2):
if path1[i] == path2[i]:
res = path1[i]
i = i + 1
else:
break
return res
時間復雜度: O ( n ) O(n) O(n),設二叉樹共有 n 個節點,So the worst binary search tree into a list,Search to the target node need to O(n),Path to the front part of the same also need O(n).
空間復雜度: O ( n ) O(n) O(n),The longest recorded an array of the path is n.
既然要找到二叉樹中兩個節點的最近公共祖先,那我們可以考慮先找到兩個節點全部祖先,可以得到從根節點到目標節點的路徑,然後依次比較路徑得出誰是最近的祖先.找到兩個節點的所在可以深度優先搜索遍歷二叉樹所有節點進行查找.
step 1:利用dfs求得根節點到兩個目標節點的路徑:每次選擇二叉樹的一棵子樹往下找,同時路徑數組增加這個遍歷的節點值.
step 2:一旦遍歷到了葉子節點也沒有,則回溯到父節點,尋找其他路徑,回溯時要去掉數組中剛剛加入的元素.
step 3:然後遍歷兩條路徑數組,依次比較元素值.
step 4:找到兩條路徑第一個不相同的節點即是最近公共祖先
class Solution:
# Records are found too的路徑
flag = False
# 求根節點到目標節點的路徑,Different from the binary search tree
def dfs(self, root: TreeNode, path: List[int], o: int):
if root is None or self.flag:
return
path.append(root.val)
if root.val == o:
self.flag = True
return
# dfs遍歷查找
self.dfs(root.left, path, o)
self.dfs(root.right, path, o)
# 找到
if self.flag:
return
# 該子樹沒有,回溯
path.pop()
def lowestCommonAncestor(self , root: TreeNode, o1: int, o2: int) -> int:
path1 = []
path2 = []
# 求根節點到兩個節點的路徑
self.dfs(root, path1, o1)
# 重置flag,查找下一個
self.flag = False
self.dfs(root, path2, o2)
i = 0
# 最後一個相同的節點就是最近公共祖先
while i < len(path1) and i < len(path2):
if path1[i] == path2[i]:
res = path1[i]
i = i + 1
else:
break
return res
時間復雜度:O(n),其中 n 為二叉樹節點數,The recursive traversal binary tree each node求路徑,後續又遍歷路徑.
空間復雜度:O(n),最壞情況二叉樹化為鏈表,深度為 n,遞歸棧深度和路徑數組為 n.
step 1:如果o1和o2中的任一個和root匹配,那麼root就是最近公共祖先.
step 2:如果都不匹配,則分別遞歸左、右子樹.
step 3:如果有一個節點出現在左子樹,並且另一個節點出現在右子樹,則root就是最近公共祖先.
step 4:如果兩個節點都出現在左子樹,Is the lowest common ancestor in the left subtree,否則在右子樹.
step 5:繼續遞歸左、右子樹,直到遇到step1或者step3的情況.
class Solution:
def lowestCommonAncestor(self , root: TreeNode, o1: int, o2: int) -> int:
# 該子樹沒找到,返回-1
if root is None:
return -1
# 該節點是其中某一個節點
if o1 == root.val or o2 == root.val:
return root.val
# 左子樹尋找公共祖先
left = self.lowestCommonAncestor(root.left, o1, o2)
# 右子樹尋找公共祖先
right = self.lowestCommonAncestor(root.right, o1, o2)
# Left subtree is yet to find a,則在右子樹中
if left == -1:
return right
# 右子樹沒找到,則在左子樹中
if right == -1:
return left
# 否則是當前節點
return root.val
時間復雜度:O(n),其中 n 為節點數,The recursive traversal binary tree each node.
空間復雜度:O(n),最壞情況二叉樹化為鏈表,遞歸棧深度為 n.
Serialization of the binary tree node values out,放入一個字符串中,We can according to the sequence traversal thinking,遍歷二叉樹每個節點,And the node values stored in the string,我們用‘#’表示空節點,用‘!'Said between nodes and node split.
Deserialization is according to the given string,The binary tree reconstruction,Because the order of the string is a former sequence traversal,So when we rebuild the former sequence traversal,即可還原.
step 1:優先處理序列化,The first empty tree direct return“#”,然後調用SerializeFunctionBefore the function sequence recursively traversing binary tree.
SerializeFunction(root, res);
step 2:SerializeFunctionFunction is responsible for the former order recursive,根據“根左右”的訪問次序,優先訪問根節點,遇到空節點在字符串中添加 ‘#’,遇到非空節點,Add the corresponding node Numbers and ‘!’,Then, in turn, recursive into the left subtree is,右子樹.
# 根節點
str.append(root.val).append('!');
# 左子樹
SerializeFunction(root.left, str);
# 右子樹
SerializeFunction(root.right, str);
step 3:創建全局變量 index Said in a sequence of subscript(C++In the direct Pointers to complete).
step 4:Processing deserialization again,讀入字符串,If the string directly for “#”,就是空樹,否則還是調用DeserializeFunctionFunction before order recursive done.
TreeNode res = DeserializeFunction(str);
step 5:DeserializeFunctionFunction is responsible for the former order recursive build tree,遇到‘#’Is an empty node,Meet figures were based on the exclamation mark segmentation,Converts a string to a number to join the newly created node,依據 “根左右”,Creates the root node,Then, in turn, recursive into the left subtree is、Right subtree is to create a new node.
TreeNode root = new TreeNode(val);
......
# Deserialization and serialization consistent,Is before order
root.left = DeserializeFunction(str);
root.right = DeserializeFunction(str);

import sys
sys.setrecursionlimit(100000)
class Solution:
def __init__(self):
self.index = 0
self.s = ""
# 處理序列化
def SerializeFunction(self, root):
# 空節點
if not root:
self.s = self.s + '#'
return
# 根節點
self.s = self.s + str(root.val) + '-'
# 左子樹
self.SerializeFunction(root.left)
# 右子樹
self.SerializeFunction(root.right)
def Serialize(self, root):
if not root:
return '#'
self.s = ""
self.SerializeFunction(root)
return self.s
# Processing deserialization functions
def DeserializeFunction(self, s: str):
# When you arrive at leaf node,構建完畢,Returned to continue to build the parent node
# 空節點
if self.index >= len(s) or s[self.index] == '#':
self.index = self.index + 1
return None
# 數字轉換
val = 0
while s[self.index] != '-' and self.index != len(s):
val = val * 10 + int(s[self.index])
self.index = self.index + 1
root = TreeNode(val)
# Sequence exactly,構建完成
if self.index == len(s):
return root
else:
self.index = self.index + 1
root.left = self.DeserializeFunction(s)
root.right = self.DeserializeFunction(s)
return root
def Deserialize(self, s):
if s == '#':
return None
return self.DeserializeFunction(s)
時間復雜度:O(n),其中n為二叉樹節點數,前序遍歷,Each node traverse again.
空間復雜度:O(n),最壞情況下,二叉樹退化為鏈表,遞歸棧最大深度為n.
step 1:According to the first sequence traversal first points to establish the root node.
step 2:Then traverse sequence traversal found in the position of the root node in the array.
step 3:According to the number of nodes in the subtree will again two traversal sequence is divided into sub array,Will set up subtree subarray into function.
step 4:Until the subtree sequence length is 0,結束遞歸.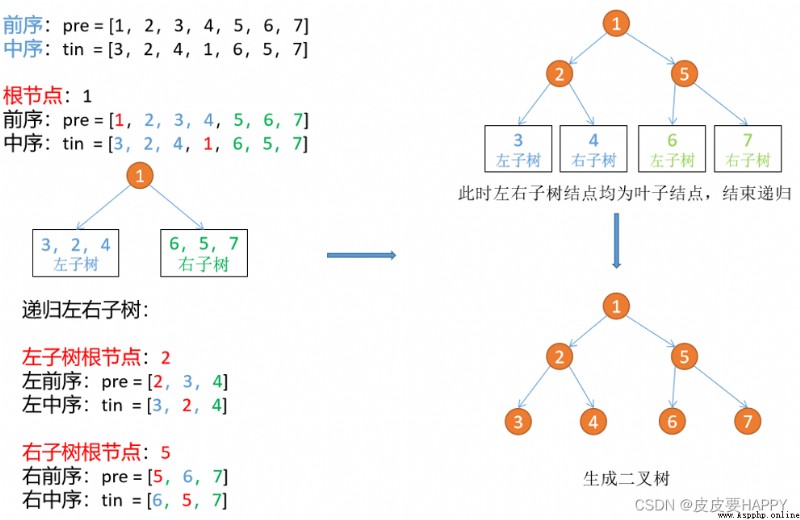
class Solution:
def reConstructBinaryTree(self , pre: List[int], vin: List[int]) -> TreeNode:
n = len(pre)
m = len(vin)
if n == 0 or m == 0:
return None
root = TreeNode(pre[0])
for i in range(len(vin)):
if pre[0] == vin[i]:
left_pre = pre[1:i+1]
left_vin = vin[:i]
root.left = self.reConstructBinaryTree(left_pre, left_vin)
right_pre = pre[i+1:]
right_vin = vin[i+1:]
root.right = self.reConstructBinaryTree(right_pre, right_vin)
break
return root
時間復雜度: O ( n ) O(n) O(n),其中 n 為數組長度,The number of nodes in the binary tree,Build each node into a recursive,Add up all the cycle in the recursive altogether n 次.
空間復雜度: O ( n ) O(n) O(n),遞歸棧最大深度不超過 n,輔助數組長度也不超過 n,Reconstruction of the binary tree space belongs to the necessary space,Do not belong to the auxiliary space.
With the aid of stack to solve the problem need to focus on one problem,就是前序遍歷挨著的兩個值比如m和n,They will have the following relations between the two kinds of circumstances.
1、n是m左子樹節點的值.
2、n是m右子樹節點的值或者是m某個祖先節點的右節點的值.
For the first case is easy to understand,如果m的左子樹不為空,那麼n就是m左子樹節點的值.
對於第二種情況,如果一個結點沒有左子樹只有右子樹,那麼n就是m右子樹節點的值,如果一個結點既沒有左子樹也沒有右子樹,那麼n就是m某個祖先節點的右節點,As long as find the ancestor nodes can.
step 1:Before the first sequence traversal the first number is still the root node,And set up the stack auxiliary traverse.
step 2:And then we began to judge,The preorder traversal of the adjacent two Numbers must be the only two things:Order before or after a is a left node before;Order before or after a previous right node or nodes whose ancestors right.
step 3:We can at the same time sequence traversalpre和vin兩個序列,To judge whether the left node,If is the left node keeps to the left deep,用棧記錄祖先,If it is not need to pop up the stack to the corresponding ancestors,然後進入右子樹,The whole process is similar to the recursive sequence traversal before.
class Solution:
def reConstructBinaryTree(self , pre: List[int], vin: List[int]) -> TreeNode:
n = len(pre)
m = len(vin)
if n == 0 or m == 0:
return None
s = []
root = TreeNode(pre[0])
cur = root
j = 0
for i in range(1,n):
# One is the first of a left child
if cur.val != vin[j]:
cur.left = TreeNode(pre[i])
s.append(cur)
cur = cur.left
# After a is a right before children,Or ancestors right child
else:
# 找到合適的cur,And then determine the right of his children
j = j + 1
# 彈出到符合的祖先
while s and s[-1].val == vin[j]:
cur = s.pop()
j = j + 1
# 給cur添加右節點
cur.right = TreeNode(pre[i])
cur = cur.right
return root
時間復雜度:O(n),其中 n 為數組長度,The number of nodes in the binary tree,遍歷一次數組,The cycle of pop-up stack up ton次.
空間復雜度:O(n),棧空間最大深度為 n,Reconstruction of the binary tree space belongs to the necessary space,Do not belong to the auxiliary space.
First of all done aspect,前序遍歷是根左右的順序,The order of the sequence traversal is left right in,Because the node values are the same,We can according to find the root node in the preorder traversal(Each subtree is part of the first is the),Again found in sequence traversal of the value of the corresponding,Separated from around the,On the left is the tree left subtree,The right is the right subtree of the tree,So will be divided to subproblems problem.
And print the right view that is find binary tree each layer of the rightmost node element,我們可以采取dfs(深度優先搜索)遍歷樹,Based on the depth of the records to find the right value.
step 1:首先檢查兩個遍歷序列的大小,若是為0,The empty tree don't print.
step 2:Done function according to the above said,Before each use sequence traversal first element is the root node,In the find it sequence traversal of the binary tree is divided into left and right subtrees,利用l1 r1 l2 r2Record the subtree part correspond in the array subscript,And the array part of the subtree into function recursive.
step 3:dfsPrint right view,Use the right side of the hash table to store each depth corresponding node,初始化兩個棧輔助遍歷,The first stack tracedfs時的節點,The second stack trace traverse to the depth of the,根節點先入棧.
step 4:For each access node,Each time the left child node advanced stack,The right child node into the stack again,After such access layer,Because of the stack after advanced a principle,Be priority access to the right every time,So we in the hash table the layer no elements,Add the first element is the most the right side of the layer meet node.
step 5:使用一個變量逐層維護深度最大值,Finally through each depth,Read from a hash table to join the right side of the depth of each node in the array.
from collections import defaultdict
class Solution:
# 通過前序和中序,構建二叉樹
def buildTree(self, xianxu: List[int], l1: int, r1 :int, zhongxu: List[int], l2: int, r2:int):
if l1 > r1 or l2 > r2:
return None
# 構建節點
root = TreeNode(xianxu[l1])
# Used to store the root node in the sequence the index to traverse the list
rootIndex = 0
# 尋找根節點
for i in range(l2, r2+1):
if zhongxu[i] == xianxu[l1]:
rootIndex = i
break
# 左子樹的大小
leftsize = rootIndex - l2
# 右子樹的大小
rightsize = r2 - rootIndex
# 遞歸構建左子樹和右子樹,注意邊界值
root.left = self.buildTree(xianxu, l1+1, l1+leftsize, zhongxu, l2, l2+leftsize-1)
root.right = self.buildTree(xianxu, r1-rightsize+1, r1, zhongxu, rootIndex+1, r2)
return root
def rightSideView(self, root: TreeNode):
# Hash table is used to store the right side of the depth of each corresponding node
mp = defaultdict(int)
# 記錄最大深度
max_depth = -1
# Depth of maintenance access node、維護dfs時的深度
nodes, depths = [], []
nodes.append(root)
depths.append(0)
# 因為棧是先進後出,So the right of the node will be first processed
# So in the hash table records must be the most the right side of each layer of the node
while nodes:
node = nodes.pop()
depth = depths.pop()
if node:
# 維護二叉樹的最大深度
max_depth = max([max_depth, depth])
# If there is no corresponding depth node,才會插入
if mp[depth] == 0:
mp[depth] = node.val
nodes.append(node.left)
nodes.append(node.right)
depths.append(depth+1)
depths.append(depth+1)
res = []
for i in range(max_depth+1):
res.append(mp[i])
return res
def solve(self , xianxu: List[int], zhongxu: List[int]) -> List[int]:
res = []
# 空節點
if len(xianxu) == 0:
return res
# 建立二叉樹
root = self.buildTree(xianxu, 0, len(xianxu)-1, zhongxu, 0, len(zhongxu)-1)
# To find the right each layer node
return self.rightSideView(root)
時間復雜度: O ( n 2 ) O(n^2) O(n2),Made part of the recursiveO(n),In the search for the root node in the sequence traversal the worstO(n),dfsEach node to access it againO(n),故為 O ( n 2 ) O(n^2) O(n2).
空間復雜度: O ( n ) O(n) O(n),遞歸棧、哈希表、棧的空間都為O(n).
In the sequence traversal method one time to look for the root node is a waste of time,We can use a hash table direct sequence traversal of the element and preorder traversal of the subscript to do a map,In the subsequent search sequence root node can have direct access to the. At the same time, in addition to the depth first search can find the right node,We can also use level traversal,借助隊列,Find the right of each layer.值得注意的是:每進入一層,Number of nodes in the queue is the number of elements in the this layer. Because in a layer of their parent node to join them in the queue,The parent node access after,Just this layer of all nodes.
step 1:首先檢查兩個遍歷序列的大小,若是為0,The empty tree don't print.
step 2:Traversal sequence traversal sequence before,用哈希表將中序遍歷中的數值與前序遍歷的下標建立映射.
step 3:According to the method of recursive cross molecular tree,Just can use hash table directly in sequence traversal in the positioning of the root node location.
step 4:建立隊列輔助層次遍歷,The root node advanced team.
step 5:用一個size變量,每次進入一層的時候記錄當前隊列大小,等到size為0時,Reach the most the right side,Record the node element.
from collections import defaultdict
import queue
class Solution:
dic = defaultdict(int)
# 通過前序和中序,構建二叉樹
def buildTree(self, xianxu: List[int], l1: int, r1 :int, zhongxu: List[int], l2: int, r2:int):
if l1 > r1 or l2 > r2:
return None
root = TreeNode(xianxu[l1])
# Used to store the root node in the sequence the index to traverse the list
rootIndex = self.dic[xianxu[l1]]
# 左子樹的大小
leftsize = rootIndex - l2
# 遞歸構建二叉樹
root.left = self.buildTree(xianxu, l1+1, l1+leftsize, zhongxu, l2, rootIndex-1)
root.right = self.buildTree(xianxu, l1+leftsize+1, r1, zhongxu, rootIndex+1, r2)
return root
def rightSideView(self, root: TreeNode):
res = []
q = queue.Queue()
q.put(root)
while not q.empty():
size = q.qsize()
while size:
size = size - 1
temp = q.get()
if temp.left:
q.put(temp.left)
if temp.right:
q.put(temp.right)
if size == 0:
res.append(temp.val)
return res
def solve(self , xianxu: List[int], zhongxu: List[int]) -> List[int]:
res = []
# 空節點
if len(xianxu) == 0:
return res
for i in range(len(zhongxu)):
self.dic[zhongxu[i]] = i
# 建立二叉樹
root = self.buildTree(xianxu, 0, len(xianxu)-1, zhongxu, 0, len(zhongxu)-1)
# To find the right each layer node
return self.rightSideView(root)
時間復雜度:O(n),其中 n 為二叉樹節點個數,每個節點訪問一次,哈希表直接訪問數組中的元素.
空間復雜度:O(n),遞歸棧深度、哈希表、隊列的空間都為O(n).