一、原理

1.定義

CRITIC方法是一種客觀權重賦權法。它的基本思路是確定指標的客觀權數以兩個基本概念為基礎。一是對比強度，它表示同一指標各個評價方案取值差距的大小，以標准差的形式來表現。二是評價指標之間的沖突性，指標之間的沖突性是以指標之間的相關性為基礎，如兩個指標之間具有較強的正相關，說明兩個指標沖突性較低。

2.作用

CRITIC權重法適用於判斷數據穩定性，並且適合分析指標或因素之間有著一定的關聯的數據。

二、相關概念

1.對比強度

是指同一個指標各個評價方案之間取值差距的大小，以標准差的形式來表現。標准差越大，說明波動越大，即各方案之間的取值差距越大，權重會越高。其中，假設m個待評對象，n個評價指標。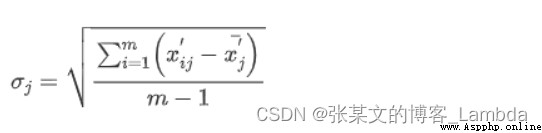

2.沖突性

指標之間的沖突性用相關系數進行表示，若兩個指標之間具有較強的正相關，說明其沖突性越小，權重會越低。

3.信息承載量

設信息承載量為Cj，公式為：

三、步驟

1.數據標准化

每個指標的數量級不一樣，需要把它們化到同一個范圍內比較。指標也都需要正向化。此篇把正向化和標准化結合。
設有m個待評對象，n個評價指標，可以構成數據矩陣X = (xij)mxn.

• 若xj為負向指標(越小越優型指標)，需如下處理：
  
• 若xj為正向指標(越大越優型指標)，需如下處理：
  

2.計算信息承載量

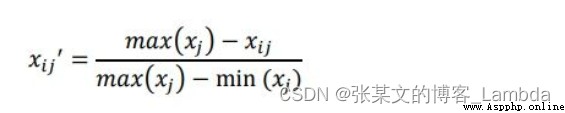
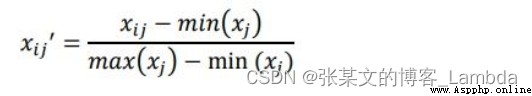
根據上述第二部分所列對比強度及沖突性公式，推導得信息承載量公式。
根據以上3個公式，計算所需信息承載量C。

3.計算權重

這裡將計算的信息承載量 Cj 進行歸一化，即為所計算的權重 W。可以看出，信息承載量越大時，權重越大。

4.計算評分

將權重 W 與處理後的矩陣 x 相乘，獲得測評對象的分數（該公式中，分數未轉為百分比形式）。

四、代碼

import numpy as np
''' 4 5 1 1 2 1 1 0.483 13.2682 0.0 4.3646 5.1070 0.4035 13.4909 39.0131 3.6151 5.5005 0.8979 25.7776 9.0513 4.8920 7.5342 0.5927 16.0245 13.2935 4.4529 6.5913 '''
'''1.輸入數據'''
print("請輸入參評對象數目：")
n = eval(input())
print("請輸入評價指標數目：")
m = eval(input())
print("請輸入指標類型：1:極大型，2：極小型")
kind = input().split(" ")
print("請輸入矩陣：")
X = np.zeros(shape=(n, m))
for i in range(n):
X[i] = input().split(" ")
X[i] = list(map(float, X[i]))
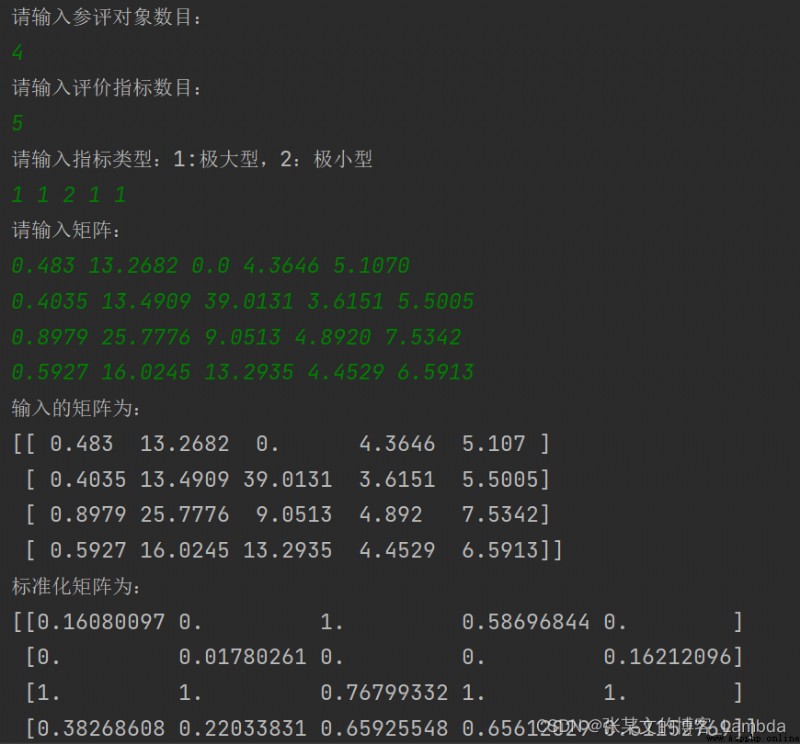
print("輸入的矩陣為：\n{}".format(X))
'''2.標准化處理'''
def maxTomax(maxx, minx, x):
x = list(x)
ans = [[(e-minx)]/(maxx-minx) for e in x]
return np.array(ans)
def minTomax(maxx, minx, x):
x = list(x)
ans = [[(maxx-e)]/(maxx-minx) for e in x]
return np.array(ans)
A = np.zeros(shape=(n, 1))
for i in range(m):
maxA = max(X[:, i])
minA = min(X[:, i])
if kind[i] == "1":
v = maxTomax(maxA, minA, X[:, i])
elif kind[i] == "2":
v = minTomax(maxA, minA, X[:, i])
if i == 0:
A = v.reshape(-1, 1)
else:
A = np.hstack([A, v.reshape(-1, 1)])
print("標准化矩陣為：\n{}".format(A))
'''3.計算對比強度'''
V = np.std(A, axis=0)
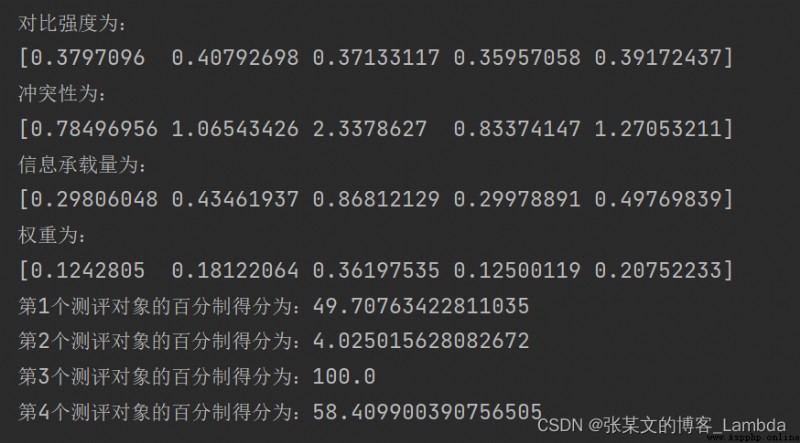
print("對比強度為：\n{}".format(V))
'''4.計算沖突性'''
A2 = list(map(list, zip(*A))) # 矩陣轉置
r = np.corrcoef(A2) # 求皮爾遜相關系數
f = np.sum(1-r, axis=1)
print("沖突性為：\n{}".format(f))
'''5.計算信息承載量'''
C = V*f
print('信息承載量為：\n{}'.format(C))
'''6.計算權重'''
w = C/np.sum(C)
print('權重為：\n{}'.format(w))
'''7.計算得分'''
s = np.dot(A, w)
Score = 100*s/max(s)
for i in range(len(Score)):
print(f"第{
i+1}個測評對象的百分制得分為：{
Score[i]}")

五、參考鏈接

1.CSDN博客筆記
2.知乎筆記