一、原理

1.定義

CRITIC方法是一種Objective weight empowerment法.Its basic idea is to determine the objective weights of indicators based on two basic concepts.一是Contrast strength,It represents the size of the difference between the values ​​of each evaluation scheme of the same indicator,以標准差的形式來表現.The second is between the evaluation indicators沖突性,The conflict between indicators is based on the correlation between indicators,For example, there is a strong positive correlation between the two indicators,It shows that the two indicators are less conflicting.

2.作用

CRITICThe weight method is suitable for judging data stability,And it is suitable for analyzing indicators or factorscertain connection的數據.

二、相關概念

1.Contrast strength

It refers to the size of the value gap between the evaluation schemes of the same indicator,以標准差的形式來表現.標准差越大,說明波動越大,即各方案之間的取值差距越大,權重會越高.其中,假設m個待評對象,n個評價指標.

2.沖突性

The conflict between the indicators is represented by the correlation coefficient,若兩個指標之間具有較強的正相關,說明其沖突性越小,權重會越低.

3.信息承載量

Let the information carrying capacity be Cj,公式為：

三、步驟

1.數據標准化

每個指標的數量級不一樣,需要把它們化到同一個范圍內比較.指標也都需要正向化.此篇把正向化和標准化結合.
設有m個待評對象,n個評價指標,可以構成數據矩陣X = (xij)mxn.

• 若xj為負向指標(越小越優型指標),需如下處理：
  
• 若xj為正向指標(越大越優型指標),需如下處理：
  

2.Calculate the information carrying capacity

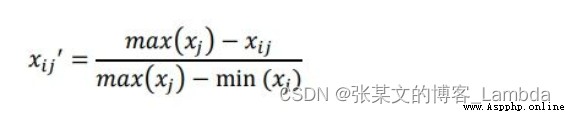
as listed in Part II aboveContrast strength及沖突性公式,推導得信息承載量公式.
根據以上3個公式,Calculate the required information carrying capacityC.

3.計算權重

The information carrying capacity will be calculated here Cj 進行歸一化,即為所計算的權重 W.可以看出,When the information carrying capacity is larger,權重越大.

4.計算評分

將權重 W 與處理後的矩陣 x 相乘,獲得測評對象的分數（該公式中,分數未轉為百分比形式）.

四、代碼

import numpy as np
''' 4 5 1 1 2 1 1 0.483 13.2682 0.0 4.3646 5.1070 0.4035 13.4909 39.0131 3.6151 5.5005 0.8979 25.7776 9.0513 4.8920 7.5342 0.5927 16.0245 13.2935 4.4529 6.5913 '''
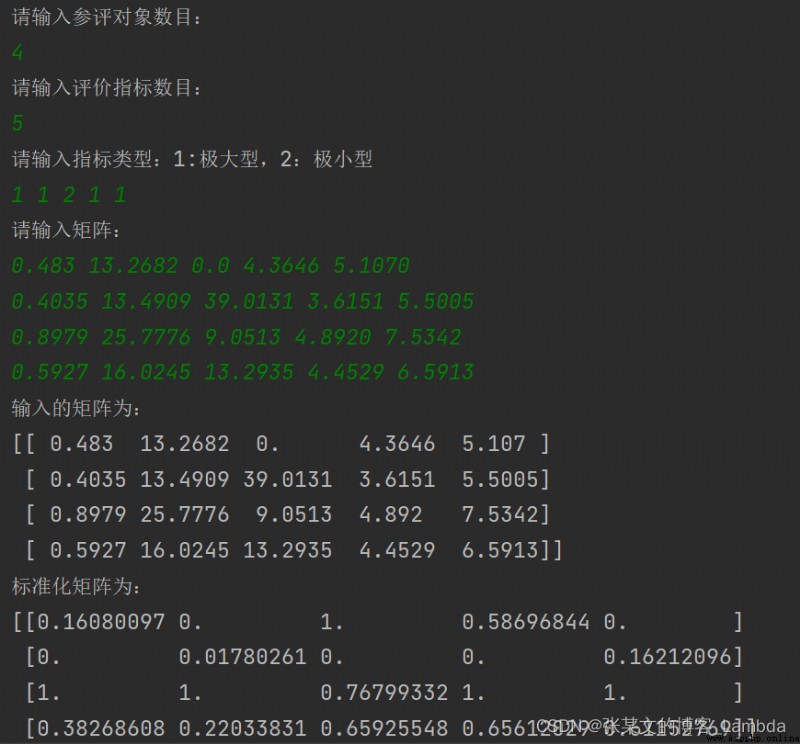
'''1.輸入數據'''
print("請輸入參評對象數目：")
n = eval(input())
print("請輸入評價指標數目：")
m = eval(input())
print("請輸入指標類型：1:極大型,2：極小型")
kind = input().split(" ")
print("請輸入矩陣：")
X = np.zeros(shape=(n, m))
for i in range(n):
X[i] = input().split(" ")
X[i] = list(map(float, X[i]))
print("輸入的矩陣為：\n{}".format(X))
'''2.標准化處理'''
def maxTomax(maxx, minx, x):
x = list(x)
ans = [[(e-minx)]/(maxx-minx) for e in x]
return np.array(ans)
def minTomax(maxx, minx, x):
x = list(x)
ans = [[(maxx-e)]/(maxx-minx) for e in x]
return np.array(ans)
A = np.zeros(shape=(n, 1))
for i in range(m):
maxA = max(X[:, i])
minA = min(X[:, i])
if kind[i] == "1":
v = maxTomax(maxA, minA, X[:, i])
elif kind[i] == "2":
v = minTomax(maxA, minA, X[:, i])
if i == 0:
A = v.reshape(-1, 1)
else:
A = np.hstack([A, v.reshape(-1, 1)])
print("標准化矩陣為：\n{}".format(A))
'''3.Calculate the contrast intensity'''
V = np.std(A, axis=0)
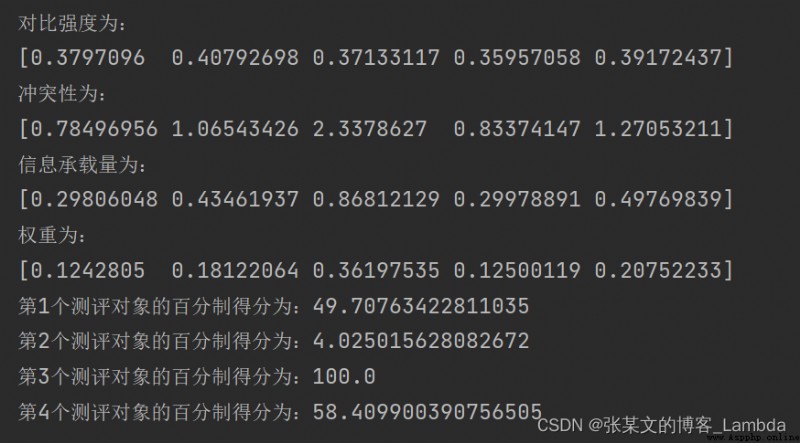
print("The contrast strength is ：\n{}".format(V))
'''4.Calculate conflict'''
A2 = list(map(list, zip(*A))) # 矩陣轉置
r = np.corrcoef(A2) # 求皮爾遜相關系數
f = np.sum(1-r, axis=1)
print("Conflict is：\n{}".format(f))
'''5.Calculate the information carrying capacity'''
C = V*f
print('The information carrying capacity is ：\n{}'.format(C))
'''6.計算權重'''
w = C/np.sum(C)
print('權重為：\n{}'.format(w))
'''7.計算得分'''
s = np.dot(A, w)
Score = 100*s/max(s)
for i in range(len(Score)):
print(f"第{
i+1}個測評對象的百分制得分為：{
Score[i]}")

五、參考鏈接

1.CSDN博客筆記
2.知乎筆記