本篇文章內容充實 文字量較大 每一個知識點都會附帶有模版題以供練習 並有詳細注釋
若能基本掌握 穩穩拿省一~~如遇我解釋不清楚的地方 歡迎私信我 我會耐心解答呀
目錄
動態規劃
01背包
完全背包
多重背包
01背包最大價值方案數
完全背包填滿背包的方案數
最長上升子序列
最長公共子串
最長公共子序列
最長公共上升子序列
最長上升子序列和
最長回文子串
最長回文子序列
二分
檢測是否最大滿足
檢測是否最小滿足
全排列
下一個全排列
N個字符/數字的全排列
N個字符選K個字符的組合
求組合數
快速冪
篩素數
唯一分解定理
最大公約數與最小公倍數
圖論
建圖方法
最短路 Dijkstra算法(沒有負邊權)
最短路 SPFA算法(有負邊權)
最小生成樹
拓撲排序
最近公共祖先
二分圖匹配
並查集
前綴和與差分
前綴和
差分
搜索
深度優先搜索
廣度優先搜索
記憶化搜索
樹狀數組
單調棧
寫在最後
N,V = map(int,input().split()) # 物品數量和背包容積
v = [] ; w = [] # 每個物品的體積和價值
for i in range(N) : # 讀入數據
a,b = map(int,input().split())
v.append(a) ; w.append(b)
dp = [0]*(V+1) # dp數組
for i in range(N) :
for j in range(V,v[i]-1,-1) :
dp[j] = max(dp[j],dp[j-v[i]]+w[i]) # 狀態轉移方程
print(dp[V])模版題鏈接: 2. 01背包問題 - AcWing題庫
n,m=map(int,input().split()) # 物品個數 背包容積
v=[0 for i in range(n+10)] # 物品體積
w=[0 for i in range(n+10)] # 物品價值
# 在前i個物品中選且背包體積為j時的最大價值
dp=[[0 for i in range(n+10)] for j in range(n+10)]
for i in range(1,n+1):
vv,ww=map(int,input().split())
v[i]=vv
w[i]=ww
for i in range(1,n+1) :
for j in range(m+1) :
dp[i][j] = dp[i-1][j]
if j >= v[i]:
dp[i][j] = max(dp[i][j],dp[i][j-v[i]]+w[i])
print(dp[n][m])模版題鏈接:3. 完全背包問題 - AcWing題庫
N,V = map(int,input().split()) # 物品個數 背包體積
w = [] ; v = [] ; num = [] # 每個物品的價值 體積 個數
for i in range(N) :
a,b,c = map(int,input().split())
num.append(c) ; v.append(a) ; w.append(b)
dp = [0 for i in range(V+1)] # 當背包體積為i時能裝下的最大價值
for i in range(N) :
for j in range(V,v[i]-1,-1) :
for k in range(num[i]+1) : # 枚舉一下這個物品能裝多少個
if k*v[i] > j : break # 大於背包體積則不能裝了
dp[j] = max(dp[j],dp[j-k*v[i]]+k*w[i])
print(dp[V])模版題鏈接: 4. 多重背包問題 I - AcWing題庫
n,V = map(int,input().split())
dp = [0 for j in range(V+1)] # 背包體積為j時能達到的最大價值
g = [1 for j in range(V+1)] # 背包體積為j時能達到最大價值的方案數
for i in range(1,n+1):
v,w = map(int,input().split())
for j in range(V,v-1,-1):
# 和01背包很像 只不過轉移到對象是方案數
if dp[j] == dp[j-v]+w : g[j] += g[j-v]
elif dp[j] < dp[j-v]+w : g[j] = g[j-v]
dp[j] = max(dp[j], dp[j-v]+w)
print(g[V])
模版題鏈接:11. 背包問題求方案數 - AcWing題庫
N = int(input())
dp = [0 for i in range(N+1)] #
dp[0] = 1
for i in range(1,N) :
for j in range(i,N+1) :
dp[j] += dp[j-i]
print(dp[N])模版題鏈接: 279. 自然數拆分 - AcWing題庫
num = int(input())
mountBox = list(map(int,input().split())) # 數組
Maxlen = [1 for i in range(num)] # 以第i個數字結尾的最長上升子序列
for i in range(num) :
for j in range(i) : # 枚舉比i靠前的數
if mountBox[j] < mountBox[i] : # 如果這個數比當前數小
Maxlen[i] = max(Maxlen[j]+1,Maxlen[i]) # 更新答案
print(max(Maxlen))模版題鏈接: [NOIP1999 普及組] 導彈攔截 - 洛谷
n = int(input())
list1 = list(map(int,input().split()))
list2 = list(map(int,input().split()))
# list1前i長的子串和list2前j長的子串的最長公共子串
Map = [[0 for i in range(len(list1)+1)]for j in range(len(list2)+1)]
for i in range(1,len(list2)+1) :
for j in range(1,len(list1)+1) :
if list2[i-1] == list1[j-1] : # 如果當前字符相同
Map[i][j] = Map[i-1][j-1] + 1 # 在原基礎上+1
else :
Map[i][j] = 0 # 否則為0
print(Map[-1][-1])模版題鏈接:3875. 最長公共子串 - AcWing題庫
n = int(input())
list1 = list(map(int,input().split()))
list2 = list(map(int,input().split()))
Map = [[0 for i in range(len(list1)+1)]for j in range(len(list2)+1)]
for i in range(1,len(list2)+1) :
for j in range(1,len(list1)+1) :
if list2[i-1] == list1[j-1] :
Map[i][j] = Map[i-1][j-1] + 1
else : # 所有代碼和最長公共子串一樣 只是這裡不同 注意!
Map[i][j] = max(Map[i-1][j],Map[i][j-1])
print(Map[-1][-1])模版題鏈接: 【模板】最長公共子序列 - 洛谷
請看這篇博客:Python:最長公共上升子序列模版_KS想去海底的博客-CSDN博客
模版題鏈接:272. 最長公共上升子序列 - AcWing題庫
請看這篇博客:Python:最長上升子序列和_KS想去海底的博客-CSDN博客
模版題鏈接:活動 - AcWing
s = input() # 讀入目標字符串
length = len(s)
dp = [[0 for i in range(length+10)]for j in range(length+10)]
#從第i個字符到第j個字符的最長回文串
res = ''
for l in range(1,length+1) : # 類似區間dp 枚舉子串長度
i = 0 #從第0個字符開始
while i + l - 1 < length : # 只要比總長短
j = i + l - 1 # 子串右端點
if l == 1 : # 長度為1的情況
dp[i][j] = 1
elif l == 2 : # 長度為2的情況
if s[i] == s[j] : dp[i][j] = 2
else : # 否則 如果當前左右端點字符相同
if s[i] == s[j] and dp[i+1][j-1] : dp[i][j] = dp[i+1][j-1] + 2
if dp[i][j] > len(res) : res = s[i:j+1]
i += 1
print(len(res))
模版題鏈接:1524. 最長回文子串 - AcWing題庫
s = input()
length = len(s)
dp = [[0 for i in range(length)]for j in range(length)] # dp[i][j]表示 第i個字符到第j個字符的最長回文子序列長度
for i in range(length) :
dp[i][i] = 1
for i in range(length-1,-1,-1) : # 可以想像為往兩端擴展
for j in range(i+1,length) :
if s[i] == s[j] : dp[i][j] = dp[i+1][j-1]+2
else : dp[i][j] = max(dp[i+1][j],dp[i][j-1])
print(dp[0][length-1])
模版題鏈接:3996. 塗色 - AcWing題庫
def check(x):
if(s[x]<=goal): return True
return False
s=[int(i) for i in input().split()]
goal=int(input())
left=0
right=len(s)-1# 左右端點
while(left<right):
mid=(left+right+1) // 2
if(check(mid)):
left=mid
else:
right=mid-1
print(left,s[left])
def check(x):
if(s[x]>=goal):
return True
return False
s=[int(i) for i in input().split()]
goal=int(input())
left=0
right=len(s)-1
while(left<right):
mid=(left+right)>>1
if(check(mid)):
right=mid
else:
left=mid+1
print(left,s[left])
模版題鏈接:113. 特殊排序 - AcWing題庫
# 對於12345的序列 最多讓我數到54321
def nextP(index):
global s
for t in range(index):
if(n<=1): # 如果一共的字母小於等於1 沒什麼要干的 返回
return
for i in range(n-2,-1,-1):
# 從後往前看 找到第一個不是降序的數x
if(s[i]<s[i+1]):
for j in range(n-1,-1,-1):
if(s[j]>s[i]): # 從後往前找 找到第一個大於x的數
s[i],s[j]=s[j],s[i] # 把它們交換
s[i+1:]=sorted(s[i+1:]) # 後面按照升序排序
break
break
else:
if(i==0): s.sort()
n=int(input())
index=int(input())
s=[int(i) for i in input().split()]
nextP(index)
print(' '.join(map(str,s)))
模版題鏈接:[NOIP2004 普及組] 火星人 - 洛谷
# n個數字的不同排列
from itertools import permutations
n=int(input())
s=[i for i in input().split()]
for p in permutations(s):
print("".join(map(str,p)))
# n個字母的不同排列
str=list(input().split()) # 根據空格劃分開
for p in permutations(str):
print("".join(p))
from itertools import combinations
n,k=map(int,input().split())
s=[i for i in range(1,n+1)]
for comb in combinations(s,k):
print("".join(map(str,comb)))
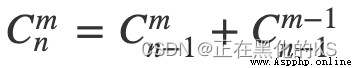
# 求組合數Cab
N=2010
mod=1e9+7
c=[[0 for i in range(N)] for j in range(N)]
def get():
global c
for i in range(N):
for j in range(i+1):
if(j==0): #
c[i][j]=1
else: # 用公式計算c[i][j]
c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod
n=int(input())
get()
for k in range(n):
a,b=map(int,input().split())
print(c[a][b])
小提示:Python語言其實可以不用背快速冪模版 因為自帶的pow函數速度已經比快速冪還快了
但需要理解原理 可能會遇到變種題!
def power(base,exponent): # base : 底數 / exponent : 指數
res = 1
while exponent:
if exponent & 1: # 判斷當前的最後一位是否為1,如果為1的話,就需要把之前的冪乘到結果中。
res *= base
base *= base # 一直累乘,如果最後一位不是1的話,就不用了把這個值乘到結果中,但是還是要乘。
exponent = exponent >> 1
return res
模版題鏈接:【模板】快速冪||取余運算 - 洛谷
這裡給出的是線性篩法 速度比樸素的篩法要快
# 線性篩質數
N=1000010
n=int(input())
cnt=0 # 用來計算有幾個素數
primes=[] # 用來存素數
def get_primes(n):
global cnt,primes
st=[False for i in range(N)] # 是否被篩過
for i in range(2,n+1):
if(st[i]==0): # 如果沒被篩過 是素數
primes.append(i) # 放到素數列表中
cnt+=1
for j in range(N):
if(primes[j]>n//i): break # 枚舉已經篩過的素數
st[primes[j]*i]=1 # 將他們標為已經篩過了
if(i%primes[j]==0): break
get_primes(n)
print(cnt)
模版題鏈接:【模板】線性篩素數 - 洛谷

import math
a,b = map(int,input().split())
t1 = math.gcd(a,b) # 最大公因數
t2 = print(a*b//math.gcd(a,b)) # 最小公倍數
模版題鏈接:3642. 最大公約數和最小公倍數 - AcWing題庫
# 鄰接表存圖 N個點 M條邊
N = int(input()) ; M = int(input())
Map = [dict() for i in range(N+1)]
for i in range(M) :
a,b,c = map(int,input().split()) # 起點 終點 權值
Map[a][b] = c
# 鄰接矩陣存圖
Map = [[0]*(N+1) for i in range(N+1)]
for i in range(M) :
a,b,c = map(int,input().split()) # 起點 終點 權值
Map[a][b] = c
# 推薦第一種 空間消耗相對少
import heapq
def dijkstra(G,start): ###dijkstra算法
INF = float('inf')
dis = dict((key,INF) for key in G) # start到每個點的距離
dis[start] = 0
vis = dict((key,False) for key in G) #是否訪問過,1位訪問過,0為未訪問
###堆優化
pq = [] #存放排序後的值
heapq.heappush(pq,[dis[start],start])
#path = dict((key,[start]) for key in G) #記錄到每個點的路徑
while len(pq)>0:
v_dis,v = heapq.heappop(pq) #未訪問點中距離最小的點和對應的距離
if vis[v] == True:
continue
vis[v] = True
#p = path[v].copy() #到v的最短路徑
for node in G[v]: #與v直接相連的點
new_dis = dis[v] + float(G[v][node])
if new_dis < dis[node] and (not vis[node]): #如果與v直接相連的node通過v到src的距離小於dis中對應的node的值,則用小的值替換
dis[node] = new_dis #更新點的距離
heapq.heappush(pq,[dis[node],node])
#temp = p.copy()
#temp.append(node) #更新node的路徑
#path[node] = temp #將新路徑賦值給temp
return dis,path
if __name__ == '__main__':
G = {1:{1:0, 2:10, 4:30, 5:100},
2:{2:0, 3:50},
3:{3:0, 5:10},
4:{3:20, 4:0, 5:60},
5:{5:0},
}
distance,path = dijkstra(G,1)
模版題鏈接:【模板】單源最短路徑(標准版) - 洛谷
def spfa(s) :
tot = 0
queue = collections.deque() # 雙端隊列的SFL優化
queue.append(s) # s是起點
dis = [INF for i in range(P+1)] # 起點到每個點的最近距離
dis[s] = 0 # 到起點自己是0
vis = [0 for i in range(P+1)] # 第i個點是否在隊列中
vis[s] = 1
while queue :
now = queue.popleft() # 第一個元素出隊
vis[now] = 0
for i in range(1,P+1) :
if Map[now][i] == INF : continue # 若不連通則跳過
if dis[i] > dis[now] + Map[now][i] :
dis[i] = dis[now] + Map[now][i]
if not vis[i] : # 若該點不在隊列中 放入隊列
vis[i] = 1
# SFL優化 如果當前點的dis小於隊頭元素的dis,則插入隊頭,反之隊尾
if len(queue) != 0 and dis[i] < dis[queue[0]] :
queue.appendleft(i)
else : queue.append(i)
for item in start :
if dis[item] > INF//2 : return INF # 如果這點不可達,直接返回無窮大
tot += dis[item]
return tot
模版題鏈接:1127. 香甜的黃油 - AcWing題庫
n,k = map(int,input().split()) # 點數 邊數
edges = [] # 存每一條邊
for i in range(k) :
a,b,c = map(int,input().split())
edges.append((a,b,c))
# 並查集模版
def root(x) :
if x != p[x] :
p[x] = root(p[x])
return p[x]
def union(a,b) :
p[root(a)] = root(b)
p = [i for i in range(n+1)] # 並查集列表
edges.sort(key = lambda x : x[2]) # 按照邊權從小到大排序
res = 0
while edges :
come,to,weight = edges.pop(0)
if root(come) != root(to) :
union(come,to) # 每次連接兩條邊
res += weight
print(weight)模版題鏈接:【模板】最小生成樹 - 洛谷
#准備工作上需要一個字典:用於存放連接關系
def topsort(graph):
#初始化所有點的入度為0
indegrees=dict((i,0) for i in graph.keys())
#傳入入度大小
for i in graph.keys():
for j in graph[i]:
indegrees[j]+=1#'a':'cd',代表a指向c和d,那麼c和d的入度增加1
#獲取入度為0的頂點
stack=[i for i in indegrees.keys() if indegrees[i]==0]
#創建拓撲序列
seq=[]
while stack:#深搜
tmp=stack.pop()#出棧
seq.append(tmp)#加入拓撲序列
for k in graph[tmp]:#遍歷鄰居,鄰居入度-1,鄰居入度為0入棧
indegrees[k]-=1
if indegrees[k]==0:
stack.append(k)
if len(seq)==len(graph):
print(seq)#輸出拓撲序列
else:
print('存在環')#當存在環,最終余下的點入度都不為0,Seq個數少於總頂點數
G={
'a':'cd',
'b':'df',
'c':'e',
'd':'efg',
'e':'g',
'f':'g',
'g':''
}
topsort(G)
#['b', 'a', 'd', 'f', 'c', 'e', 'g']模版題鏈接:164. 可達性統計 - AcWing題庫
import collections
from typing import List
class Solution:
# 樹中的節點都是int類型的
# bfs求解深度的一個好處是不容易爆棧而且是無向圖也不用標記是否已經被訪問了, 因為第一次訪問到的距離肯定是最短的
def bfs(self, root: int, fa: List[List[int]], depth: List[int], g: List[List[int]]):
q = collections.deque([root])
# 這裡0號點充當哨兵的作用
depth[0] = 0
depth[root] = 1
while q:
p = q.popleft()
for next in g[p]:
j = next
if depth[j] > depth[p] + 1:
depth[j] = depth[p] + 1
# 加入隊列
q.append(j)
# 預處理fa列表, k = 0是邊界為跳2 ^ 0 = 1步
fa[j][0] = p
# 因為節點個數最多為4 * 10 ** 4, 所以最多跳2 ^ 17, 這裡0號點作為哨兵的好處是可以當跳出根節點之後那麼節點的祖先是0, 可以避免邊界問題
for k in range(1, 17):
# 從當前節點跳2 ^ (k - 1)步到某一個節點然後從那個節點再往上跳2 ^ (k - 1)步那麼相當於是從j這個節點往上跳2 ^ j步
fa[j][k] = fa[fa[j][k - 1]][k - 1]
def lca(self, a: int, b: int, fa: List[List[int]], depth: List[int]):
# 確保a的深度比b的深度要大
if depth[a] < depth[b]:
a, b = b, a
# 1. 首先是從將深度較大的點跳到與深度較低的高度
for k in range(16, -1, -1):
if depth[fa[a][k]] >= depth[b]:
# a往上跳直到兩者的深度相等(兩個節點的深度一定會相等相當於是使用2 ^ i去湊來對應的深度是一定可以湊出來的)
a = fa[a][k]
# 說明b是a的祖先直接返回即可
if a == b: return a
# 2. 兩個節點同時往上跳直到fa[a][k] = fa[b][k], 說明a再往上跳一步就是當前的最近公共最先
for k in range(16, -1, -1):
if fa[a][k] != fa[b][k]:
a = fa[a][k]
b = fa[b][k]
# 節點a往上跳1步就是兩個節點的最近公共祖先
return fa[a][0]
# 需要理解其中的跳的過程
def process(self):
# n個節點
n = int(input())
root = 0
# 注意節點編號不一定是1~n
g = [list() for i in range(5 * 10 ** 4)]
for i in range(n):
a, b = map(int, input().split())
if b == -1:
# 當前的a是根節點
root = a
else:
# 注意是無向邊
g[a].append(b)
g[b].append(a)
INF = 10 ** 10
fa, depth = [[0] * 17 for i in range(5 * 10 ** 4)], [INF] * (5 * 10 ** 4)
# bfs預處理fa和depth列表
self.bfs(root, fa, depth, g)
# m個詢問
m = int(input())
for i in range(m):
x, y = map(int, input().split())
t = self.lca(x, y, fa, depth)
if t == x: print(1)
elif t == y: print(2)
else: print(0)
Solution().process()模版題鏈接: 【模板】最近公共祖先(LCA) - 洛谷
def find(x): # x表示左半部分第x號點
for j in graph[x]: # 遍歷與左半部分x號點相連的右半部分的節點
if st[j]==False:
st[j]=True
if match[j]==0 or find(match[j]): # 如果右半部分的第j號點沒有與左半部分匹配或者 與右半部分的第j號點匹配的左半部分的點可以匹配其他點
match[j] = x
return True
return False
模版題鏈接: 378. 騎士放置 - AcWing題庫
p = [i for i in range(N+1)]
def root(x) :
if x != p[x] : # 如果自己不是祖先
p[x] = root(p[x]) # 就尋找自己的父親是否是祖先
return p[x] # 返回祖先
def union(x,y) :
if root(x) != root(y) : # 如果兩個節點不是同一個祖先,說明該兩點之間沒有邊,if為假則說明有邊
p[root(x)] = root(y) # 就將兩個節點的祖先合並模版題鏈接: 【模板】並查集 - 洛谷
lst = list(map(int,input().split())) # 原數組
length = len(lst) # 原數組長度
lst = [0] + lst # 一般前綴和數組的第一個值都是0
for i in range(1,length+1) : # 處理成為前綴和數組
lst[i] += lst[i-1]模版題鏈接: 連續自然數和 - 洛谷
lst = list(map(int,input().split())) # 原數組
length = len(lst) # 原數組長度
for i in range(length-1,0,-1) : # 處理成為差分數組
lst[i] -= lst[i-1]模版題鏈接: 語文成績 - 洛谷
def dfs(u):
#當所有坑位被占滿 那麼輸出儲存的路徑
if u == n:
for i in range(0,n):
print(path[i], end = " ")
print('')
#另一種(幾乎)等價寫法ans.append(' '.join(list(map(str, path))))
#從1到n遍歷尋找第u個位置可以填的數
for i in range(1, n+1):
#確認數字狀態,是否已經被使用 如果沒有被占執行下面操作
if not state[i]: #等價於state[i]是[False]
path[u] = i #在坑位上填上次數字
state[i] = True #標注數字狀態,已經被使用
dfs(u+1) #進入下一層
state[i] = False #回溯恢復數字狀態
模版題鏈接:165. 小貓爬山 - AcWing題庫
"""
1. 初始化隊列
2. while queue不為空
3. 隊頂元素出隊
4. 遍歷,滿足條件的入隊
"""
def bfs():
queue = [1]
st[1] = True
d[1] = 0
while queue:
t = queue.pop(0)
if t not in graph: continue
for i in graph[t]:
if not st[i]:
st[i] = True
queue.append(i)
if d[i]==-1:
d[i] = d[t]+1
print(d[n])
模版題鏈接:188. 武士風度的牛 - AcWing題庫
關於記憶化搜索 我的這兩篇博客有詳細的講解:
藍橋杯/洛谷 : 最長滑雪道/滑雪 + 擴展題目(記憶化搜索 Python)_正在黑化的KS的博客-CSDN博客
Acwing:食物鏈(記憶化搜索 Python)_正在黑化的KS的博客-CSDN博客
def createTree(array) :
_array = [0] + array
length = len(array)
for i in range(1,length+1) :
j = i + (i & -i)
if j < length + 1 :
_array[j] += _array[i]
return _array
def lowbit(x) :
return x & (-x)
def update(array,idx,val) :
# prev = query(idx,idx+1,array) # 若將某節點值更新為val 則打開 / 若增加val 則關閉
idx += 1
# val -= prev
while idx < len(array) :
array[idx] += val
idx += lowbit(idx)
return array
def query(begin,end,array) : # 輸入索引皆以0為初始點
return _query(end,array) - _query(begin,array)
def _query(idx,array) :
res = 0
while idx > 0 :
res += array[idx]
idx -= lowbit(idx)
return res模版題鏈接:【模板】樹狀數組 1 - 洛谷
# 單調遞增
def IncreasingStack(nums):
stack = []
for num in nums:
# 當前值大於棧頂元素,將棧頂元素彈出
while stack and num >= stack[-1]:
stack.pop()
stack.append(num)
# 單調遞減
def DecreasingStack(nums):
stack = []
for num in nums :
while stack and num <= stack[-1]:
stack.pop()
stack.append(num)模版題鏈接:600. 仰視奶牛 - AcWing題庫
上述整理內容基本上是藍橋杯省賽的高頻考察內容 但並不是全部 當然正如我開頭說的
只要將這些內容理解並掌握 省一真的就是灑灑水啦~
如果覺得有用的話~給個贊好嗎 你的鼓勵就是我寫作的動力!