您现在的位置：程式師世界 >> 編程語言 > >> 更多編程語言 >> Python

同態加密：CKKS方案詳解及一個python實現:TenSEAL（不定期更新）

編輯：Python

部分資料來自於HEAAN作者的個人主頁：https://yongsoosong.github.io/files/slides/intro_to_CKKS.pdf

0x00 引流

本文是CKKS方案的簡介，在文章中不會涉及太多的數學。BGV方案和此方案大體類似。涉及CKKS更深層次的原理，請參考本專欄的其他博客。

0x01 同態加密的CKKS方案簡介

CKKS是2017年提出的同態加密方案。它支持浮點向量在密文空間的加減乘運算並保持同態，但是只支持有限次乘法的運算。

同態加密極簡介紹

舉個例子：
實數域裡有加法和乘法。多項式域裡面有多項式加法和多項式乘法。我們把實數域中的數或者向量映射到多項式域（加密），在多項式域裡做一些多項式加法和多項式乘法的運算之後，再把多項式映射回實數域（解密），得到的結果和實數域裡做對應的加法和乘法的結果相同或者相似。這種在私密領域（例如多項式域）做確保結果一致性的計算技術就叫同態加密。

LWE問題的極簡介紹

格(lattice)

在線性空間中給定一組線性無關的向量，其整數線性組合生成的集合稱為格。

關於格的詳細介紹，不妨移步這裡。

LWE問題
我們有了若干的 ( a , b ) (a, b) (a,b)對，其中 a a a為整數向量， b b b為整數。現在需要找一個線性函數 f f f，使得 f ( a ) ≈ b f(a) \approx b f(a)≈b。由Risez表示定理，總是存在一個和a形狀相同的 s s s，使得 f ( a ) = ( a , s ) f(a) = (a, s) f(a)=(a,s)，其中 ( a , s ) (a, s) (a,s)是 a a a和 s s s的內積。在CKKS中，這裡的線性函數就是 a a a和私鑰 s s s做內積，私鑰 s s s也是整數向量，即可以理解為求解線性方程組：
( a i , s ) = b i (a_i, s) = b_i (ai,s)=bi
但是，在LWE(learning with error)問題中，我們加入了一些誤差，此即：
( a i , s ) + e i = b i (a_i, s) + e_i = b_i (ai,s)+ei=bi
其中，內積 ( ∗ , s ) ( * ,s) (∗,s)就表示待定的 f ( ∗ ) f(*) f(∗)（因為f是線性的）。 e e e為整數，是引入的誤差。

如果沒有誤差的話，高斯消去法可以把 s s s解出來，但是誤差的引入和對 s s s中元素整數性的要求就使得解會特別病態甚至搞不出來符合要求的解。

上面所說的LWE問題是search-LWE問題，即已知 a , b a, b a,b尋找 s s s。
還有一種Decision-LWE問題，說的是判斷 b b b到底是隨機生成的整數還是由 ( a , s ) + e (a, s) + e (a,s)+e生成的東西。

RLWE問題
和LWE問題類似，只不過這裡的 a , b , s a, b, s a,b,s 都是整數多項式，而且對應地LWE裡的內積換成了多項式的乘法。可以證明，這個問題的求解也是困難的。

CKKS操作步驟

這裡就直接貼圖了，會附上一些文字說明幫助理解。

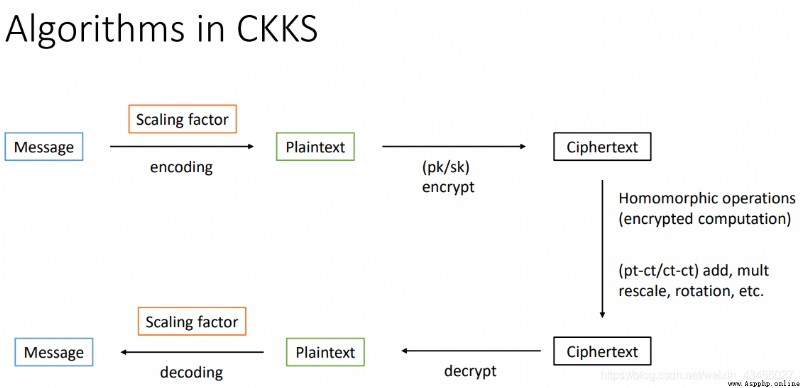
上圖是CKKS的一個大概流程。先對消息（向量）進行編碼，然後再加密，在密文空間進行一些運算後再解密，最後解碼成運算後的消息（向量）。
注意，這裡的編碼指的是將復數向量映射成為多項式，是為了方便下面進一步的加密，

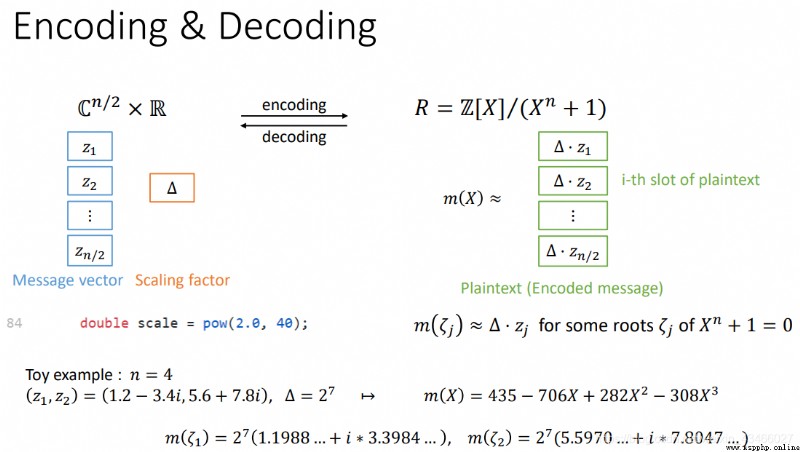
上圖是編解碼的方法。

一些數論背景

首先，給出一些記號。 Z M \mathbb Z_M ZM 是模 M M M剩余類， Z M ∗ \mathbb Z_M^* ZM∗ 是 Z M \mathbb Z_M ZM 裡所有帶有乘法逆的元素組成的集合。

ϕ ( n ) = # { k : g c d ( n , k ) = 1 } \phi(n) = \#\{k: gcd(n, k) = 1\} ϕ(n)=#{ k:gcd(n,k)=1} 是歐拉函數，其值為所有小於 n n n 且和 n n n 互素的正數的計數數目。

一個例子是 M = 8 M = 8 M=8， ϕ ( M ) = 4 \phi(M) = 4 ϕ(M)=4，因為可以考慮集合 { 1 , 3 , 5 , 7 } \{1, 3, 5, 7\} { 1,3,5,7}。

考慮 ω : = e 2 π i / m ∈ C \omega := e^{2\pi i/m} \in \mathbb C ω:=e2πi/m∈C 為原根， Φ M ( X ) : = ∏ j ∈ Z M ∗ ( X − ω j ) ∈ C [ X ] \Phi_M(X) := \prod_{j \in \mathbb Z_M^*}(X - \omega^j) \in \mathbb C[X] ΦM(X):=∏j∈ZM∗(X−ωj)∈C[X] 稱為 m m m 次分圓多項式。

編碼：Message -> m(X)

下面涉及的是將一個向量寫成多項式的形式。

對於 M > 4 M > 4 M>4，我們有 N = ϕ ( M ) = M / 2 N = \phi(M) = M/2 N=ϕ(M)=M/2 並且分圓多項式 Φ M ( X ) = X N + 1 \Phi_M(X) = X^N + 1 ΦM(X)=XN+1。為什麼要用

有下面的兩個性質：

M e s s a g e Message Message是一個 n 2 \frac{n}{2} 2n 維的復向量。在拿到一個復向量 M e s s a g e ∈ C n 2 Message \in C^{\frac{n}{2}} Message∈C2n之後，對它取一下共轭並且將原向量和共轭拼接在一起，得到増廣的 M e s s a g e ′ ∈ C n Message' \in C^n Message′∈Cn。

比如，我們拿到了一個復向量 ( 1 + 4 i , 5 − 2 i ) (1 + 4i, 5 - 2i) (1+4i,5−2i)。按照上面所說的做法，我們將它増廣為：

( 1 + 4 i , 5 − 2 i , 5 + 2 i , 1 − 4 i ) (1 + 4i, 5 - 2i, 5+2i, 1-4i) (1+4i,5−2i,5+2i,1−4i)

考慮復數域內多項式 X n + 1 X^n+1 Xn+1，它有 n n n個復根 ξ i \xi_i ξi，記這些復根組成的向量為 ξ \xi ξ ，並且前 n 2 \frac{n}{2} 2n個根和後 n 2 \frac{n}{2} 2n個根也是共轭的。

下面，我們求一個整數系數的插值多項式 m ( X ) m(X) m(X)（用牛頓插值、拉格朗日插值、快速傅裡葉變換啥的都可以），使得 m ( ξ ) ≈ Δ × M e s s a g e i ′ m(\xi) \approx \Delta \times Message'_i m(ξ)≈Δ×Messagei′。即把 X n + 1 = 0 X^n + 1 = 0 Xn+1=0 的復數根作為自變量丟到 m m m 裡面去，使得輸出的值是 M e s s a g e ′ Message' Message′的對應分量。

由於共轭性質，插值出來的 m m m 的系數都是實數。但是，CKKS最後要對整數進行操作，因此需要對多項式系數進行取整。如果直接對 m m m 系數取整，誤差會比較大。因此在這裡我們引入放大因子 Δ \Delta Δ ，將Message的數值放大，得到 m = m ⋅ Δ m = m · \Delta m=m⋅Δ之後再進行取整。這樣的話，可以盡可能保留小數的位數，提高加密的精度。但是引入了放大這樣一個操作之後，多項式系數就不可避免地變大了很多。如果再做很多乘法，那就不可避免地會出現溢出的情形。它的應對方法可以參考下面的重縮放部分。

m m m 即為對消息編碼的結果。

對編碼結果做存儲時，我們只需要存儲 m m m 的系數即可。

按理說，這裡的n需要是2的冪，但是由於這裡我們只涉及編碼解碼操作，所以沒有特別地提及這個事情，因為這裡n/2只要是整數的話，不影響後面加解密的運算。只有在旋轉和bootstrap下需要使用到n是2的冪這個條件，因為此時的分圓多項式的形狀比較好，是 X n + 1 X^n+1 Xn+1的形式。

解碼：Message <- m(X)

把上述步驟倒過來就行了。我們已知了 m m m，接下來把 ξ \xi ξ 帶進去就完事了。

最後別忘了除以 Δ \Delta Δ就行。

加密：m(X) -> (c0(X), c1(X))

這裡，我們取私鑰 ( 1 , s ) (1, s) (1,s)，公鑰 ( b = − a ⋅ s + e , a ) (b = -a·s + e, a) (b=−a⋅s+e,a)，其中 s s s 和 a a a 是向量， e e e是一個隨機數， b b b 是一個數。（這裡就由RLWE問題確保了一件事：僅使用公鑰的話很難解出私鑰）
則密文 ( c 0 , c 1 ) = r ( b , a ) + ( m + e 1 , e 2 ) = ( r b + m + e 1 , r a + e 2 ) (c_0, c_1) = r(b, a) + (m + e_1, e_2) = (rb + m + e_1, ra + e_2) (c0,c1)=r(b,a)+(m+e1,e2)=(rb+m+e1,ra+e2)，其中 r r r是隨機整數， e 1 , e 2 e_1, e_2 e1,e2是隨機的多項式（也可以理解為向量）。

涉及的所有乘法都相當於多項式乘法。

解密：m(X) <- (c0(X), c1(X))

計算 c 0 + c 1 s c_0 + c_1s c0+c1s即可，其結果約等於 m m m。

過程如下（這個式子最後的符號好像有點問題，我沒有改，可以結合評論區看一看，感謝評論區老哥指正）：
c 0 + c 1 s = r b + m + e 1 + r a ⋅ s + e 2 s = m + e 1 + e 2 s − e r c_0 + c_1s = rb + m + e_1 + ra·s + e_2s = m + e_1 + e_2s - er c0+c1s=rb+m+e1+ra⋅s+e2s=m+e1+e2s−er

加法（明文向量按元素相加）

兩個密文向量直接對應相加。

明文乘密文（明文多項式和密文多項式的乘法）
其本質就是 m × ( c 1 + c 2 s ) = m c 1 + m c 2 s m \times (c_1+ c_2s) = mc_1 + mc_2s m×(c1+c2s)=mc1+mc2s
直接把明文 m m m和密文中的 c 1 , c 2 c_1, c_2 c1,c2逐個做多項式乘法，得到的 ( c 1 m , c 2 m ) (c_1m, c_2m) (c1m,c2m)就是新的密文。但是，這裡的乘法會不可避免地導致乘積多項式的次數增加，進而需要更多的空間來存儲。這裡就需要用下文所說的重線性化來將乘積多項式控制到合適的多項式次數上。

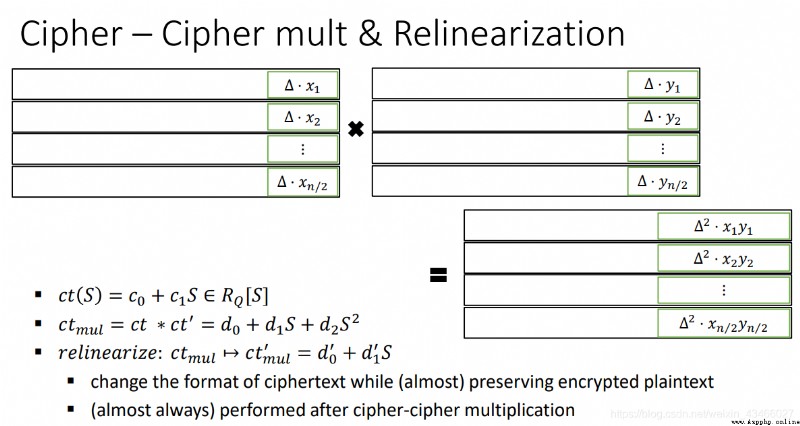
密文乘密文（密文多項式的乘法）
其本質就是 ( c 11 + c 12 s ) × ( c 21 + c 22 s ) = c 11 c 21 + ( c 21 c 12 + c 11 c 22 ) s + c 12 c 22 s 2 (c_{11}+ c_{12}s) \times (c_{21}+ c_{22}s) = c_{11}c_{21} + (c_{21}c_{12}+c_{11}c_{22})s + c_{12}c_{22}s^2 (c11+c12s)×(c21+c22s)=c11c21+(c21c12+c11c22)s+c12c22s2

重線性化
我們需要注意，明文和密文向量本質上是一個多項式，向量的內容是多項式的系數。多項式相乘完畢之後，其次數必然會升高。

比如，現在有兩個密文分別是 c 0 + c 1 s c_0 + c_1s c0+c1s和 c 2 + c 3 s c_2 + c_3s c2+c3s，如果直接做多項式相乘的話，得到的結果是 c 0 c 2 + ( c 0 c 3 + c 1 c 2 ) s + c 1 c 3 s 2 c_0c_2 + (c_0c_3 + c_1c_2)s + c_1c_3s^2 c0c2+(c0c3+c1c2)s+c1c3s2。

因此，密文空間的乘法會導致密文向量對應的密文多項式“次數”變大（但是如果把它對應的多項式進行解碼，忽略誤差的話，得到的Message還是同一個Message）。但是，從明文空間上看，上述動作還只是兩個向量的逐元素相乘，我們希望進行在密文空間中做乘法之後密文向量對應的多項式“次數”保持不變，即 ( c 0 + c 1 s ) ∗ ( c 2 + c 3 s ) = ( d 0 + d 1 s ) (c_0 +c_1s) * (c_2 + c_3s) = (d_0 + d_1s) (c0+c1s)∗(c2+c3s)=(d0+d1s)，沒有 s s s 的平方項。

解決方法是這樣的：我們啟用一個重線性化秘鑰 e v k = ( b ′ , a ′ ) = ( − a ′ ⋅ s + e ′ + b s 2 , a ′ ) evk = (b', a') = (-a'·s + e' + bs^2, a') evk=(b′,a′)=(−a′⋅s+e′+bs2,a′)。我們將示例 c 0 c 2 + ( c 0 c 3 + c 1 c 2 ) s + c 1 c 3 s 2 c_0c_2 + (c_0c_3 + c_1c_2)s + c_1c_3s^2 c0c2+(c0c3+c1c2)s+c1c3s2記為：

d 0 + d 1 s + d 2 s 2 d_0 + d_1s + d_2 s^2 d0+d1s+d2s2

其中 d 0 , d 1 , d 2 d_0, d_1, d_2 d0,d1,d2 都是可以用密文乘積計算出來的。

輸出的密文結果就是 ( c 1 ′ , c 2 ′ ) = ( d 0 , d 1 ) + P − 1 ⋅ d 2 ⋅ e v k (c'_1, c'_2) = (d_0, d_1) + P^{-1}·d_2·evk (c1′,c2′)=(d0,d1)+P−1⋅d2⋅evk，其中 P P P 是一個用於重縮放的特殊模數。

理由如下：

P − 1 d 2 ( b ′ , a ′ ) ⋅ ( 1 , s ) = P − 1 ⋅ d 2 ⋅ b ′ + P − 1 ⋅ d 2 ⋅ a ′ ⋅ s = d 2 s 2 + P − 1 d 2 e ′ ≈ d 2 s 2 P^{-1}d_2(b', a')·(1, s) = P^{-1}·d_2·b' + P^{-1}·d_2·a' ·s = d_2s^2 + P^{-1}d_2e' \approx d_2s^2 P−1d2(b′,a′)⋅(1,s)=P−1⋅d2⋅b′+P−1⋅d2⋅a′⋅s=d2s2+P−1d2e′≈d2s2

重縮放

上述推演過程中還是有不嚴謹地方的。其中一個重要的地方便是取模。

常理來說，我們對上面每一步運算都需要取模的，只是正常計算的過程中，我們算的數（包括編碼、加密、加法、乘法）都比較小，即使是放大因子 Δ \Delta Δ也比取模的模數小很多，所以取模一般是取個寂寞。因此我在上面就沒寫這個事兒。

但是當我們做乘法做多了之後，放大因子就多起來了，並且在最壞情況下放大因子數將呈指數增長。結果就有可能溢出模數了，溢出之後就白算了。

PS：放大因子增多的情況只出現於密文相乘的情形中。

CKKS的解決辦法是使用分層乘法機制。為此，CKKS設計了一個有限乘法全同態加密的機制，並且引入了一個模數鏈 Q = q 0 ⋅ p L Q = q_0 · p^L Q=q0⋅pL。這裡的 p p p 是和 Δ \Delta Δ “差不多”大小的素數， L L L 稱為乘法深度，可以理解為最多能做多少次乘法。剛加密的密文的模數是 Q Q Q，以後每做一次密文相乘， Δ \Delta Δ 都會變多，這裡就可以對系數除以一個 p p p（也相當於對模數除以 p p p ）來抵消掉這個增加的 Δ \Delta Δ，這樣就可以確保密文數據中自始至終僅有一個 Δ \Delta Δ，但是相應地會導致乘法深度的降低（因為做乘法會導致模數變小，因為對模數除以了 p p p，當模數變小到一定程度就可能溢出）。

旋轉(Rotation)

這個操作在SEAL庫中實現，但是在TenSEAL庫中似乎沒有實現。tenseal庫的作者表示，他們把旋轉操作集成到了乘法裡面，沒有直接提供旋轉操作的api。

它會用到一個Galois秘鑰，干的事情如下：

[1,2,3,4,5,0,0,0] -> [0,0,1,2,3,4,5,0] -> [4,5,0,0,0,1,2,3]

這裡應該是要用到Galois理論相關的東西。我近世代數課到這一塊老師講得太快了所以劃水過去的…過幾天學一學再補吧…

基本原理似乎是這樣（以明文為例）：明文是一個關於x的多項式，實現旋轉的話，需要將x替換成x的冪，然後再把結果模掉 X N + 1 X^N+1 XN+1。

20220415更，一個嚴謹的寫法在我的這篇博客裡有所涉及。

下面這張圖給出了一個例子供參考：

Bootstrapping

假如我們有一個即將耗盡乘法深度的密文，我們可以用Bootstrapping來讓它重新“煥發生機”，將它的乘法深度恢復到原始密文的深度。

這個事情的計算開銷比較大。目前有一些庫支持Bootstrapping操作，還有一些快速的bootstrapping方法。但是目前SEAL和TenSEAL庫都不支持Bootstrapping操作。

當然了，如果像我一樣懶得搞這些花裡胡哨的玩應的話，不妨直接把需要做bootstrap的向量發送給私鑰持有方，讓它給你解密後再加密就完事了。

20220727更，我簡單地寫了一下bootstrapping的原理和CKKS實現，歡迎來自各位dalao的寶貴意見。

雜項

矩陣的乘法是可以實現的。可以參見ICLR2021中TenSEAL庫的文章。還有很多專門研究如何在同態加密下做矩陣乘法的文章。

後來，我沒有直接用同態加密做矩陣的乘法，更多用到了矩陣乘向量，而且TenSEAL中對於矩陣的實現十分復雜，並且開銷比較大，所以這裡暫時放上一個比較簡單的矩陣乘向量的實現。

0x02 API

從一篇CKKS的應用論文中截取下來的東西，供大家參考：

0x03 同態加密庫PySyft和TenSEAL

網上常見的同態加密庫是SEAL庫，但是是用C++編寫的。

（還有一些正在用的過一陣子再補）

在把玩SEAL庫的過程中，本人倒在了第一步：編譯。

遂尋找替代品。

找到一個TenSEAL，它將SEAL用python進行包裝，編程比較方便。這個庫已經發表在了ICLR2021上。

也找到了一些FHE（全同態加密）的一些實現。

PySyft似乎包含了TenSEAL，留待日後品鑒。

（2021年7月23日更新，確實包含了TenSEAL，在 syft.frameworks.tenseal 中）
（我鴿了，因為暫時用不到PySyft）

（後來安了個ubuntu就發現各種同態加密庫都可以把玩，編譯也不再是啥大問題，遂休了TenSEAL。但是不得不說，TenSEAL庫對於新手是十分友好的）

熟悉TenSEAL

TenSEAL是一個具有Python接口的C++庫。

這個庫有兩個好處。

一個是安裝比SEAL省心，直接 pip install tenseal 完事了。

一個是不需要過多地考慮CKKS的實現細節（比如矩陣乘法的底層細節），直接梭哈就完事了。

TenSEALContext

這是本人對TenSEAL的一些API做的一個封裝。

這個Context上下文相當於對CKKS的秘鑰等參數做了一個封裝。我們只需要在編碼、加密、加、乘、解密的時候把上下文作為參數扔進去就完事了。

import tenseal as ts
import numpy as np
def gencontext():
context = ts.context(ts.SCHEME_TYPE.CKKS, 8192, coeff_mod_bit_sizes=[22 ,21, 21, 21, 21, 21, 21, 21, 21, 21])
context.global_scale = pow(2, 21)
context.generate_galois_keys()
return context
def encrypt(context, np_tensor):
return ts.ckks_tensor(context, np_tensor)
def decrypt(enc_tensor):
return np.array(enc_tensor.decrypt().tolist())
def bootstrap(context, tensor):
# To refresh a tensor with exhausted depth. 
# Here, bootstrap = enc(dec())
tmp = decrypt(tensor)
return encrypt(context, tmp)
if __name__ == "__main__":
a = np.array([[1.,2.,3.,4.], [1.,2.,5.,4.]])
context = gencontext()
enc_a = encrypt(context, a)
enc_at = encrypt(context, a.T)
enc_b = encrypt(context, a)
res = enc_a + enc_b
# res = enc_a - enc_b
# res = enc_a * enc_b
# res = enc_a @ enc_at
print(decrypt(res))

加密和解密

context = context()
message = [60, 66, 73, 81, 90]
plain_vector = ts.plain_tensor(message)
encrypted_vector = ts.ckks_vector(context, plain_vector)
print(encrypted_vector.decrypt().tolist()) # tolist是用來將多項式m(X)解碼成張量的
# 加法和乘法直接使用+, *, @ 即可
m1 = [1, 2, 3]
m2 = [4, 5, 6]
p1, p2 = ts.plain_tensor(m1), ts.plain_tensor(m2)
e1, e2 = ts.ckks_vector(context, p1), ts.ckks_vector(context, p2)
e1 + e2
e1 * e2
e1 @ e2

0x04 實現細節

理論上CKKS的加解密是這麼操作的，但是實際上還有很多為了性能做出的優化。

向量的編碼

這裡我們要談一下向量編碼的部分，就是這裡做的事情：

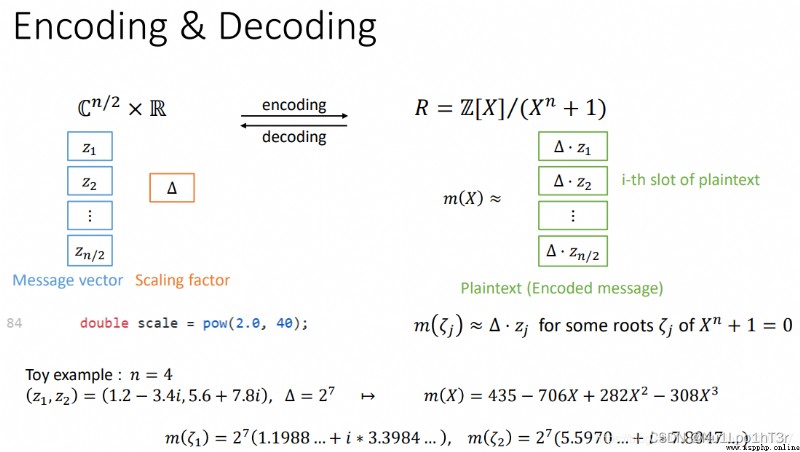
前面說過，這裡我們根據多項式在每個點的值來確定多項式本身的樣子（就是確定多項式的系數）。這個方法其實有很多，比如數值計算方法裡會講到的那幾種插值。

但是，在CKKS中，並不會真正地存儲一個多項式。而是存儲若干的向量對。向量對的內容是：分圓多項式 X N + 1 X^N + 1 XN+1的所有根和拼接了共轭部分的原向量。比如，復向量 ( 1 + 4 i , 5 − 2 i ) (1 + 4i, 5 - 2i) (1+4i,5−2i)。增廣後的結果是 ( 1 + 4 i , 5 − 2 i , 1 − 4 i , 5 + 2 i ) (1 + 4i, 5 - 2i, 1-4i, 5+2i) (1+4i,5−2i,1−4i,5+2i)。存儲在計算機中的結果就是 X 4 + 1 = 0 X^4+1=0 X4+1=0的四個根（前兩個和後兩個共轭）以及 ( 1 + 4 i , 5 − 2 i , 1 − 4 i , 5 + 2 i ) (1 + 4i, 5 - 2i, 1-4i, 5+2i) (1+4i,5−2i,1−4i,5+2i) 捏在一塊構成的向量對。

為什麼這麼做呢，因為如果真的存儲了多項式（在計算機裡面是存儲多項式的各項系數），那麼做乘法會是一件十分麻煩的事情。我記得數據結構中有一道經典的題目，就是用鏈表實現多項式乘法。感興趣的可以試著實現一下體驗體驗難度。由於涉及大量的同類項合並，所以算起來十分難受。此外在CKKS中，做了多項式乘法還意味著要做多項式的重線性化，反正我是不想動手實現的。

於是密文乘法就直接乘對應的增廣向量就完事了，連重線性化都不需要做。有一個定理保證了上面這些事的正確性：n-1次多項式最多有n個根。