本文已參與「新人創作禮」活動,一起開啟掘金創作之路.
送什麼禮物才能讓女人滿意,男人苦不堪言.像我這種有選擇恐懼症的,每當節日來臨一堆東西擺在面前都不知道挑啥(bushi,確實我還沒有女友,落淚).干脆就整個AHP幫咱挑選一個適合送給對象或者自己(也要愛自己喔~)的禮物,AHP原理其實都不需要理解,咱們會實際運用就貼切了,想要理解更多的歡迎看看我的博客有詳解喔:層次分析法(AHP)原理以及應用.廢話不多說了咱們開始吧!
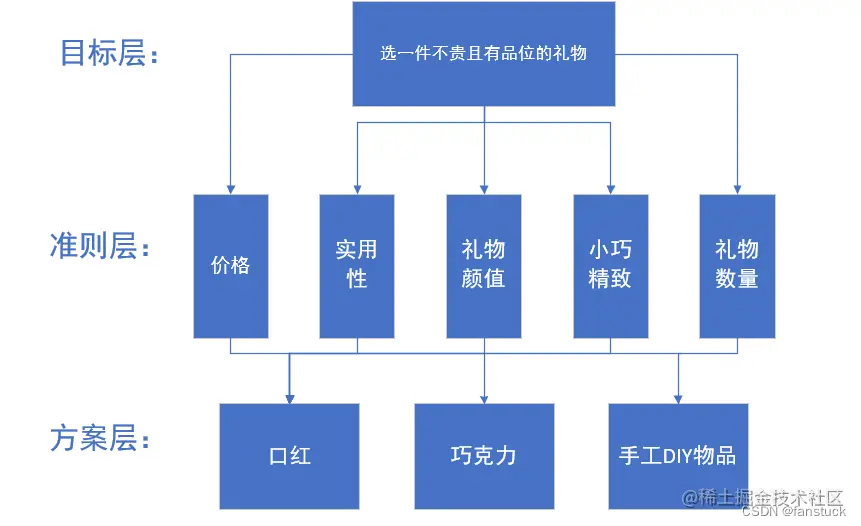
第一步我們需要確定我們的目標是什麼,是選擇個高端大氣上檔次的禮物呢,還是選擇個低調奢華有內涵的禮物. 確定了我們需要挑選啥禮物的目標,會影響後續挑選禮物品質的打分.所以我們需要確定要挑選哪種品質的禮物.像我這種純純碼農來說一般喜歡那種不貴且看上去很有內涵也上檔次的禮物(是不是要求太高了).當然大家可以自己決定想要什麼,這裡我先根據本人的目標來,大家看會一遍後自己就能做出來了:

第二步我們需要思考一些禮物的屬性,也就是我們一般衡量禮物的價值要考慮到的東西.比如貴不貴啊、顏值咋樣、精准小巧、實用性高啊等等.這些將屬性影響到我們最終選擇什麼禮物,當然就是建立在各個因素對比之上.首先我們確定要選擇禮物的考慮品質:
 當然大家也可以自行選擇不同的考慮因素.
當然大家也可以自行選擇不同的考慮因素.
第三步也就是供我們選擇具體送的哪種類型的禮物,如巧克力、鮮花、口紅、化妝品、游戲(、手表包包等等.
 這幾個禮物應該是目前最熱門的吧,現在鮮花都不能當面送了有點可惜,當然大家可以根據自己想送的禮物來衡量.
這幾個禮物應該是目前最熱門的吧,現在鮮花都不能當面送了有點可惜,當然大家可以根據自己想送的禮物來衡量.
這樣一來我們就建立了層次模型了:
1.構建對比矩陣 咱們提出了考慮因素和禮物當然要進行對比了,這裡我們不是把所有因素加起來一起比較,而是兩兩進行比較:
不把所有因素放在一起比較,而是兩兩相互比較. 對此時采用相對尺度,以盡可能減少性質不同的諸因素相互比較的困難,以提高准確度. 這裡我們需要用到兩兩因素對比之間衡量二者重要性的標度:

現在我們要根據考慮因素來衡量一些各個因素之間到底哪個對於我們最終選擇的目標最值得考慮:
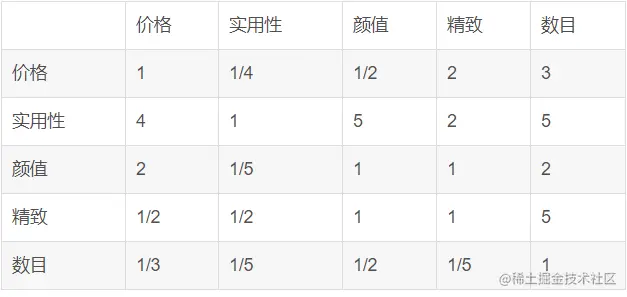 這裡需要自己主觀對比打分.
這裡需要自己主觀對比打分.
接下來我們需要通過列向量歸一化和行向量歸一化獲取權向量,過程其實很簡單並不復雜:
我們依據矩陣來看:矩陣為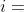 行
行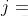 列,這第一行第一列就是
列,這第一行第一列就是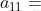 ,那麼列向量歸一化運算就是把第一行第一個元素進行:
,那麼列向量歸一化運算就是把第一行第一個元素進行: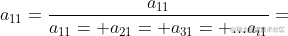 . 根據此運算我們把上述矩陣進行列向量歸一化:
. 根據此運算我們把上述矩陣進行列向量歸一化:
import numpy as np
a=np.array([1,4,2,0.5,1/3])
b=np.array([1/4,1,0.2,0.5,0.2])
c=np.array([1/2,5,1,1,0.5])
d=np.array([2,2,1,1,0.2])
e=np.array([3,6,2,5,1])
a/a.sum()
b/b.sum()
c/c.sum()
d/d.sum()
e/e.sum()
復制代碼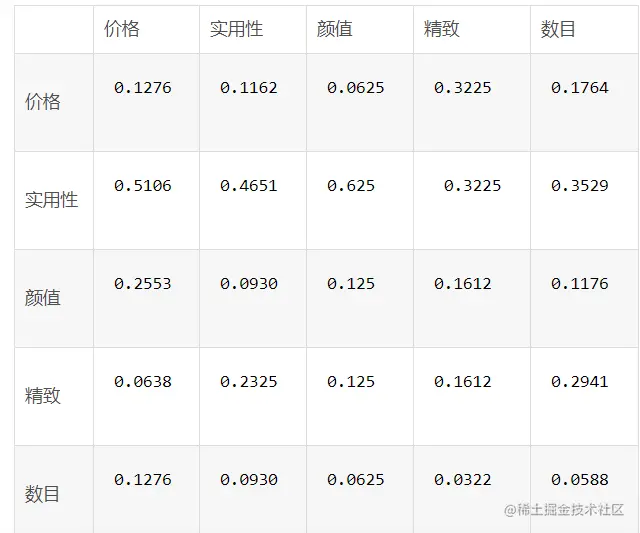
行和歸一化為每行的數相加除以每行的個數,這裡進行降維轉為i行1列的矩陣,計算公式為:
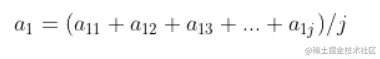
np.sum(ep,axis=1)/5
array([0.16109798, 0.45525528, 0.15045596, 0.17535918, 0.05783161])
復制代碼這便得到了我們的權向量.
我們假設特征值為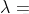 ,則線性代數特征公式為
,則線性代數特征公式為 ,其中
,其中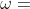 為權向量.
為權向量.
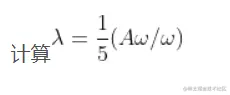
b=np.array([1/4,1,0.2,0.5,0.2])
c=np.array([1/2,5,1,1,0.5])
d=np.array([2,2,1,1,0.2])
e=np.array([3,6,2,5,1])
em=np.array([a,b,c,d,e])
a=a/a.sum()
b=b/b.sum()
c=c/c.sum()
d=d/d.sum()
e=e/e.sum()
ep=np.array([a,b,c,d,e]).T
ex=np.sum(ep,axis=1)/5
lamda=np.matmul(ex,em)/ex
lamda.sum()*1/5
復制代碼得到最大特征根:
復制代碼現在我們需要鞏固計算出來的成果,是否具有科學性和可靠性.這時候我們需要進行一致性檢驗,驗證我們的模型是否具有說服力.
一致性檢驗原理: 檢驗我們構造的判斷矩陣和一致矩陣是否有太大的差別. 1.第一步計算CI 我們需要計算衡量一致性的指標:
我們需要計算衡量一致性的指標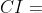 :
: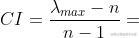
 ,有完全的一致性;
,有完全的一致性;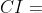 接近於0,有滿意的一致性;
接近於0,有滿意的一致性;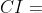 越大,不一致越嚴重 為了衡量
越大,不一致越嚴重 為了衡量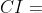 的大小,引入隨機一致性指標
的大小,引入隨機一致性指標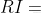
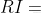
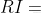 的值根據n的大小來決定:
的值根據n的大小來決定:

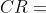
一般,當一致性比率 時,認為A的不一致程度在容許范圍之內,有滿意的一致性,通過一致性檢驗.可用其歸一化特征向量作為權向量,否則要重新構造成對比較矩陣A,對
時,認為A的不一致程度在容許范圍之內,有滿意的一致性,通過一致性檢驗.可用其歸一化特征向量作為權向量,否則要重新構造成對比較矩陣A,對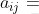 加以調整.
加以調整.
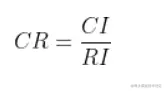 這裡我們的判斷矩陣計算結果為:
這裡我們的判斷矩陣計算結果為:

 ,通過一次性檢驗.
,通過一次性檢驗.
接下來我們要根據三種選擇方案:口紅、巧克力和手工DIY禮品來進行逐個影響因素對比.計算方法是和計算准則層方法一樣的,這裡便不再逐步進行計算:
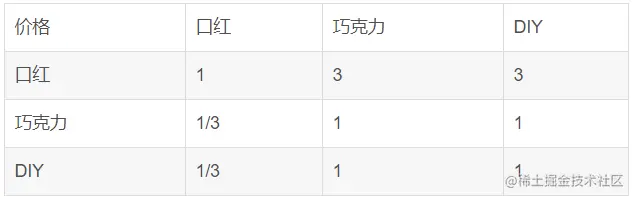


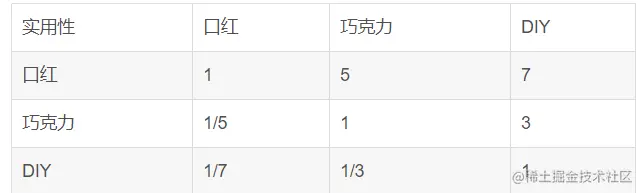

 接下來大家可自行對比打分,這裡不逐個演示了,直接進行填充權重矩陣:
接下來大家可自行對比打分,這裡不逐個演示了,直接進行填充權重矩陣:
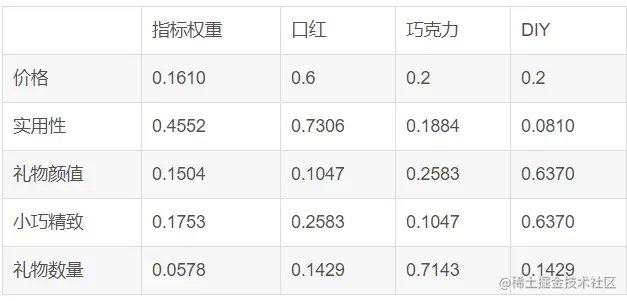 最終計算各個方案的得分: 口紅:
最終計算各個方案的得分: 口紅:
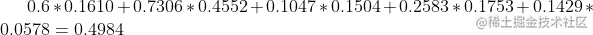 巧克力:
巧克力: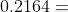 DIY:0.2848
DIY:0.2848
以上就是本期全部內容.我是fanstuck ,有問題大家隨時留言討論 ,我們下期見.