本文已參與「新人創作禮」活動,一起開啟掘金創作之路.
最近在學習這本書《機器學習實戰》,The third chapter is the content of the decision tree,概念非常簡單,But the implementation according to the different clustering situation to make a different to adjust a little difficult.Of course take some algorithm and machine learning is not very good at some libraries to master,To improve their programming combined with the ability to.I have many uncertain questions in this field,Article may have some mistakes,望大家在評論區指正,This article errors will constantly correcting maintenance.
決策樹(Decision Tree）是在已知各種情況發生概率的基礎上,通過構成決策樹來求取淨現值的期望值大於等於零的概率,評價項目風險,判斷其可行性的決策分析方法,是直觀運用概率分析的一種圖解法.由於這種決策分支畫成圖形很像一棵樹的枝干,故稱決策樹.在機器學習中,決策樹是一個預測模型,他代表的是對象屬性與對象值之間的一種映射關系.
分類樹（決策樹）是一種十分常用的分類方法.他是一種監督學習,所謂監督學習就是給定一堆樣本,每個樣本都有一組屬性和一個類別,這些類別是事先確定的,那麼通過學習得到一個分類器,這個分類器能夠對新出現的對象給出正確的分類.這樣的機器學習就被稱之為監督學習.
機器學習中,決策樹是一個預測模型;他代表的是對象屬性與對象值之間的一種映射關系.樹中每個節點表示某個對象,而每個分叉路徑則代表的某個可能的屬性值,而每個葉結點則對應從根節點到該葉節點所經歷的路徑所表示的對象的值.決策樹僅有單一輸出,若欲有復數輸出,可以建立獨立的決策樹以處理不同輸出.數據挖掘中決策樹是一種經常要用到的技術,可以用於分析數據,同樣也可以用來作預測.
從數據產生決策樹的機器學習技術叫做決策樹學習, 通俗說就是決策樹.
一個決策樹包含三種類型的節點：
決策節點：通常用矩形框來表示
機會節點：通常用圓圈來表示
終結點：通常用三角形來表示
決策樹學習也是資料探勘中一個普通的方法.在這裡,每個決策樹都表述了一種樹型結構,它由它的分支來對該類型的對象依靠屬性進行分類.每個決策樹可以依靠對源數據庫的分割進行數據測試.這個過程可以遞歸式的對樹進行修剪. 當不能再進行分割或一個單獨的類可以被應用於某一分支時,遞歸過程就完成了.另外,隨機森林分類器將許多決策樹結合起來以提升分類的正確率.
An overview of the general see text is a bit difficult,Then let's see how it works is well understood.
The working principle of decision tree is similar to you ask me a narrow range,The user to enter a series of data,And then give their preferences.A bit like learning beforeCGuess the leap year similar small algorithm.
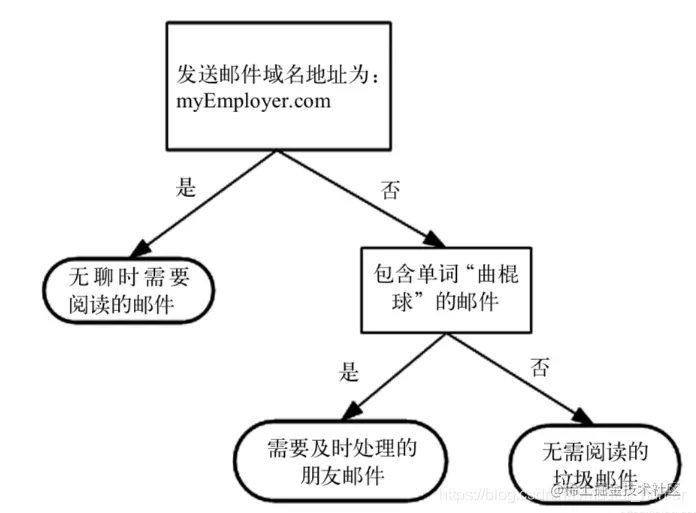決策樹的主要優勢就在於數據形式非常容易理解.因此決策樹可以使用不熟悉的數據集合,並從中提取出一系列規則. 決策樹的特點：
在構造決策樹時,We want to catch problems,Also is to get the answer key questions,劃分出最好的結果.因此我們必須評估每個特征,Find out the optimal partitioning results.根據決策樹[偽代碼]可知：
From the analysis on the algorithm is a recursive classification algorithm,有三種情況會導致遞歸返回：
1.The branch of attribute data for all kind of,則停止劃分.
2.When all the questions asked characteristics,Feature list is empty,則停止劃分,Most election attribute frequency as leaf nodes.
3.當前節點包含的樣本集合為空,Mark the current node to leaf node,And its categories of sample set as the parent node contains the most categories.
To understand the basic working principle and the method to construct the decision tree after,Now to learn how to deal with the data to make more efficiency use by decision tree.劃分數據集的大原則是：Data will not need to become more orderly.We have to find the character of classified data set the key,Is also the most efficient to ask others to distinguish the categories of problems.First of all we have to have a information about how to measure the orderly degree of variable.
信息熵：Do not make too much explanation about thermodynamics here,Only for information.Information entropy for positioning information expectations.假定當前樣本集合D中第k類樣本所占的比例為pk(k = 1,2,...,|Y|),則D的信息熵定義為：
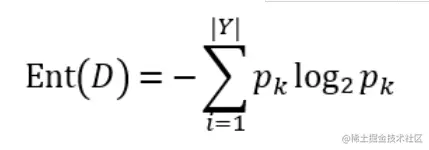For the base number is take2,一般的理解是,Because the information in accordance with the said computer USES is binary form.由定義可推知,Ent(D)的值越小,則D的純度越高. 在理解信息增益之前,要明確——條件熵 信息增益表示得知特征X的信息而使得類Y的信息不確定性減少的程度.
條件熵H ( Y ∣ X ) H(Y|X)H(Y∣X)表示在已知隨機變量X的條件下隨機變量Y的不確定性,隨機變量X給定的條件下隨機變量Y的條件熵(conditional entropy) H(Y|X),定義X給定條件下Y的條件概率分布的熵對X的數學期望：
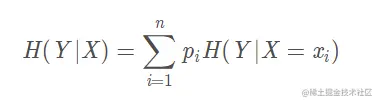其中,
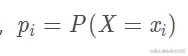
當熵和條件熵中的概率由數據估計（特別是極大似然估計）得到時,所對應的分別為經驗熵和經驗條件熵,此時如果有0概率,令0log0=0. 在此基礎上,給出 “信息增益”（information gain） 的定義： 假定離散屬性a有V種不同的取值{a1, a2, ..., aV},使用a對D進行劃分,則會產生V個分支節點,其中第vA branch node containsD中屬性值為av的樣本,記為Dv,則用屬性a對樣本集D進行劃分所獲得的信息增益定義為:
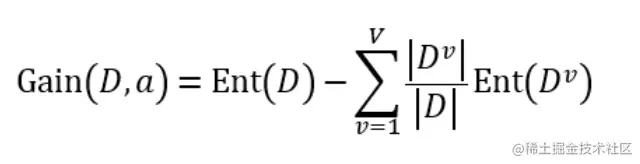一般而言,信息增益越大,則意味著使用屬性a來進行劃分所獲得的純度提升越大.於是,We can according to the information gain to select the division of decision tree properties.Related algorithm is the famousID3算法[Quinlan, 1986].
然而事實上,信息增益對可取值數目較多的屬性有所偏好.This preference may reduce model generalization ability.為減少這種偏好帶來的不利影響,著名的C4.5決策樹算法[Quinlan, 1993]不直接使用信息增益,而使用“增益率”（gain ratio）來劃分最優屬性.It introduces the concept of gain rate below.
Because we only use information gain data set divided into,Two other measure gain rate and the gini coefficient should not be too much to explain
To understand the basic knowledge about above can build a tree,With missing values in decision tree pruning process and continuous optimization problems such as not discussed before.
Here we simulate a small data：
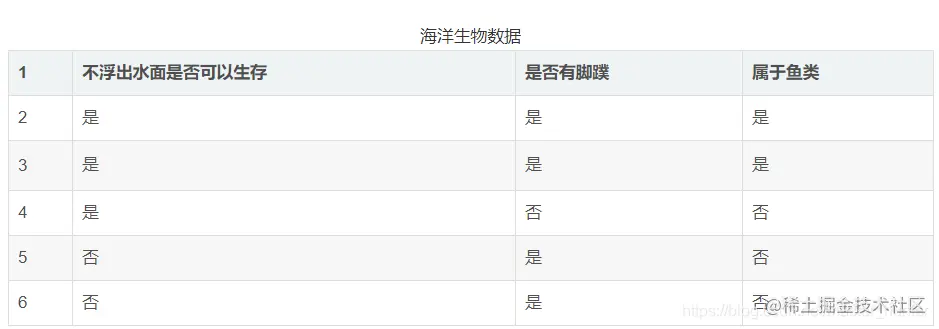According to these data we slowly to construct the decision tree,Finally realize the main function.
The above data into the list,Of course example data is simple,Other data with different processing. ``
dataSet = [[1,1,'yes'],
[1,1,'yes'],
[1,0,'no'],
[0,1,'no'],
[0,1,'no']]
labels = ['no surfacing ','flippers']
return dataSet,labels
復制代碼It is best to use for this class data classification data dictionary to store the classification results.
numEntries = len(dataSet)
labelCounts = {} #創建記錄不同分類標簽結果多少的字典
#為所有可能分類保存
#該字典key：label value:label的數目
for featVec in dataSet:
currentLabel = featVec[-1]
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
shannonEnt = 0.0
for key in labelCounts:
prob = float(labelCounts[key])/numEntries #標簽發生概率p(xi)的值
shannonEnt -= prob * log(prob,2)
return shannonEnt #熵
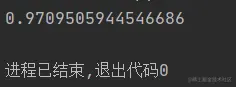
復制代碼Code implementation and the entropy calculation agree.Test the data set before classification entropy：
Of course can alter according to the original data set label to test the volatility of entropy：
Can be found that the higher the data more entropy.
#Avoid modifying the original data set to create a new data set
retDataSet = []
#Extract conforms to the characteristics of the data set
for featVec in dataSet:
if featVec[axis] == value:
reducedFeatVec = featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSet
復制代碼Can say is selected in accordance with characteristics of the data set and then thrown own characteristic value list.
We can try：
print(a)
復制代碼[[1, 'yes'], [1, 'yes'], [0, 'no']]
如何就是決策樹的重點,如何選擇最優的劃分方式,也就是選擇信息增益最大化的方式,通過for循環對不同的特征值進行劃分,計算每種方式的信息熵,然後取得最大信息增益劃分方式,計算最好的信息增益,返回最好特征劃分的索引值.
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0])-1 #全部特征
baseEntropy = calcShannonEnt(dataSet) #基礎熵
bestInfoGain = 0.0
bestFeature = -1
for i in range(numFeatures):
#創建唯一的分類標簽列表
featList = [example[i] for example in dataSet]
uniqueVals = set(featList) #建立列表同特征下不同回答
newEntropy = 0.0
#計算每種劃分方式的信息熵
for value in uniqueVals:
subDataSet = splitDataSet(dataSet,i,value) #劃分
prob = len(subDataSet)/float(len(dataSet)) #同特征下不同回答所占總回答比率
newEntropy += prob * calcShannonEnt(subDataSet) #該特征劃分下的信息熵
infoGain = baseEntropy - newEntropy #信息增益
if ( infoGain > bestInfoGain ):
bestInfoGain =infoGain
bestFeature = i
return bestFeature
復制代碼print(chooseBestFeatureToSplit(MydDat))
復制代碼0 To learn that the best classification features for the first,So for the first time to the first characteristic to ask.
To chart a better understand：
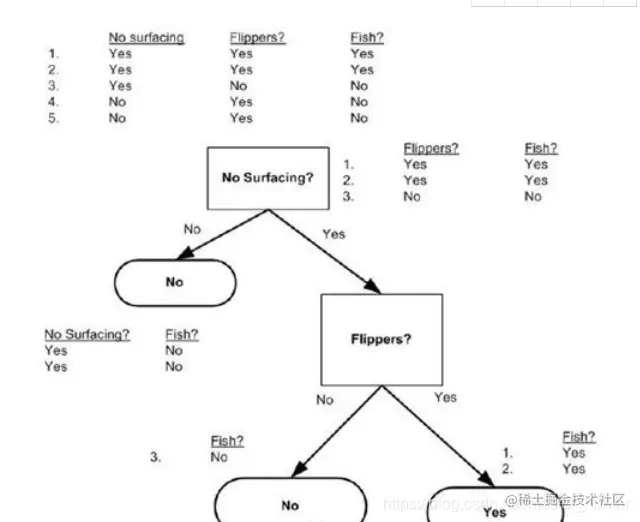Before the structure tree for recursive return conditions the second：When all the questions asked characteristics,Feature list is empty,則停止劃分,Most election attribute frequency as leaf nodes.當遍歷完所有特征時,To return to appear most times classification name.So to construct the election function：
classCount={}
for vote in classList:
if vote not in classCount.key():classCount[vote] = 0
classCount[vote] +=1
sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
return sortedClassCount[0][0]
復制代碼After the recursive structure decision tree：
classList = [example[-1] for example in dataSet] #保存標簽
if classList.count(classList[0]) == len(classList): #如果類別完全相同則停止劃分
return classList[0] #返回出現次數最多的標簽
if len(dataSet[0]) == 1: #遍歷完所有特征時返回出現次數最多的類別
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet)
bestFeatLabel = labels[bestFeat]
myTree= {bestFeatLabel:{}}
del(labels[bestFeat])#Using the characteristics of the cross out
#得到列表包含的所有屬性值
featValues = [example[bestFeat] for example in dataSet]
uniqueVals = set(featValues)
for value in uniqueVals:
subLabels = labels[:]#After dividing feature set
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet,bestFeat,value),subLabels)
return myTree
復制代碼輸出結果為：
{'no surfacing ': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}} The decision tree constructed.
以上就是本期全部內容.我是fanstuck ,有問題大家隨時留言討論 ,我們下期見.
