1. 實驗目的

實現一個 k-means 算法和混合高斯模型，並且用 EM 算法估計模型中的參數。

2. 實驗要求

• 用高斯分布產生 k 個高斯分布的數據（不同均值和方差）（其中參數自己設定）。
  • 用 k-means 聚類，測試效果；
  • 用混合高斯模型和你實現的 EM 算法估計參數，看看每次迭代後似然值變化情況，考察 EM 算法是否可以獲得正確的結果（與你設定的結果比較）。
• 應用：可以 UCI 上找一個簡單問題數據，用你實現的 GMM 進行聚類。

3. 設計思想

3.1 K-means 算法

k 均值聚類算法（k-means clustering algorithm）是一種迭代求解的聚類分析算法，其步驟是，預將數據分為 K 組，則隨機選取 K 個對象作為初始的聚類中心，然後計算每個對象與各個種子聚類中心之間的距離，把每個對象分配給距離它最近的聚類中心。聚類中心以及分配給它們的對象就代表一個聚類。每分配一個樣本，聚類的聚類中心會根據聚類中現有的對象被重新計算。這個過程將不斷重復直到滿足某個終止條件。終止條件可以是沒有（或最小數目）對象被重新分配給不同的聚類，沒有（或最小數目）聚類中心再發生變化，誤差平方和局部最小。

算法為：先隨機選取 K 個對象作為初始的聚類中心。然後計算每個對象與各個種子聚類中心之間的距離，把每個對象分配給距離它最近的聚類中心。聚類中心以及分配給它們的對象就代表一個聚類。一旦全部對象都被分配了，每個聚類的聚類中心會根據聚類中現有的對象被重新計算。這個過程將不斷重復直到滿足某個終止條件。終止條件可以是以下任何一個：

• 沒有（或最小數目）對象被重新分配給不同的聚類。
• 沒有（或最小數目）聚類中心再發生變化。
• 誤差平方和局部最小。

3.2 GMM 算法

GMM，高斯混合模型，也可以簡寫為 MOG。高斯模型就是用高斯概率密度函數（正態分布曲線）精確地量化事物，將一個事物分解為若干的基於高斯概率密度函數（正態分布曲線）形成的模型。

GMM 相對 K-means 是比較復雜的 EM 算法的應用實現。與 K-means 不同的是，GMM 算法在 E 步時沒有使用“最近距離法”來給每個樣本賦類別（hard assignment），而是增加了隱變量 γ。γ 是(N,K)的矩陣， γ[N,K]表示第 n 個樣本是第 k 類的概率，因此， 具有歸一性。即 的每一行的元素的和值為 1。

GMM 算法是用混合高斯模型來描述樣本的分布，因為在多類情境中，單一高斯分布肯定是無法描繪數據分布。多個高斯分布的簡單疊加也無法描繪數據分布的。只有混合高斯分布才能較好的描繪一組由多個高斯模型產生的樣本。對於樣本中的任一個數據點，任一高斯模型能夠產生該點的概率，也就是任一高斯模型對該點的生成的貢獻（contribution）是不同的，但可以肯定的是，這些貢獻的和值是 1。

4. 實驗過程

4.1 算法設計

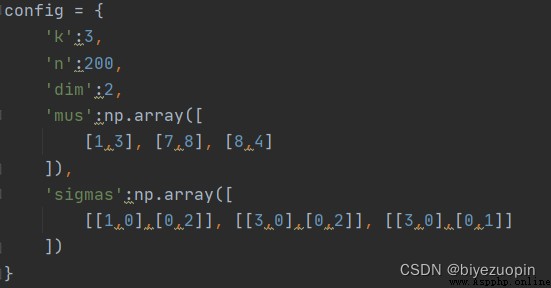
高斯分布參數：

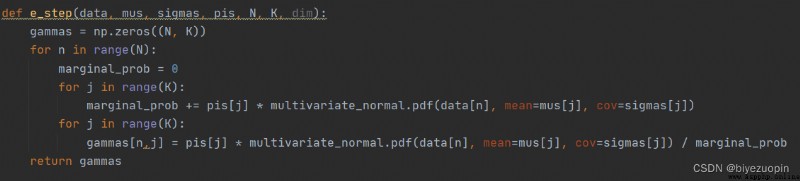
E 步：

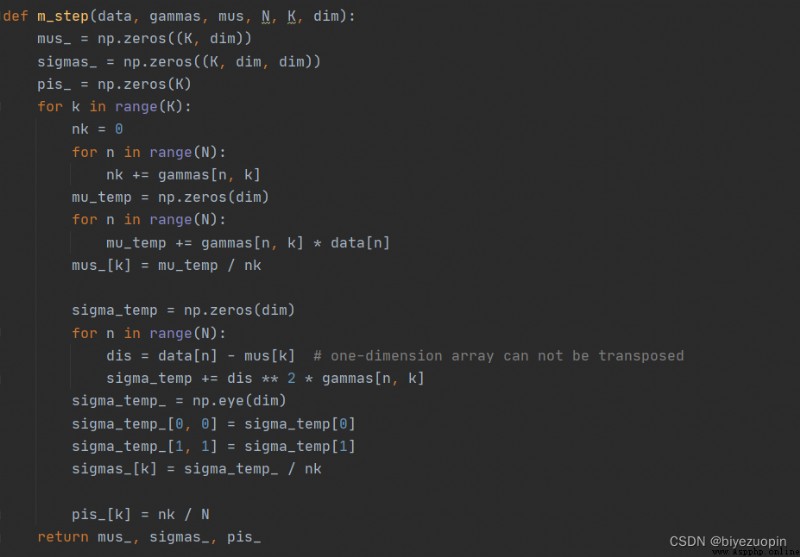
M 步：

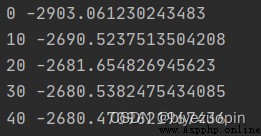
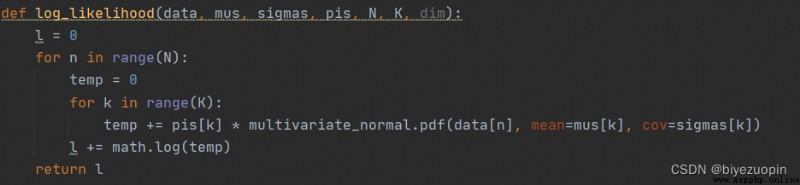
極大似然估計：

4.2 實驗結果

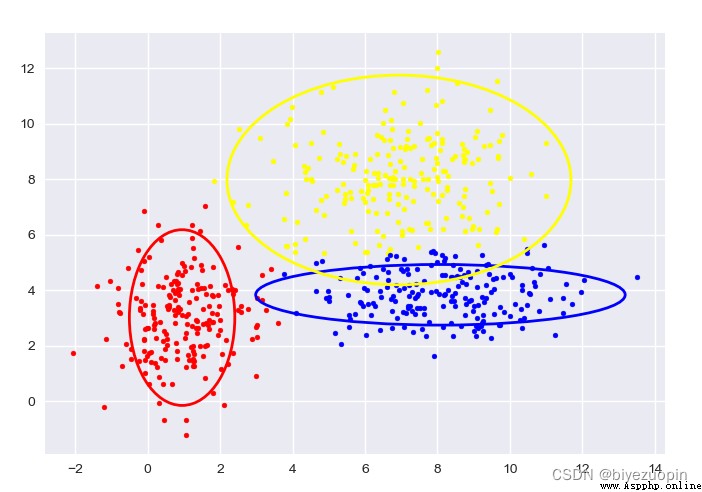
自生成數據，K-means：

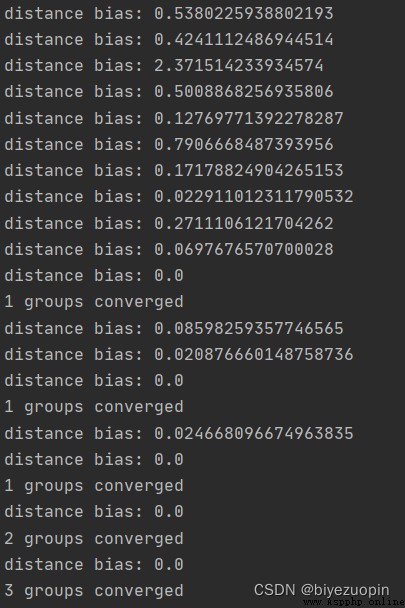
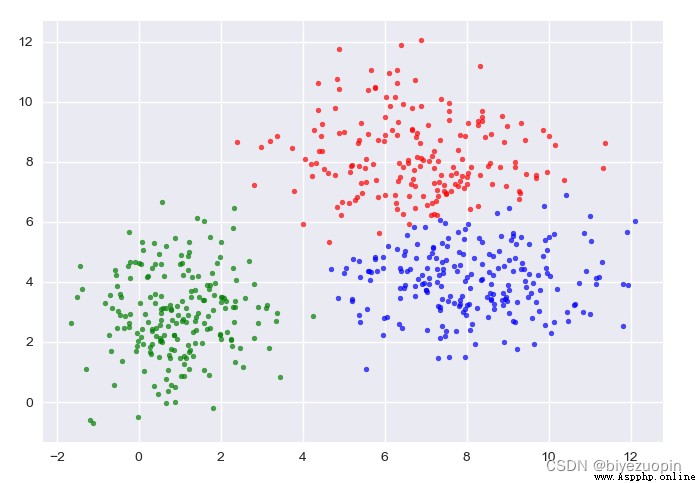
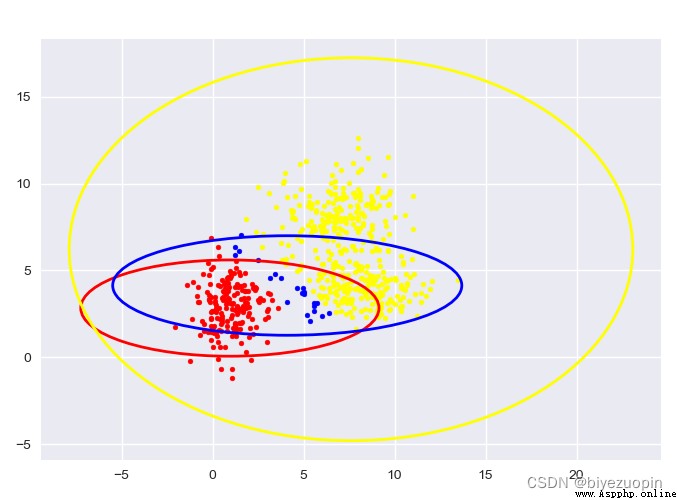
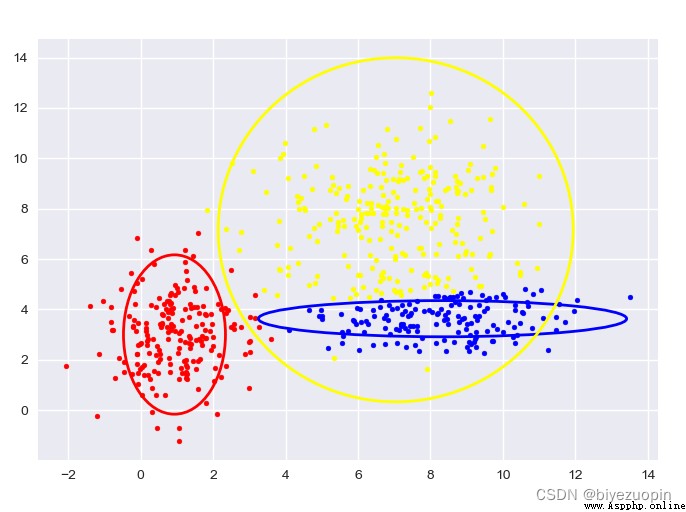
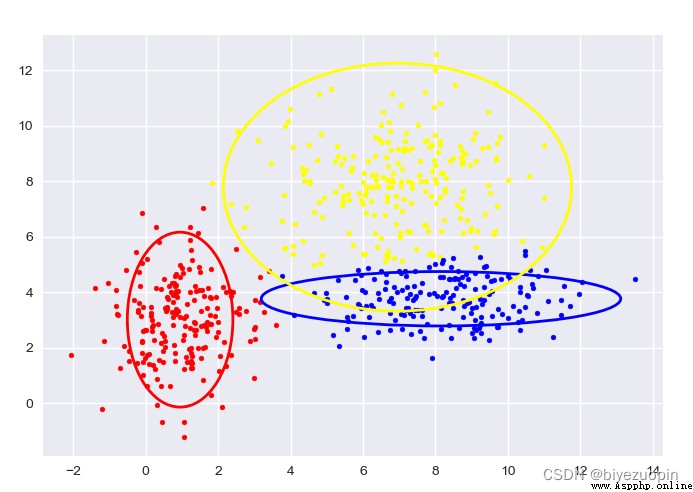
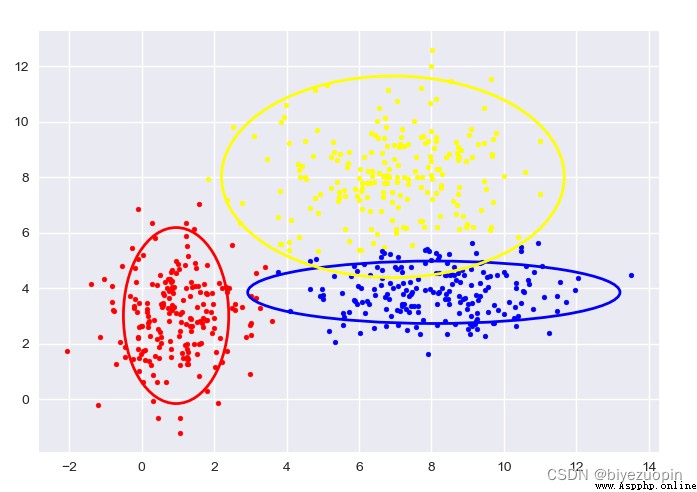
自生成數據，GMM：

圖中給出了每一階段的樣本分類情況和置信橢圓。

最後帶有填充的透明置信橢圓為生成數據的真實橢圓。