1. 實驗目的

理解邏輯回歸模型，掌握邏輯回歸模型的參數估計算法。

2. 實驗要求

實現兩種損失函數的參數估計（1.無懲罰項；2.加入對參數的懲罰），可以采用梯度下降、共轭梯度或者牛頓法等。

驗證：

• 可以手工生成兩個分別類別數據（可以用高斯分布），驗證你的算法。考察類條件分布不滿足樸素貝葉斯假設，會得到什麼樣的結果。
• 邏輯回歸有廣泛的用處，例如廣告預測。可以到 UCI 網站上，找一實際數據加以測試。

3. 實驗內容

3.1 算法原理

我們分類器做分類問題的實質，就是預測一個已知樣本的位置標簽，即 P(Y=1|x < x1, … , xn)。按照樸素貝葉斯的方法，可以用貝葉斯概率公式，將其轉化為類條件概率（似然）和類概率的乘積。這次實驗，是直接求該概率。

經過推導我們可以得到：

定義 sigmoid 函數為：

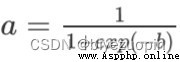
計算損失函數為：

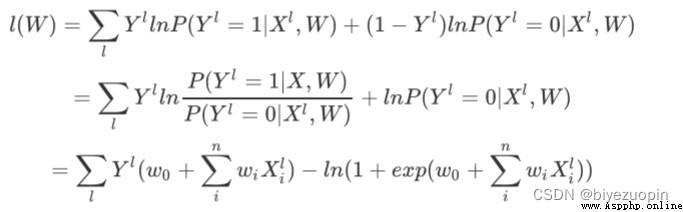
用梯度下降法求得 W = argmaxwl(w)，注意要用梯度下降的話，一般要把這裡的 l(w)轉化為相反數，-l(w)作為損失函數，求其最小值。

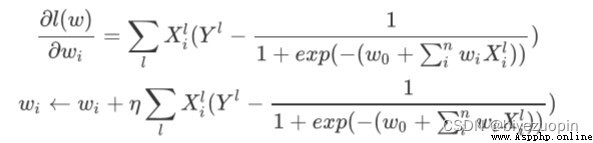
而我們加上正則項的梯度下降為

3.2 算法的實現

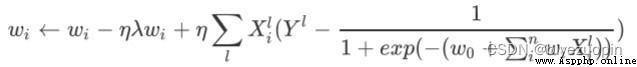
首先是生成數據，如果要生成類條件分布滿足樸素貝葉斯假設的數據，那麼就對每一個類別的每一個維度都用一個獨立的高斯分布生成。如果要生成類條件分布不滿足樸素貝葉斯假設的數據，那麼 就對每一個類別的兩個維度用一個二維高斯分布生成。需要注意的是，由於高斯分布具有的特性， 多維高斯分布不相關可以推出獨立性，因此，可以用二維高斯分布生成數據，如果是滿足樸素貝葉斯假設的，那麼協方差矩陣的非對角線元素均為 0，如果是不滿足樸素貝葉斯假設的，那麼協方差矩陣的非對角線元素不為 0（協方差矩陣應該是對稱陣）。

計算極大似然估計:

梯度下降算法：

在做 UCI 上的數據時，選取了皮膚 Skin_NonSkin.txt 數據。由於該數據量太大，這裡只選取了其中一部分。

讀取數據時，用 numpy 切片提取數據信息，用 50 作為步長，提取部分數據用做實驗。還要對樣本點進行空間平移，否則在計算 MCLE 時可能會溢出，因為計算 MCLE 時，要用參數與樣本做矩陣乘法，而且還要作為的指數計算，可能會溢出。

4. 實驗結果

自己生成數據

類條件概率滿足樸素貝葉斯假設，正則項 λ=0，size=200

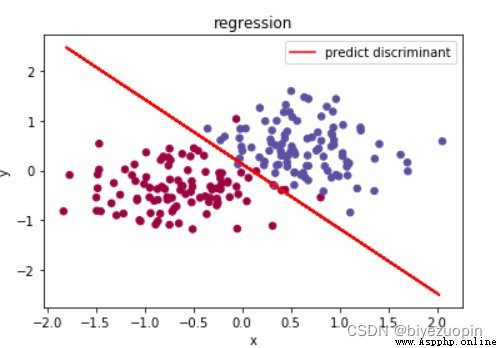
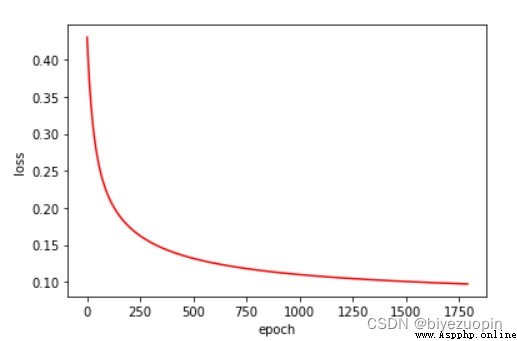
類條件概率不滿足樸素貝葉斯假設，正則項 λ=0，size=200

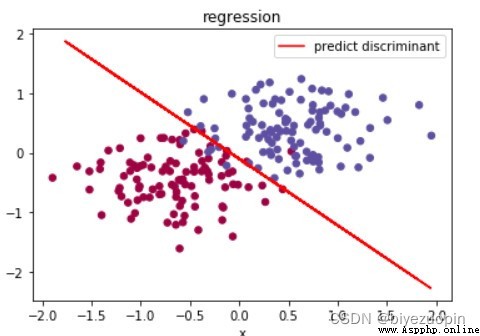
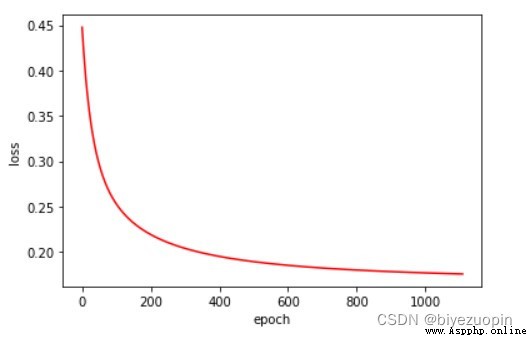
類條件分布滿足樸素貝葉斯假設，正則項 λ=0.001，size=200

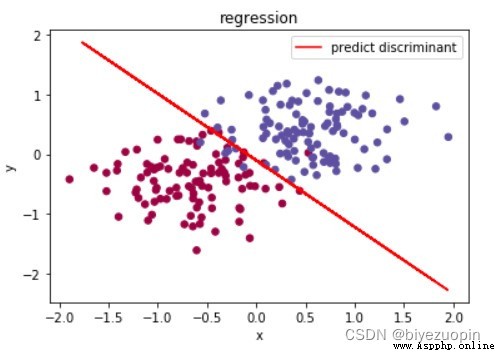
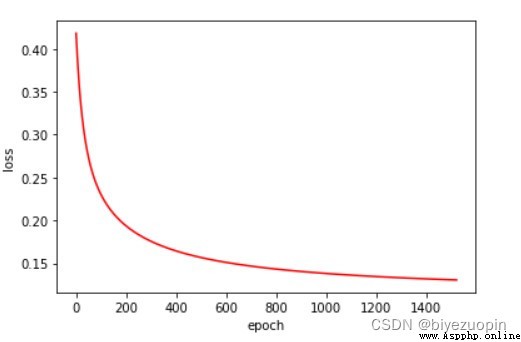
類條件概率不滿足樸素貝葉斯假設，正則項 λ=0.001，size=200

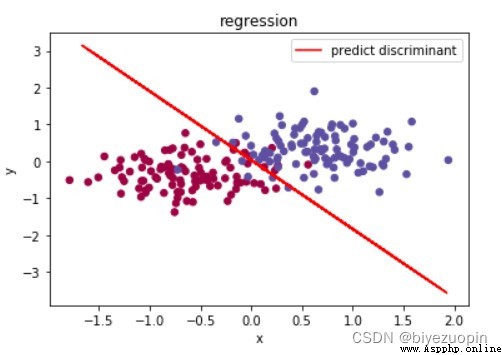
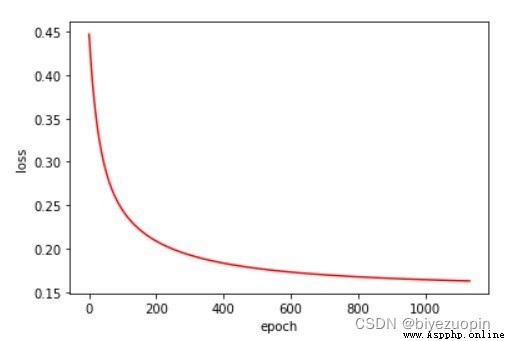
UCI 皮膚顏色數據集

正則項 λ=0

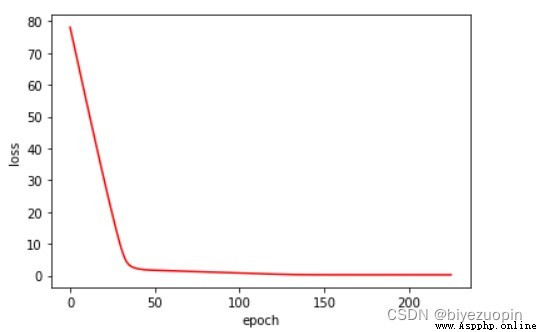
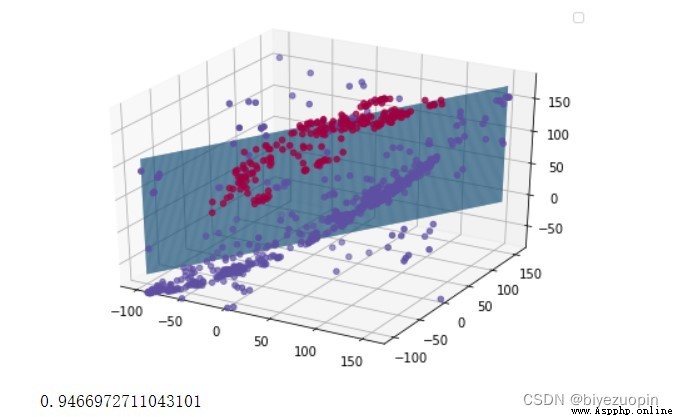
正則項 λ=0.01

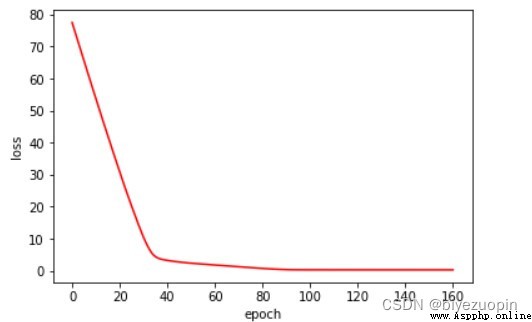
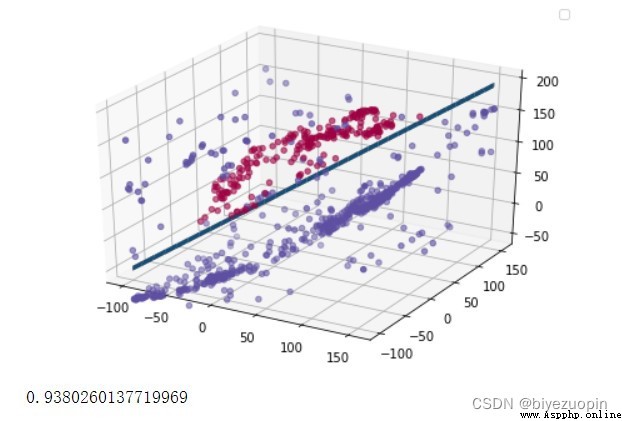
UCI banknote 數據集

正則項 λ=0

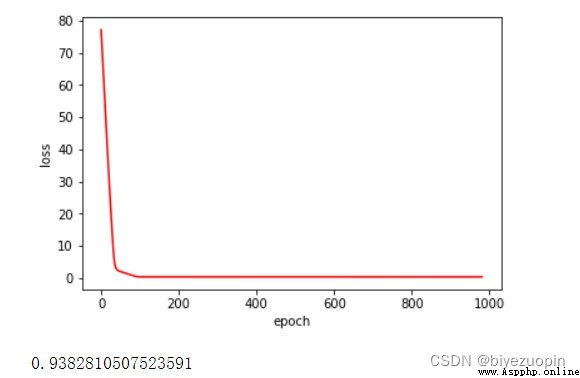
正則項 λ=0.01

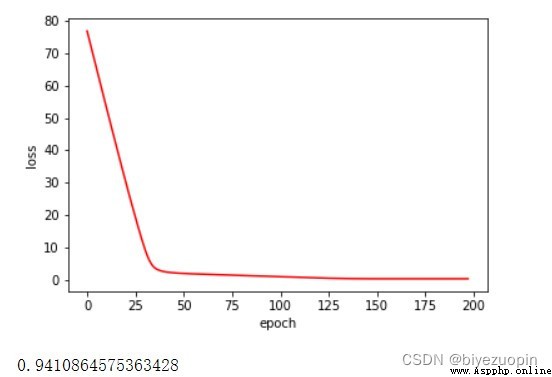
實驗發現，UCI 的數據的 20% 測試集的准確率基本穩定在 93%-94%。 正則項在數據量較大時，對結果的影響不大，在數據量較小時， 應可以有效解決過擬合問題。 類條件分布在滿足樸素貝葉斯假設時的分類表現，要比不滿足假設時略好。 logistics 回歸可以很好地解決簡單的線性分類問題，而且收斂速度較快。
量較大時，對結果的影響不大，在數據量較小時， 應可以有效解決過擬合問題。 類條件分布在滿足樸素貝葉斯假設時的分類表現，要比不滿足假設時略好。 logistics 回歸可以很好地解決簡單的線性分類問題，而且收斂速度較快。