目錄
滿二叉樹
完全二叉樹
堆
堆的向下調整
堆的排序過程
代碼實現
時間復雜度
如果二叉樹中除了葉子結點,每個結點的度都為 2,則此二叉樹稱為滿二叉樹。
如果二叉樹中除去最後一層節點為滿二叉樹,且最後一層的結點依次從左到右分布,則此二叉樹被稱為完全二叉樹。
1.必須是完全二叉樹
2.用數組實現
3.任一結點的值是其子樹所有結點的最大值或最小值
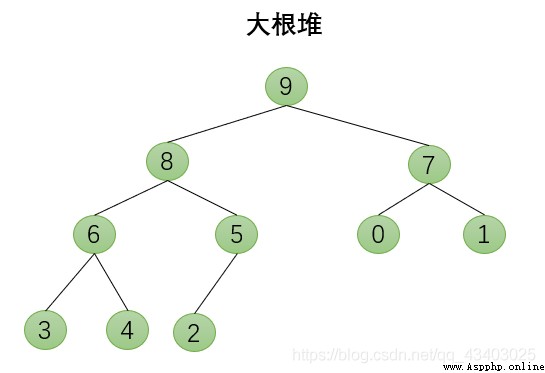
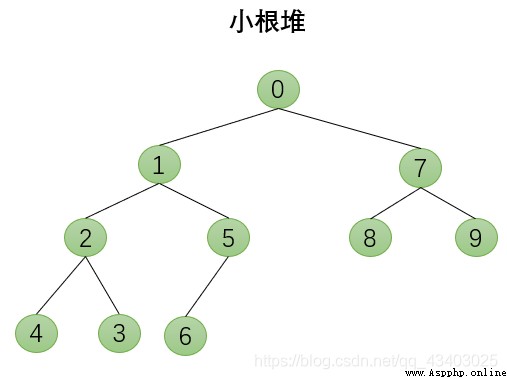
節點的左右子樹都是堆,但自身不是堆的二叉樹才能向下調整,最終變成堆
挨個出數:1、將帶列構造成一個大頂堆,根據大頂堆的性質,當前堆的根節點(堆頂)就是序列中最大的元素;2、將堆頂元素和最後一個元素交換,然後將剩下的節點重新構造成一個大頂堆;3、重復步驟2,如此反復,從第一次構建大頂堆開始,每一次構建,我們都能獲得一個序列的最大值,然後把它放到大頂堆的尾部。
def sift(li,low,high): #low根節點 high最後一個節點
i=low #i開始指向根節點
j=2*i+1 #j是左孩子
tmp=li[low] #堆頂的值
while j<=high:
if j+1<=high and li[j+1]>li[j]:
j=j+1
if li[j]>tmp:
li[i]=li[j]
i=j
j=2*i+1
else:
li[i]=tmp
break;
else :
li[i]=tmp
def heap_sort(li):
n=len(li)
for i in range((n-2)//2,-1,-1):
sift(li,i,n-1)
for i in range(n-1,-1,-1):
li[0],li[i]=li[i],li[0]
sift(li,0,i-1)
li= [i for i in range(10)]
import random
random.shuffle(li)
print(li)
heap_sort(li)
print(li)

O(nlogn)