Table of Contents
Full binary tree
complete binary tree
heap
Heap down adjustment
The sorting process of the heap
Code Implementation
Time complexity
If the degree of every node in the binary tree is 2 except for the leaf nodes, then the binary tree is called a full binary tree.
If the last layer of nodes in the binary tree is full, and the nodes of the last layer are distributed from left to right in turn, the binary tree is called a complete binary tree.
1. Must be a complete binary tree
2. Implemented with an array
3. The value of any node is the maximum or minimum value of all nodes in its subtree
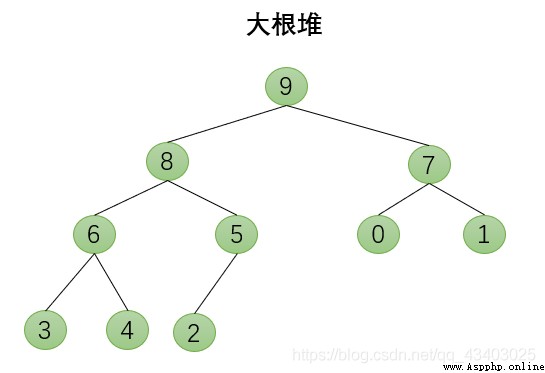
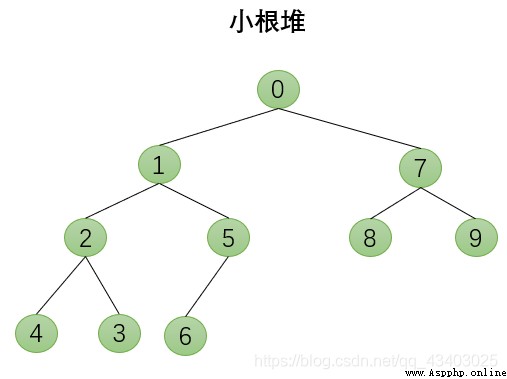
The left and right subtrees of the node are all heaps, but the binary tree that is not itself a heap can be adjusted downward and eventually become a heap
Count out one by one: 1. Construct the band column into a large top heap. According to the nature of the large top heap, the root node (heap top) of the current heap is the largest element in the sequence; 2. Combine the top element and the lastSwap an element, and then reconstruct the remaining nodes into a large top heap; 3. Repeat step 2, and so on, starting from the first construction of the large top heap, each time we build, we can get the maximum value of a sequence, then put it at the end of the big top pile.
def sift(li,low,high): #low root node high last nodei=low #i starts to point to the root nodej=2*i+1 #j is the left childtmp=li[low] #The value of the top of the heapwhile j<=high:if j+1<=high and li[j+1]>li[j]:j=j+1if li[j]>tmp:li[i]=li[j]i=jj=2*i+1else:li[i]=tmpbreak;else :li[i]=tmpdef heap_sort(li):n=len(li)for i in range((n-2)//2,-1,-1):sift(li,i,n-1)for i in range(n-1,-1,-1):li[0],li[i]=li[i],li[0]sift(li,0,i-1)li= [i for i in range(10)]import randomrandom.shuffle(li)print(li)heap_sort(li)print(li)
O(nlogn)