Because training word embeddings is computationally time-consuming,所以大多數MLPractitioners load a set of pretrained embeddings.
完成此任務後,你將能夠:
import numpy as np
from w2v_utils import *
Using TensorFlow backend.
接下來,Let's load word vectors.對於此作業,我們將使用50維GloVe向量表示單詞.Run the following cell to loadword_to_vec_map.
words, word_to_vec_map = read_glove_vecs('data/glove.6B.50d.txt')
You have to load:
words:Vocabulary of words.word_to_vec_map:map a word to itsCloVeon a dictionary represented by a vector.你已經看到,One-way vectors do not account for similar words well.GloVeVectors provide more useful information about the meaning of individual words.現在讓我們看看如何使用GloVeA vector determines how similar two words are.
To measure how similar two words are,We need a way to measure the similarity between two embedding vectors of two words.給定兩個向量 u u u和 v v v,余弦相似度定義如下:
CosineSimilarity(u, v) = u ⋅ v ∣ ∣ u ∣ ∣ 2 ∣ ∣ v ∣ ∣ 2 = c o s ( θ ) (1) \text{CosineSimilarity(u, v)} = \frac {u \cdot v} {||u||_2 ||v||_2} = cos(\theta) \tag{1} CosineSimilarity(u, v)=∣∣u∣∣2∣∣v∣∣2u⋅v=cos(θ)(1)
其中 u ⋅ v u \cdot v u⋅v是兩個向量的點積(或內積), ∣ ∣ u ∣ ∣ 2 ||u||_2 ∣∣u∣∣2是向量 u u u的范數(或長度),而 θ \theta θ是 u u u和 v v v之間的夾角.This similarity depends on u u u和 v v v之間的角度.如果 u u u和 v v v非常相似,Their cosine similarity will be close to1;如果它們不相似,The cosine similarity will take smaller values.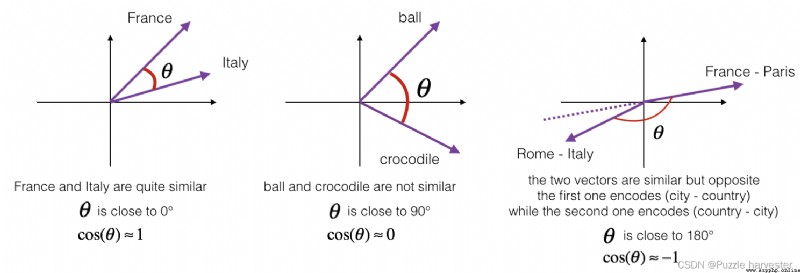
圖1:The cosine of the angle between two vectors indicates their similarity
練習:實現函數cosine_similarity()To assess the vector similarity between words.
提醒: u u u的范數定義為$ ||u||2 = \sqrt{\sum{i=1}^{n} u_i^2}$.
def cosine_similarity(u, v):
""" u與vReflects the cosine similarityu與v的相似程度 參數: u -- 維度為(n,)的詞向量 v -- 維度為(n,)的詞向量 返回: cosine_similarity -- defined by the above formulau和v之間的余弦相似度. """
distance = 0
# 計算u與v的內積
dot = np.dot(u, v)
#計算u的L2范數
norm_u = np.sqrt(np.sum(np.power(u, 2)))
#計算v的L2范數
norm_v = np.sqrt(np.sum(np.power(v, 2)))
# 根據公式1計算余弦相似度
cosine_similarity = np.divide(dot, norm_u * norm_v)
return cosine_similarity
father = word_to_vec_map["father"]
mother = word_to_vec_map["mother"]
ball = word_to_vec_map["ball"]
crocodile = word_to_vec_map["crocodile"]
france = word_to_vec_map["france"]
italy = word_to_vec_map["italy"]
paris = word_to_vec_map["paris"]
rome = word_to_vec_map["rome"]
print("cosine_similarity(father, mother) = ", cosine_similarity(father, mother))
print("cosine_similarity(ball, crocodile) = ",cosine_similarity(ball, crocodile))
print("cosine_similarity(france - paris, rome - italy) = ",cosine_similarity(france - paris, rome - italy))
cosine_similarity(father, mother) = 0.8909038442893615
cosine_similarity(ball, crocodile) = 0.2743924626137942
cosine_similarity(france - paris, rome - italy) = -0.6751479308174201
Get the right after the expected output,Feel free to modify the input and measure the cosine similarity between other word pairs!Operating around cosine similarity of other inputs will give you a better understanding of the representation of word vectors.
in the analogy task,we complete the sentence"a is to b as c is to __". 一個例子是’man is to woman as king is to queen'. 詳細地說,we try to find a wordd,to make the associated word vectors e a , e b , e c , e d e_a, e_b, e_c, e_d ea,eb,ec,ed通過以下方式相關: e b − e a ≈ e d − e c e_b - e_a \approx e_d - e_c eb−ea≈ed−ec.We will use cosine similarity to measure e b − e a e_b - e_a eb−ea和 e d − e c e_d - e_c ed−ec之間的相似性.
練習:Complete the following code to perform word analogy!
def complete_analogy(word_a, word_b, word_c, word_to_vec_map):
""" 解決“A與Bcomparable toC與____相比一樣”之類的問題 參數: word_a -- a word of type string word_b -- a word of type string word_c -- a word of type string word_to_vec_map -- 字典類型,單詞到GloVe向量的映射 返回: best_word -- 滿足(v_b - v_a) 最接近 (v_best_word - v_c) 的詞 """
# convert word to lowercase
word_a, word_b, word_c = word_a.lower(), word_b.lower(), word_c.lower()
# 獲取對應單詞的詞向量
e_a, e_b, e_c = word_to_vec_map[word_a], word_to_vec_map[word_b], word_to_vec_map[word_c]
# Get all the words
words = word_to_vec_map.keys()
# 將max_cosine_simInitialized to a big negative
max_cosine_sim = -100
best_word = None
# 遍歷整個數據集
for word in words:
# To avoid matching the input data
if word in [word_a, word_b, word_c]:
continue
# 計算余弦相似度
cosine_sim = cosine_similarity((e_b - e_a), (word_to_vec_map[word] - e_c))
if cosine_sim > max_cosine_sim:
max_cosine_sim = cosine_sim
best_word = word
return best_word
triads_to_try = [('italy', 'italian', 'spain'), ('india', 'delhi', 'japan'), ('man', 'woman', 'boy'), ('small', 'smaller', 'large')]
for triad in triads_to_try:
print ('{} -> {} <====> {} -> {}'.format( *triad, complete_analogy(*triad,word_to_vec_map)))
italy -> italian <====> spain -> spanish
india -> delhi <====> japan -> tokyo
man -> woman <====> boy -> girl
small -> smaller <====> large -> larger
You can change the words above at will,See if you can get the desired output,You can also try if you can make the program make a little mistake.?比如:small -> smaller <===> big -> ? ,try it yourself~
triads_to_try = [('small', 'smaller', 'big')]
for triad in triads_to_try:
print ('{} -> {} <====> {} -> {}'.format( *triad, complete_analogy(*triad,word_to_vec_map)))
small -> smaller <====> big -> competitors
The following are key points you should remember:
在下面的練習中,You will study embeddable word embedded gender bias,And explore the algorithm reduce prejudice.In addition to understanding the subject of deskewing,This exercise will also help you sharpen your intuition,Understand what word vectors are doing.This section involves some linear algebra,Although even if you are not good at linear algebra,you can also do it,We encourage you to try it.
首先讓我們看看GloVeThe relationship between word embeddings and gender.you will first calculate the vector g = e w o m a n − e m a n g = e_{woman}-e_{man} g=ewoman−eman,其中 e w o m a n e_{woman} ewomanmeans with wordswoman對應的單詞向量,而 e m a n e_{man} emanthen corresponds to the word corresponding to the wordman對應的向量.resulting vector g g gGeneral coding“性別”的概念.(如果你計算 g 1 = e m o t h e r − e f a t h e r g_1 = e_{mother}-e_{father} g1=emother−efather, g 2 = e g i r l − e b o y g_2 = e_{girl}-e_{boy} g2=egirl−eboy等,並對其進行平均,may result in a more accurate representation.但是僅使用 e w o m a n − e m a n e_{woman}-e_{man} ewoman−emanwill give you good enough results.)
g = word_to_vec_map['woman'] - word_to_vec_map['man']
print(g)
[-0.087144 0.2182 -0.40986 -0.03922 -0.1032 0.94165
-0.06042 0.32988 0.46144 -0.35962 0.31102 -0.86824
0.96006 0.01073 0.24337 0.08193 -1.02722 -0.21122
0.695044 -0.00222 0.29106 0.5053 -0.099454 0.40445
0.30181 0.1355 -0.0606 -0.07131 -0.19245 -0.06115
-0.3204 0.07165 -0.13337 -0.25068714 -0.14293 -0.224957
-0.149 0.048882 0.12191 -0.27362 -0.165476 -0.20426
0.54376 -0.271425 -0.10245 -0.32108 0.2516 -0.33455
-0.04371 0.01258 ]
現在,you will consider different words g g g的余弦相似度.Consider what a positive value of similarity means vs a negative value of cosine similarity.
print ('List of names and their similarities with constructed vector:')
# girls and boys name
name_list = ['john', 'marie', 'sophie', 'ronaldo', 'priya', 'rahul', 'danielle', 'reza', 'katy', 'yasmin']
for w in name_list:
print (w, cosine_similarity(word_to_vec_map[w], g))
List of names and their similarities with constructed vector:
john -0.23163356145973724
marie 0.315597935396073
sophie 0.31868789859418784
ronaldo -0.31244796850329437
priya 0.17632041839009402
rahul -0.16915471039231716
danielle 0.24393299216283895
reza -0.07930429672199553
katy 0.2831068659572615
yasmin 0.23313857767928758
如你所見,Women's name and we construct vector g g gThe cosine similarity of is positive,while male names have a negative similarity to cosine.這並不令人驚訝,結果似乎可以接受.
但是,Let's try some other words.
print('Other words and their similarities:')
word_list = ['lipstick', 'guns', 'science', 'arts', 'literature', 'warrior','doctor', 'tree', 'receptionist',
'technology', 'fashion', 'teacher', 'engineer', 'pilot', 'computer', 'singer']
for w in word_list:
print (w, cosine_similarity(word_to_vec_map[w], g))
Other words and their similarities:
lipstick 0.2769191625638267
guns -0.1888485567898898
science -0.06082906540929701
arts 0.008189312385880337
literature 0.06472504433459932
warrior -0.20920164641125288
doctor 0.11895289410935041
tree -0.07089399175478091
receptionist 0.33077941750593737
technology -0.13193732447554302
fashion 0.03563894625772699
teacher 0.17920923431825664
engineer -0.0803928049452407
pilot 0.0010764498991916937
computer -0.10330358873850498
singer 0.1850051813649629
Are you surprised??令人驚訝的是,How these results reflect some unhealthy gender stereotypes.例如,“computer"更接近 “man”,而"literature” 更接近"woman".
We will see below how to useBoliukbasi et al., 2016proposed algorithm to reduce the bias of these vectors.注意,諸如 “actor”/“actress” 或者 “grandmother”/“grandfather"Word correspondences such as remain gender specific,而諸如"receptionist” 或者"technology"Other words like should be neutralized,regardless of gender.when eliminating prejudice,You will have to treat the two types of words differently.
The diagram below should help you visualize what neutralization does.如果你使用的是50維詞嵌入,則50The dimensional space can be divided into two parts:偏移方向 g g g和其余49維,我們將其稱為 g ⊥ g_{\perp} g⊥.在線性代數中,我們說49維 g ⊥ g_{\perp} g⊥與 g g g垂直(或“正交”),這意味著它與 g g g成90度.The neutralization step takes a vector,例如 e r e c e p t i o n i s t e_{receptionist} ereceptionist,並沿 g g gdirection to clear the component to zero,從而得到 e r e c e p t i o n i s t d e b i a s e d e_{receptionist}^{debiased} ereceptionistdebiased.
即使 g ⊥ g_{\perp} g⊥是49維的,Given the limitations of what we can draw on the screen,我們還是使用下面的1dimension axis to explain it.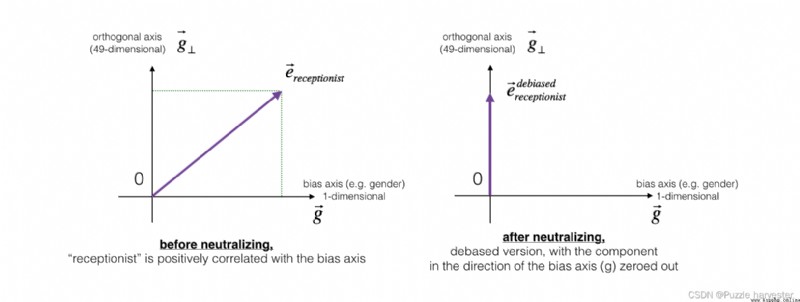
圖2:In the application and before and after the operation,代表"receptionist"的單詞向量.
練習:實現neutralize()to eliminate such as"receptionist" 或 "scientist"words like prejudice.given embedding e e e的輸入,You can use the following formula to calculate e d e b i a s e d e^{debiased} edebiased:
e b i a s _ c o m p o n e n t = e ⋅ g ∣ ∣ g ∣ ∣ 2 2 ∗ g (2) e^{bias\_component} = \frac{e \cdot g}{||g||_2^2} * g\tag{2} ebias_component=∣∣g∣∣22e⋅g∗g(2)
e d e b i a s e d = e − e b i a s _ c o m p o n e n t (3) e^{debiased} = e - e^{bias\_component}\tag{3} edebiased=e−ebias_component(3)
If you are an expert in linear algebra,則可以將 e b i a s _ c o m p o n e n t e^{bias\_component} ebias_component識別為 e e e在 g g g方向上的投影.If you are not an expert in the linear algebra,請不必為此擔心.
提醒:向量 u u u可分為兩部分:on the vector axis v B v_B vBprojection on and on with v v vProjection on Orthogonal Axis:
u = u B + u ⊥ u = u_B + u_{\perp} u=uB+u⊥
其中: u B = u_B= uB= and u ⊥ = u − u B u_{\perp} =u - u_B u⊥=u−uB
def neutralize(word, g, word_to_vec_map):
""" 通過將“word”Project onto space orthogonal to the offset axis,消除了“word”的偏差. 該函數確保“word”The values in the subspace of the sexes0 參數: word -- String to be debiased g -- 維度為(50,),corresponds to the offset axis(如性別) word_to_vec_map -- 字典類型,單詞到GloVe向量的映射 返回: e_debiased -- vector with bias removed. """
# 根據wordSelect the corresponding word vector
e = word_to_vec_map[word]
# 根據公式2計算e_biascomponent
e_biascomponent = np.divide(np.dot(e, g), np.square(np.linalg.norm(g))) * g
# 根據公式3計算e_debiased
e_debiased = e - e_biascomponent
return e_debiased
e = "receptionist"
print("Before going to the deviation{0}與g的余弦相似度為:{1}".format(e, cosine_similarity(word_to_vec_map["receptionist"], g)))
e_debiased = neutralize("receptionist", g, word_to_vec_map)
print("After debiasing{0}與g的余弦相似度為:{1}".format(e, cosine_similarity(e_debiased, g)))
Before going to the deviationreceptionist與g的余弦相似度為:0.33077941750593737
After debiasingreceptionist與g的余弦相似度為:-2.099120994400013e-17
接下來,Let's see how the bias can also be applied to word pairs,例如"actress"和"actor".Equilibrium only application and you hope that through different words for gender attributes.as a concrete example,假設"actress"比"actor"更接近"babysit".By applying neutralization to"babysit",we can reduce with"babysit"Related to the gender stereotypes.但這仍然不能保證"actress"和"actor"與"babysit"等距,Equalization algorithm is responsible for this.
The key idea behind equilibrium is and ensure that a specific word49維 g ⊥ g_{\perp} g⊥等距.The equalization step also ensures that both equalization steps are now identical to e r e c e p t i o n i s t d e b i a s e d e_{receptionist}^{debiased} ereceptionistdebiasedor the same distance as any other neutralized work.The picture shows the balanced way of working: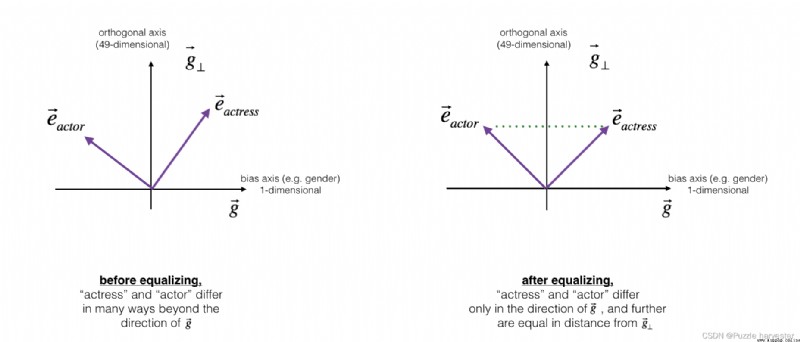
為此,The derivation of linear algebra is a bit more complicated.(詳細信息請參見Bolukbasi et al., 2016)But its key equation is:
μ = e w 1 + e w 2 2 (4) \mu = \frac{e_{w1} + e_{w2}}{2}\tag{4} μ=2ew1+ew2(4)
KaTeX parse error: Expected 'EOF', got '_' at position 39: …cdot \text{bias_̲axis}}{||\text{…
μ ⊥ = μ − μ B (6) \mu_{\perp} = \mu - \mu_{B} \tag{6} μ⊥=μ−μB(6)
KaTeX parse error: Expected 'EOF', got '_' at position 42: …cdot \text{bias_̲axis}}{||\text{…
KaTeX parse error: Expected 'EOF', got '_' at position 42: …cdot \text{bias_̲axis}}{||\text{…
e w 1 B c o r r e c t e d = ∣ 1 − ∣ ∣ μ ⊥ ∣ ∣ 2 2 ∣ ∗ e w1B − μ B ∣ ( e w 1 − μ ⊥ ) − μ B ) ∣ (9) e_{w1B}^{corrected} = \sqrt{ |{1 - ||\mu_{\perp} ||^2_2} |} * \frac{e_{\text{w1B}} - \mu_B} {|(e_{w1} - \mu_{\perp}) - \mu_B)|} \tag{9} ew1Bcorrected=∣1−∣∣μ⊥∣∣22∣∗∣(ew1−μ⊥)−μB)∣ew1B−μB(9)
e w 2 B c o r r e c t e d = ∣ 1 − ∣ ∣ μ ⊥ ∣ ∣ 2 2 ∣ ∗ e w2B − μ B ∣ ( e w 2 − μ ⊥ ) − μ B ) ∣ (10) e_{w2B}^{corrected} = \sqrt{ |{1 - ||\mu_{\perp} ||^2_2} |} * \frac{e_{\text{w2B}} - \mu_B} {|(e_{w2} - \mu_{\perp}) - \mu_B)|} \tag{10} ew2Bcorrected=∣1−∣∣μ⊥∣∣22∣∗∣(ew2−μ⊥)−μB)∣ew2B−μB(10)
e 1 = e w 1 B c o r r e c t e d + μ ⊥ (11) e_1 = e_{w1B}^{corrected} + \mu_{\perp} \tag{11} e1=ew1Bcorrected+μ⊥(11)
e 2 = e w 2 B c o r r e c t e d + μ ⊥ (12) e_2 = e_{w2B}^{corrected} + \mu_{\perp} \tag{12} e2=ew2Bcorrected+μ⊥(12)
練習:實現以下函數.Use the above equation to get the final equalized form of the word pair.
def equalize(pair, bias_axis, word_to_vec_map):
""" Eliminate gender bias by following the equalization approach described in the diagram above. 參數: pair -- Phrases to Eliminate Gender Bias,比如 ("actress", "actor") bias_axis -- 維度為(50,),corresponds to the offset axis(如性別) word_to_vec_map -- 字典類型,單詞到GloVe向量的映射 返回: e_1 -- word vector for the first word e_2 -- word vector for the second word """
# 第1步:獲取詞向量
w1, w2 = pair
e_w1, e_w2 = word_to_vec_map[w1], word_to_vec_map[w2]
# 第2步:計算w1與w2的均值
mu = (e_w1 + e_w2) / 2.0
# 第3步:計算muProjection on offset and orthogonal axes
mu_B = np.divide(np.dot(mu, bias_axis), np.square(np.linalg.norm(bias_axis))) * bias_axis
mu_orth = mu - mu_B
# 第4步:使用公式7、8計算e_w1B 與 e_w2B
e_w1B = np.divide(np.dot(e_w1, bias_axis), np.square(np.linalg.norm(bias_axis))) * bias_axis
e_w2B = np.divide(np.dot(e_w2, bias_axis), np.square(np.linalg.norm(bias_axis))) * bias_axis
# 第5步:根據公式9、10調整e_w1B 與 e_w2BThe offset part
corrected_e_w1B = np.sqrt(np.abs(1-np.square(np.linalg.norm(mu_orth)))) * np.divide(e_w1B-mu_B, np.abs(e_w1 - mu_orth - mu_B))
corrected_e_w2B = np.sqrt(np.abs(1-np.square(np.linalg.norm(mu_orth)))) * np.divide(e_w2B-mu_B, np.abs(e_w2 - mu_orth - mu_B))
# 第6步: 使e1和e2Is equal to the sum of the adjusted projection,從而消除偏差
e1 = corrected_e_w1B + mu_orth
e2 = corrected_e_w2B + mu_orth
return e1, e2
print("==========Before the isostatic correction==========")
print("cosine_similarity(word_to_vec_map[\"man\"], gender) = ", cosine_similarity(word_to_vec_map["man"], g))
print("cosine_similarity(word_to_vec_map[\"woman\"], gender) = ", cosine_similarity(word_to_vec_map["woman"], g))
e1, e2 = equalize(("man", "woman"), g, word_to_vec_map)
print("\n==========After the isostatic correction==========")
print("cosine_similarity(e1, gender) = ", cosine_similarity(e1, g))
print("cosine_similarity(e2, gender) = ", cosine_similarity(e2, g))
==========Before the isostatic correction==========
cosine_similarity(word_to_vec_map["man"], gender) = -0.11711095765336832
cosine_similarity(word_to_vec_map["woman"], gender) = 0.35666618846270376
==========After the isostatic correction==========
cosine_similarity(e1, gender) = -0.7165727525843935
cosine_similarity(e2, gender) = 0.7396596474928909
Feel free to use the word entered in the cell above,to apply equalization to other word pairs.
These debiasing algorithms are very helpful in reducing bias,但並不完美,and cannot remove all traces of deviation.例如,One disadvantage of this implementation is that only words are usedwoman和manto define the deviation direction g g g.如前所述,如果 g g g是通過計算 g 1 = e w o m a n − e m a n g_1 = e_{woman} - e_{man} g1=ewoman−eman; g 2 = e m o t h e r − e f a t h e r g_2 = e_{mother} - e_{father} g2=emother−efather; g 3 = e g i r l − e b o y g_3 = e_{girl} - e_{boy} g3=egirl−eboywait to define,then average them,可以更好地估計50dimensional word embedding space in“性別”維度.Also can use these variations.