文章目錄

• 一. 什麼是人工智能
• • 1.1 學習的能力，是智能的本質
  • 1.2 大數據時代，萬物互聯
  • 1.3 李世石 VS 阿法狗
• 二. 神經網絡概述
• • 2.1 人工智能 VS 深度學習
  • 2.2 述說圖片的故事
  • 2.3 無人駕駛汽車
  • 2.4 黑科技：Image Transfer
  • 2.5 圖像分類
  • • 2.5.1 挑戰: 照射角度
    • 2.5.2 挑戰:光照強度
    • 2.5.3 挑戰: 形狀改變
    • 2.5.4 挑戰: 部分遮蔽
    • 2.5.5 挑戰: 背景混入
  • 2.6 圖像分類常規套路
• 三. K近鄰
• • 3.1 K近鄰概述
  • 3.2 K 值的選擇
  • 3.3 數據庫樣例: CIFAR-10
  • 3.4 如何計算距離
  • 3.5 最近鄰代碼
  • 3.6 超參數
  • 3.7 K近鄰小結
• 四. 線性分類
• 五. 損失函數
• • 5.1 損失函數概述
  • 5.2 正則化
  • 5.3 損失函數終極版
• 六. Softmax 分類器
• • 6.1 Sigmoid函數
  • 6.2 Softmax 分類器概述
• 七. 最優化
• • 7.1 找到山坡的最低點
  • 7.2 梯度下降
  • 7.3 學習率
  • 7.4 反向傳播
• 八. 神經網絡
• • 8.1 神經網絡概述
  • 8.2 激活函數
  • 8.3 數據預處理
  • 8.4 DROP-OUT
• 參考：

一. 什麼是人工智能

1.1 學習的能力，是智能的本質

1.2 大數據時代，萬物互聯

其實人工智能誕生比較找，大數據時代的來臨，大大加速了人工智能的應用。

1.3 李世石 VS 阿法狗

4:1 李世石慘敗

二. 神經網絡概述

2.1 人工智能 VS 深度學習

隨著數據規模的增加，傳統人工智能算法的瓶頸就會出現，此時應該選擇深度學習算法。

2.2 述說圖片的故事

這些字幕是深度學習程序寫的

2.3 無人駕駛汽車

1. 物體檢測
2. 行人檢測
3. 標志識別
4. 速度識別
   …

2.4 黑科技：Image Transfer

Content + Style = Interesting thing

2.5 圖像分類

圖像分類是計算機視覺的核心任務。

假設我們有一系列的標簽：狗，貓，汽車，飛機。。。
我們怎麼才能判斷下面這張圖是貓呢?

一張圖片被表示成三維數組的形式，每個像素的值從0到255
例如：3001003
(最後的3代表顏色 RGB. R代表red，G代表Green，B代表Black)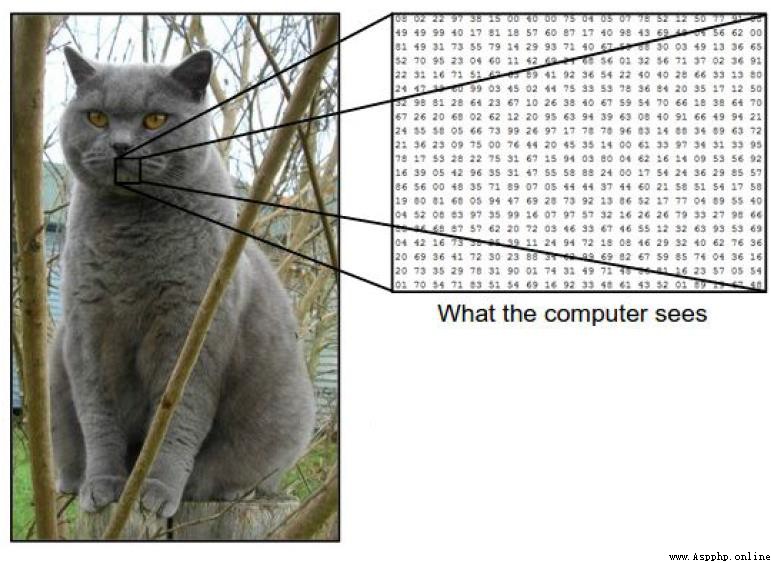

計算機視覺會存在很多干擾項。

2.5.1 挑戰: 照射角度

2.5.2 挑戰:光照強度

2.5.3 挑戰: 形狀改變

2.5.4 挑戰: 部分遮蔽

2.5.5 挑戰: 背景混入

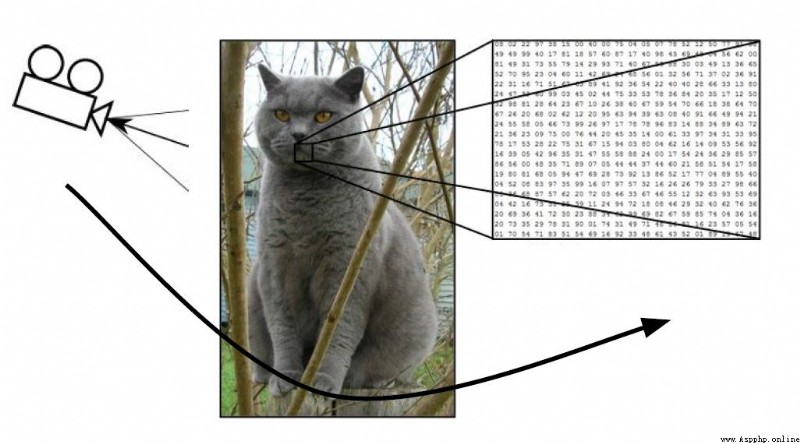
背景混入是目前最麻煩的一種情況

2.6 圖像分類常規套路

1. 收集數據並給定標簽
2. 訓練一個分類器
3. 測試，評估

三. K近鄰

3.1 K近鄰概述

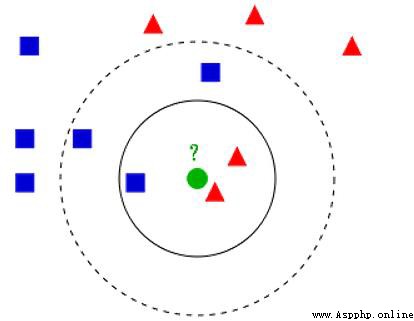
對於未知類別屬性數據集中的點：

1. 計算已知類別數據集中的點與當前點的距離
2. 按照距離依次排序
3. 選取與當前點距離最小的K個點
4. 確定前K個點所在類別的出現概率
5. 返回前K個點出現頻率最高的類別作為當前點預測分類。

概述：
KNN 算法本身簡單有效，它是一種lazy-learning 算法。
分類器不需要使用訓練集進行訓練，訓練時間復雜度為0。
KNN 分類的計算復雜度和訓練集中的文檔數目成正比，也就是說，如果訓練集中文檔總數為n，那麼KNN 的分類時間復雜度為O(n)。

3.2 K 值的選擇

距離度量和分類決策規則是該算法的三個基本要素

問題：
該算法在分類時有個主要的不足是，當樣本不平衡時，如一個類的樣本容量很大，而其他類樣本容量很小時，有可能導致當輸入一個新樣本時，該樣本的K 個鄰居中大容量類的樣本占多數

解決：
不同的樣本給予不同權重項

3.3 數據庫樣例: CIFAR-10

10類標簽
50000個訓練數據
10000個測試數據
大小均為32*32

3.4 如何計算距離

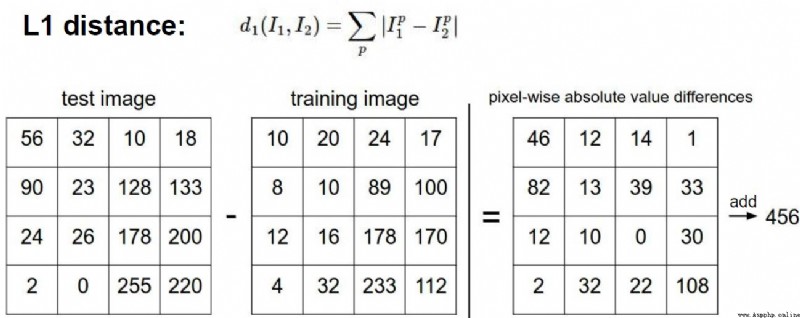
測試結果:
准確率較低

3.5 最近鄰代碼

3.6 超參數

3.7 K近鄰小結

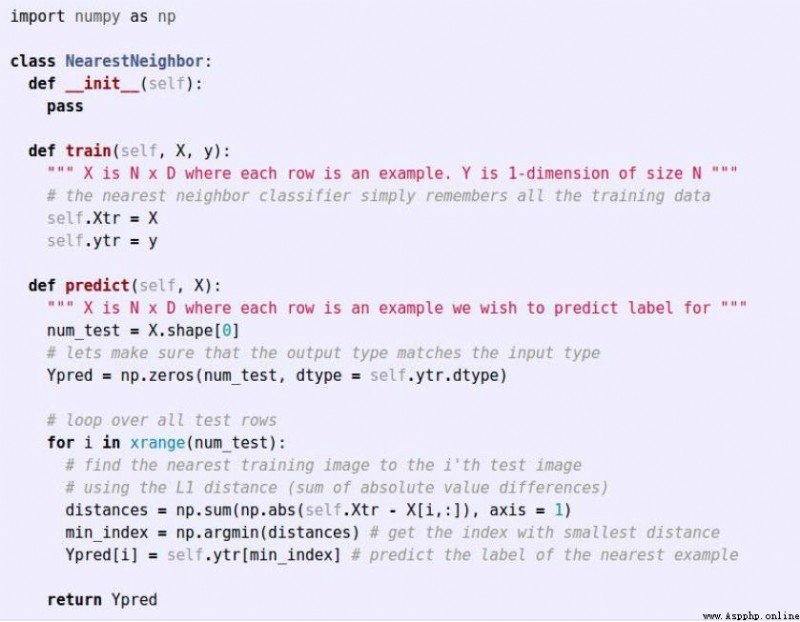
問題:

1. 對於距離如何設定？
2. 對於K近鄰的K該如何選擇？
3. 如果有的話，其它的超參數該怎麼設定呢？

交叉驗證: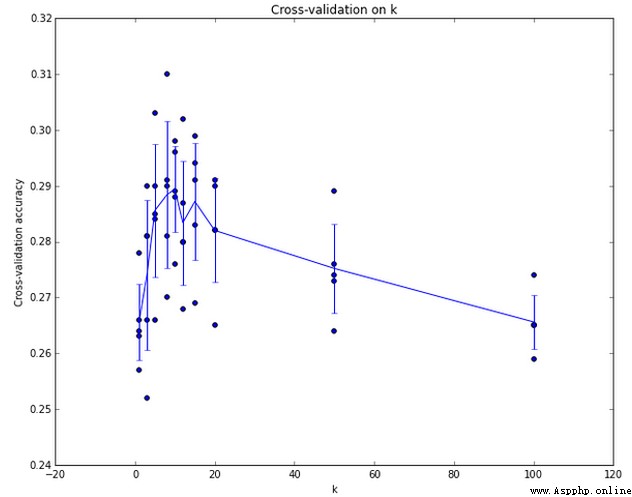

選取超參數的正確方法:

1. 選取超參數的正確方法是：將原始訓練集分為訓練集和驗證集，我們在驗證集上嘗試不同的超參數，最後保留表現最好那個。

2. 如果訓練數據量不夠，使用交叉驗證方法，它能幫助我們在選取最優超參數的時候減少噪音。

3. 一旦找到最優的超參數，就讓算法以該參數在測試集跑且只跑一次，並根據測試結果評價算法。

4. 最近鄰分類器能夠在CIFAR-10上得到將近40%的准確率。該算法簡單易實現，但需要存儲所有訓練數據，並且在測試的時候過於耗費計算能力。

5. 最後，我們知道了僅僅使用L1和L2范數來進行像素比較是不夠的，圖像更多的是按照背景和顏色被分類，而不是語義主體分身。

整體步驟:

1. 預處理你的數據：對你數據中的特征進行歸一化（normalize），讓其具有零平均值（zero mean）和單位方差（unit variance）。

2. 如果數據是高維數據，考慮使用降維方法，比如PCA。

3. 將數據隨機分入訓練集和驗證集。按照一般規律，70%-90% 數據作為訓練集。

4. 在驗證集上調優，嘗試足夠多的k值，嘗試L1和L2兩種范數計算方式。

四. 線性分類

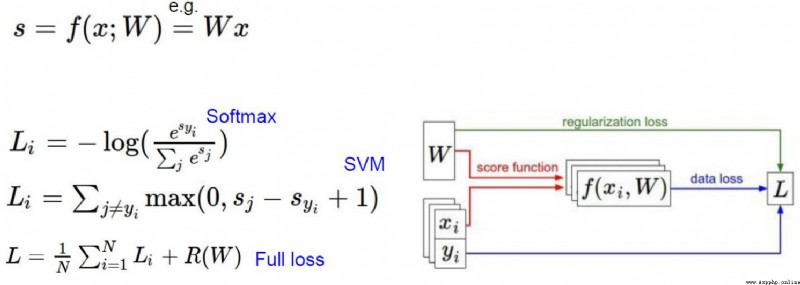
每個類別的得分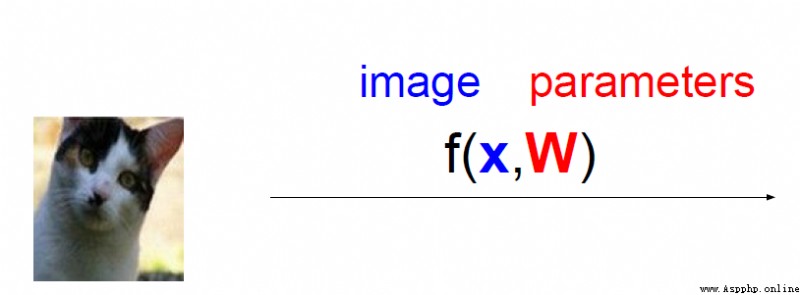

得分函數：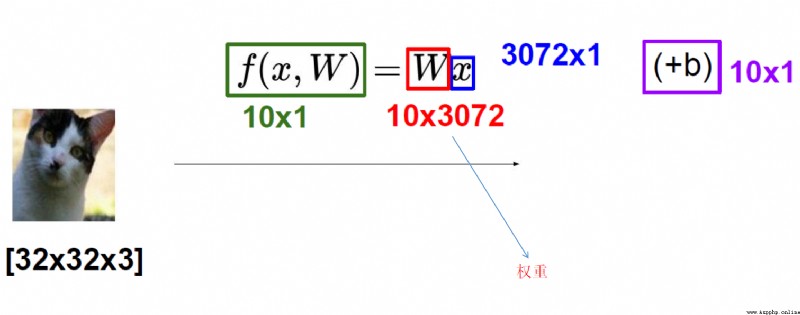

實例:
0.256 - 0.5231 + 0.124 + 2.02 + 1.1 = -96.8

五. 損失函數

5.1 損失函數概述

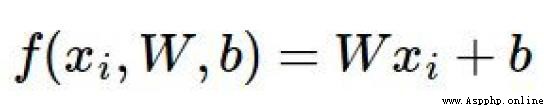
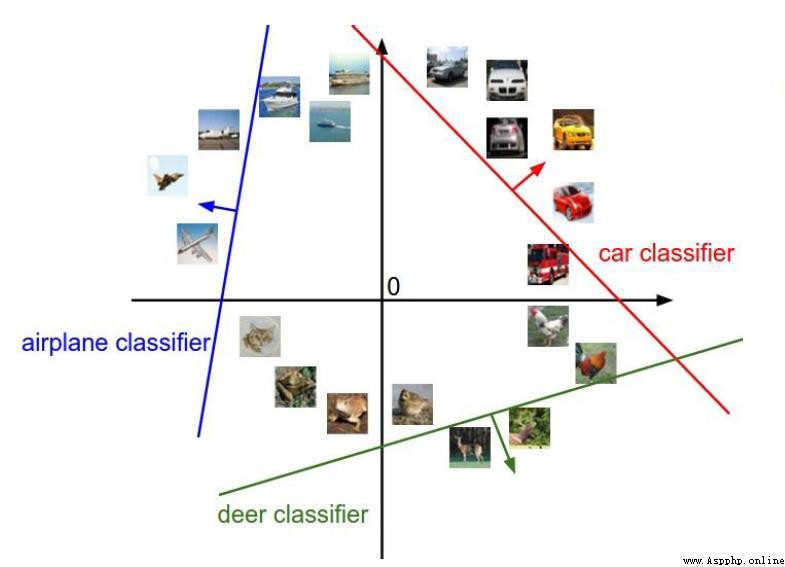
從上例可以看到，最終的評分效果不理想，預測值與實際值之間存在較大的差異，這個引入了損失函數。

從上圖可以看出，模型評估的效果越差的話，損失函數的值就越大。

損失函數: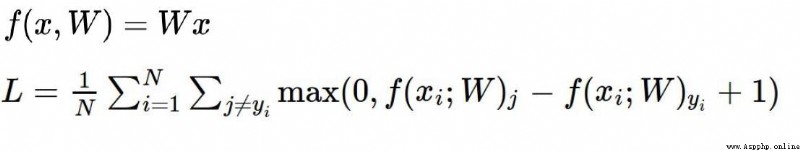

根據上圖的損失函數,結合下圖的x , w1, w2
會出現 f(x,w1) = f(x,w2)
但是w1只對一個變量設置了權重值，而w2卻對所有變量設置了權重值，雖然模型評分相同，但是理論上將更多的變量加入到模型中是更好的方法。

5.2 正則化

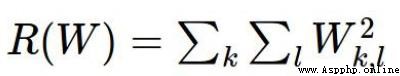
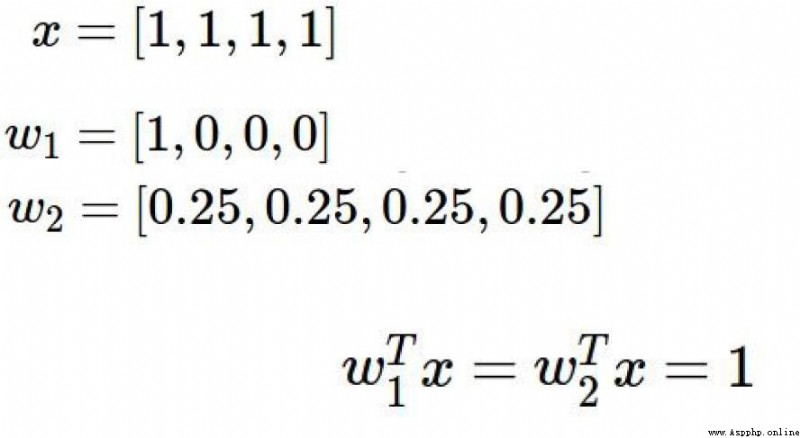
為了解決上面提出的問題，於是引入了正則化懲罰項
可以理解的理解 λ 就是 w 2 w^2 w2
y(x,w1) = 11 = 1
y(x,w2) = 0.250.25 + 0.250.25 + 0.250.25 + 0.25*0.25 = 0.25
此時y(x,w2) 的損失函數就小於y(x,w1),解決了上面的問題。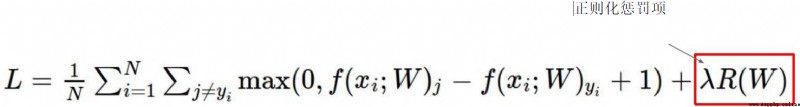

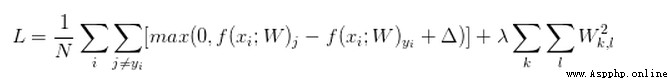
5.3 損失函數終極版

六. Softmax 分類器

Softmax 分類器 是 多類別分類，Softmax的輸出是概率。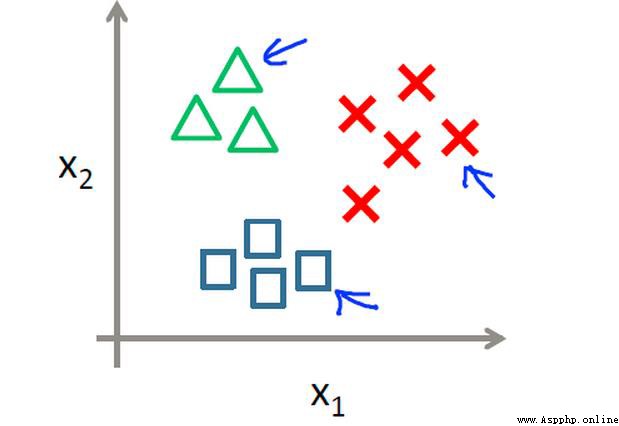

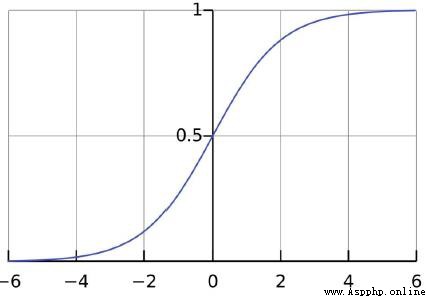
6.1 Sigmoid函數

Sigmoid是符號函數: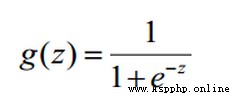

x取值范圍是(-∞,+∞),而y的取值范圍是[0-1]
剛好我們的概率取值范圍也是[0-1]，於是可以對應起來。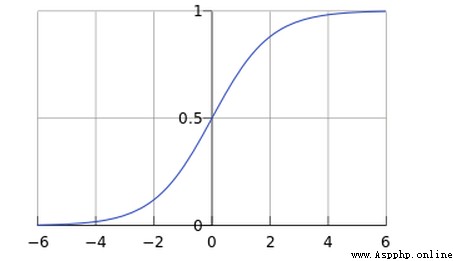

6.2 Softmax 分類器概述

Softmax的輸出（歸一化的分類概率）

損失函數：交叉熵損失（cross-entropy loss）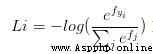

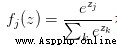
上圖被稱作softmax函數

其輸入值是一個向量，向量中元素為任意實數的評分值

輸出一個向量，其中每個元素值在0到1之間，且所有元素之和為1

七. 最優化

粗暴的想法: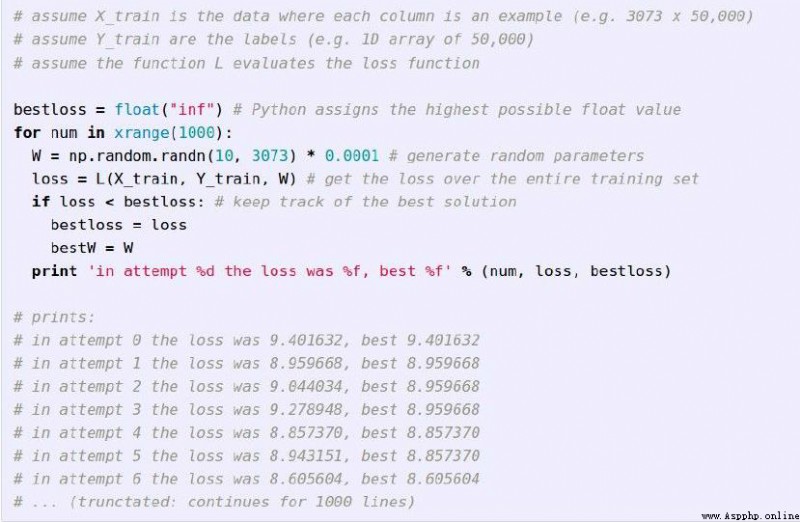

得到的結果: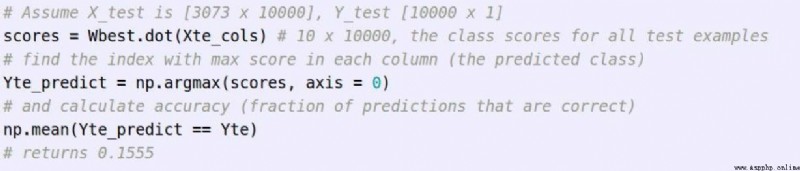

7.1 找到山坡的最低點

第一個位置是隨機的，然後不挺的迭代，找到最低點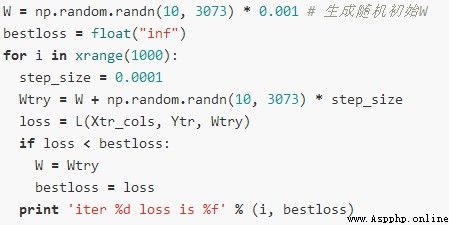

跟隨梯度:
[外鏈圖片轉存失敗,源站可能有防盜鏈機制,建議將圖片保存下來直接上傳(img-IYJswv5W-1659234249640)(https://upload-images.jianshu.io/upload_images/2638478-2962a7e9f53e5658.png?imageMogr2/auto-orient/strip%7CimageView2/2/w/1240)]

7.2 梯度下降

Bachsize通常是2的整數倍（32，64，128）

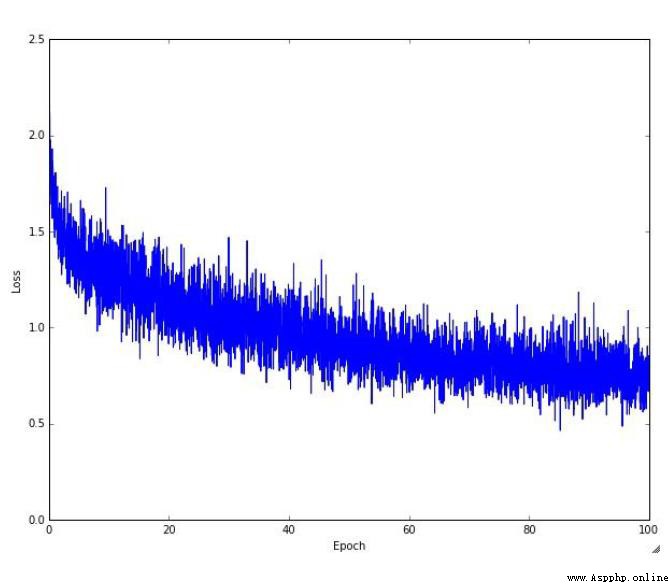
上圖是 訓練網絡時的LOSS值視化結果。

7.3 學習率

訓練網絡時的LOSS值視化結果

7.4 反向傳播

函數運行的結果與驗證集存在偏差(損失函數大)，此時可以通過反饋結果，調整權重參數，盡可能的將 損失函數的值變小。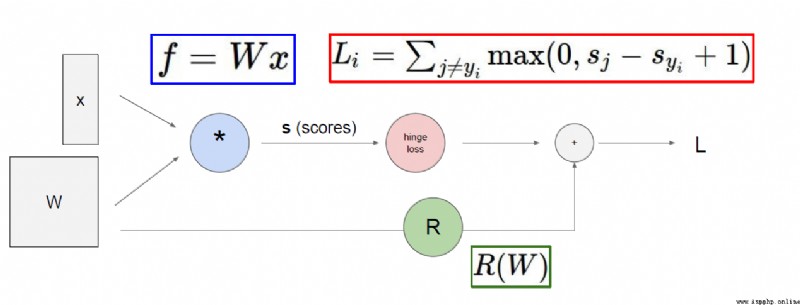

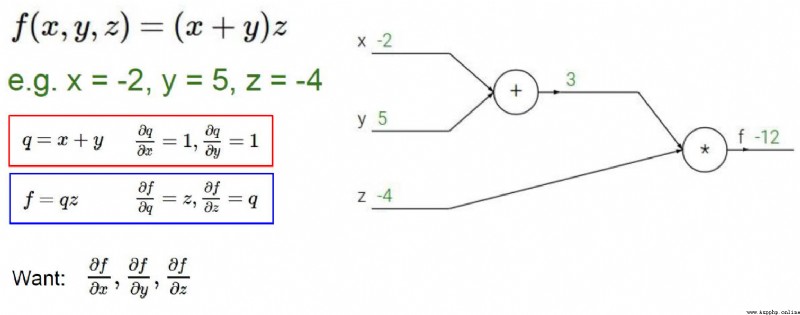
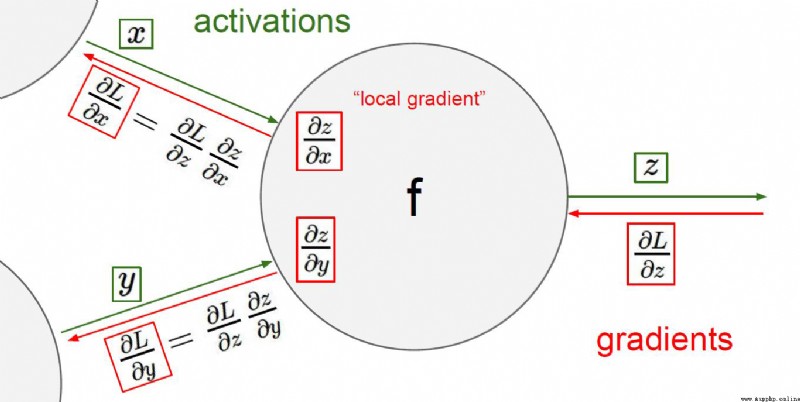
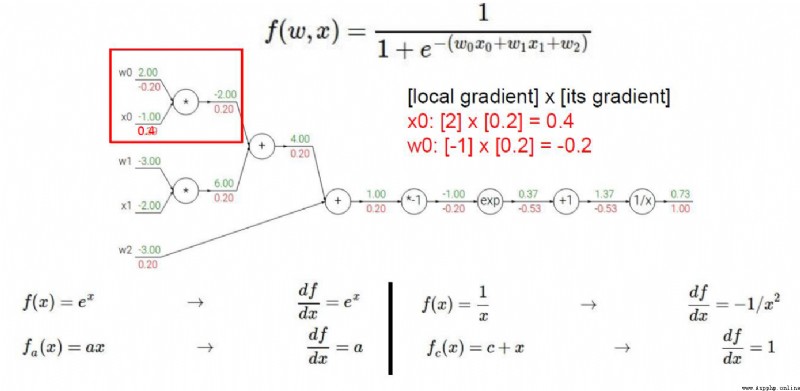
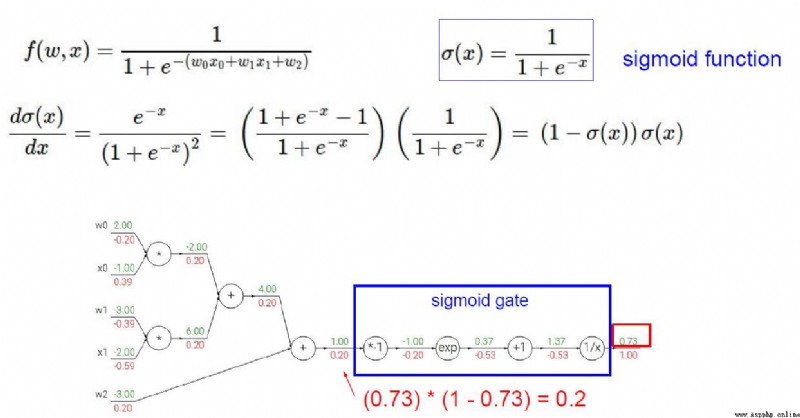
加法門單元：均等分配
MAX門單元：給最大的
乘法門單元：互換的感覺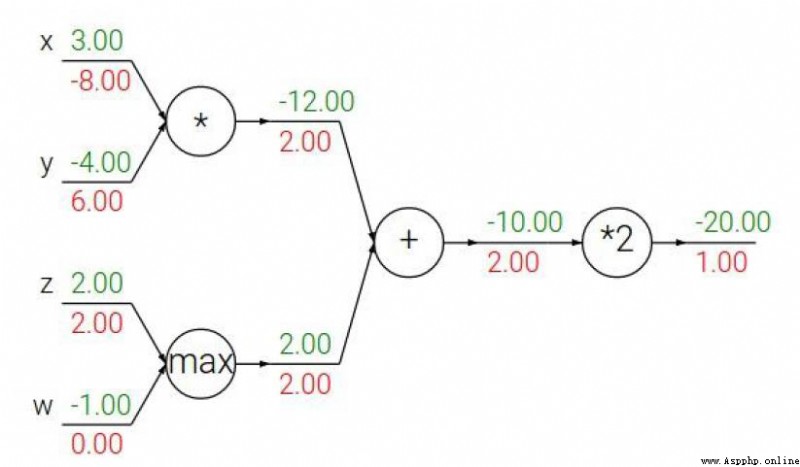

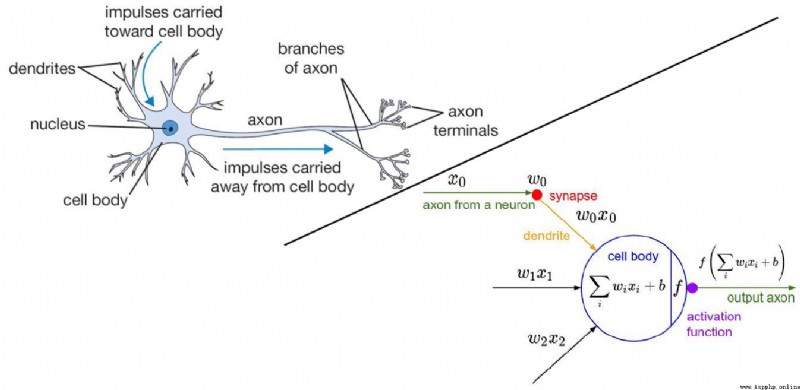
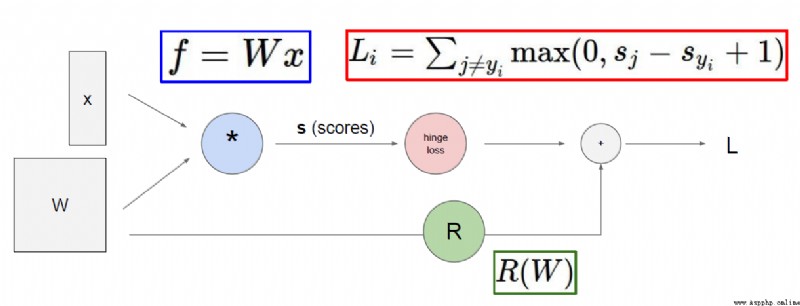
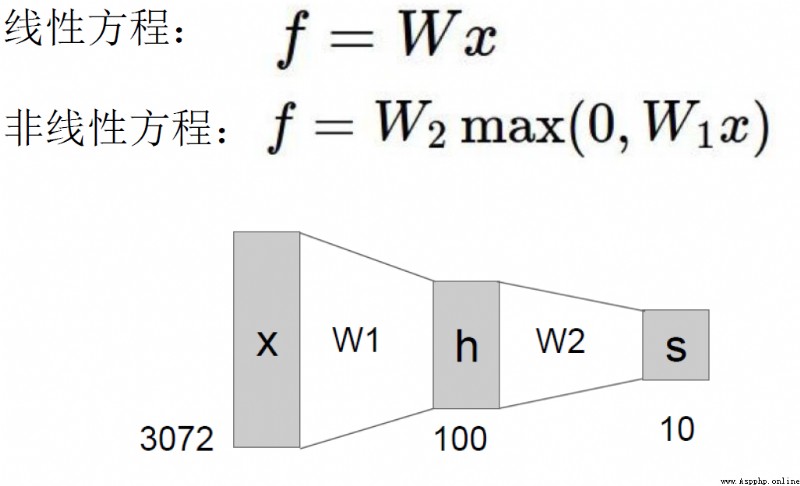
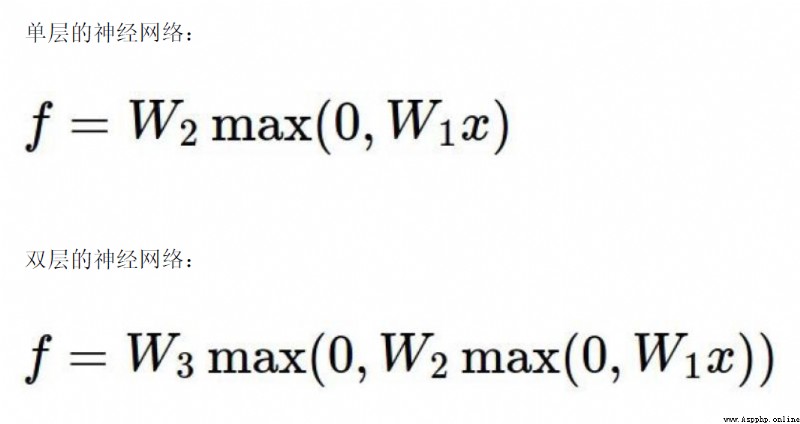
八. 神經網絡

8.1 神經網絡概述

正則化項在神經網絡中的重要作用

越多的神經元，就越能夠表達能復雜的模型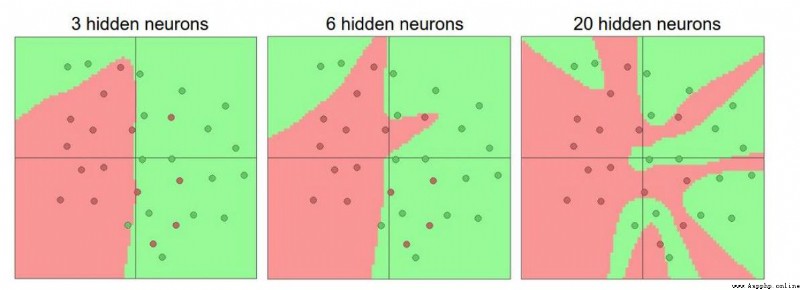

8.2 激活函數

激活函數是用來解決 預測結果與變量之間的非線性關系的問題。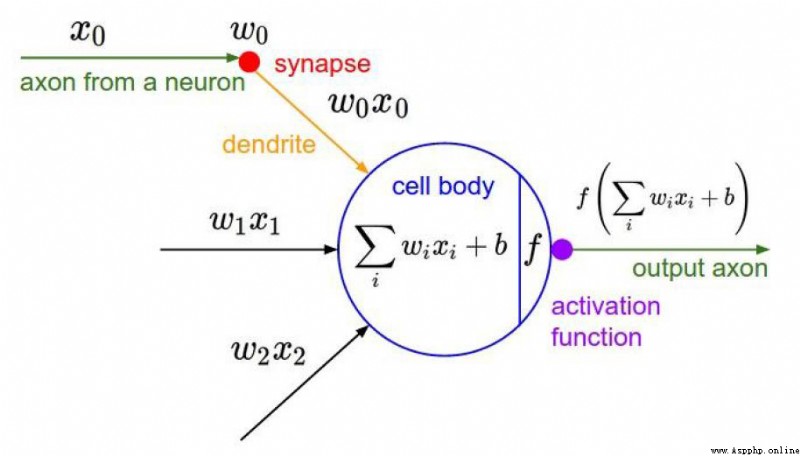

最開始的激活函數就是Sigmoid，但是他會存在一個梯度消失的問題。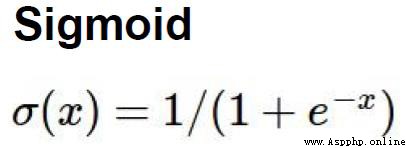

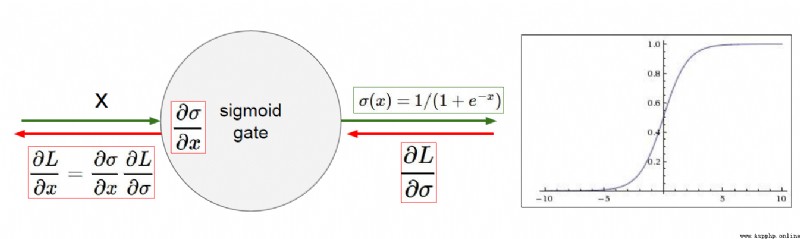
於是引入了新的激活函數ReLUctant
當x<=0的時候，y=0
當x > 0 的時候，y=x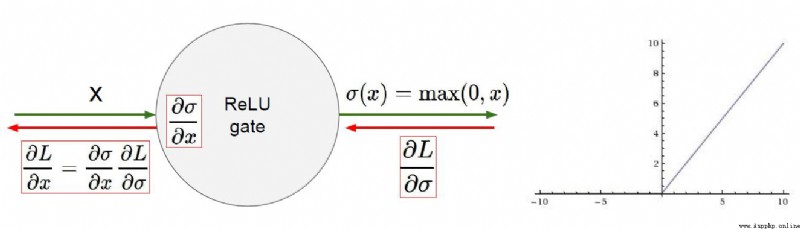

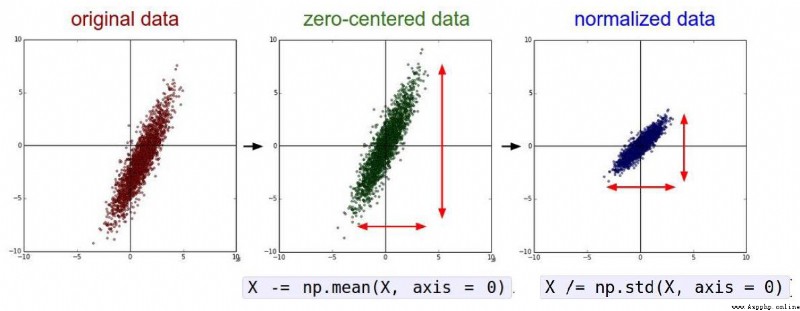
8.3 數據預處理

全零值初始化？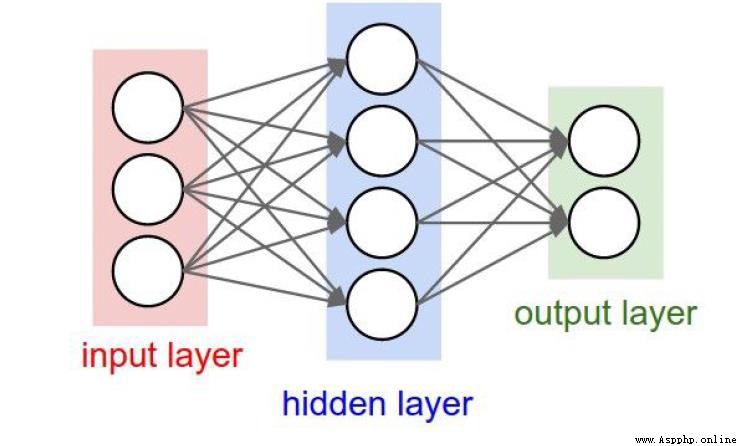

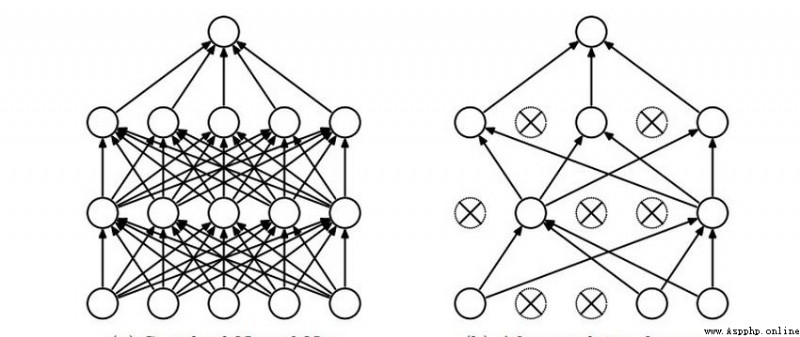
8.4 DROP-OUT

左圖是全連接，模型效果更優，但是模型也更復雜，計算量也大。
所以有了右圖的DROP-OUT，將一些不重要的連接去掉，保證模型效果的同時，盡量減少一些不必要的計算量。

參考：

1. https://study.163.com/course/introduction.htm?courseId=1003590004#/courseDetail?tab=1