掌握最小二乘法求解(無懲罰項的損失函數)、掌握加懲罰項(2 范數)的損失函數優化、梯度下降法、共轭梯度法、理解過擬合、克服過擬合的方法(如加懲罰項、增加樣本)
生成數據,加入噪聲;
用高階多項式函數擬合曲線;
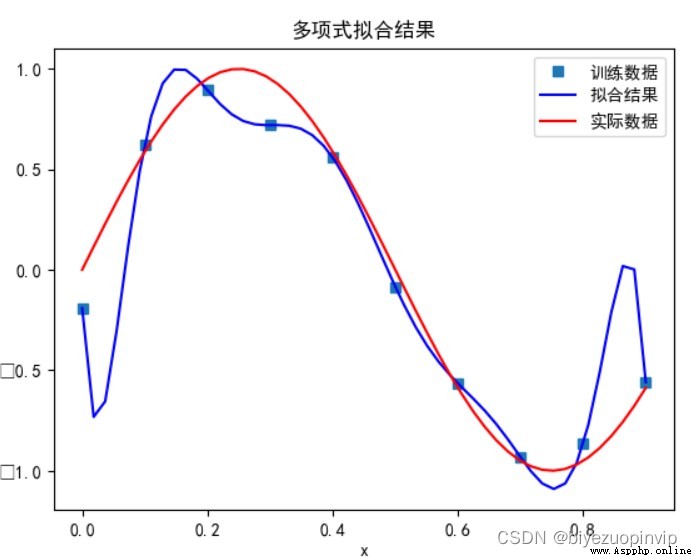
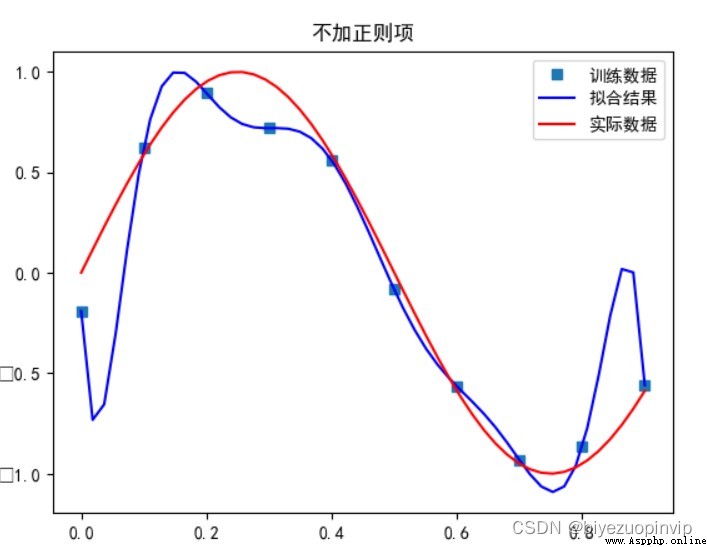
用解析解求解兩種 loss 的最優解(無正則項和有正則項)
優化方法求解最優解(梯度下降,共轭梯度);
用你得到的實驗數據,解釋過擬合。
用不同數據量,不同超參數,不同的多項式階數,比較實驗效果。
語言不限,可以用 matlab,python。求解解析解時可以利用現成的矩陣求逆。梯度下降,共轭梯度要求自己求梯度,迭代優化自己寫。不許用現成的平台,例如 pytorch,tensorflow 的自動微分工具。
本實驗需要用多項式來擬合正弦函數。在 m 階多項式中,有 m+1 個待定系數,m+1 個系數(由低到高)組成的(列)向量記作 w。要確定 w,用最小二乘法。
設 E(w) = 1/2 * (Xw – Y)^T(Xw – Y),其中,X 為多項式中各個未知項代入觀測數據求得的矩陣,若記 Xi 為 X 的第 i 行的向量,則 Xi[j]為第 i 個觀測數據 xi 的 j 次方,記有 n 組觀測數據,多項式最高次為 m,易知 X 的維度為 n * (m+1)。Y 為觀測標簽向量。即 Y[j]為第 j 組觀測數據的標簽值(即 y 值)。從而問題轉化為:求向量 w,使得 E(w)最小。
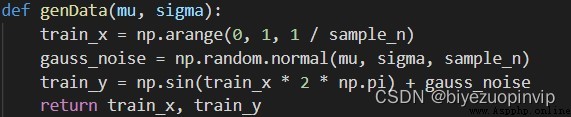

無正則項:
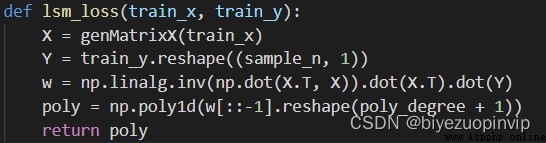
有正則項:

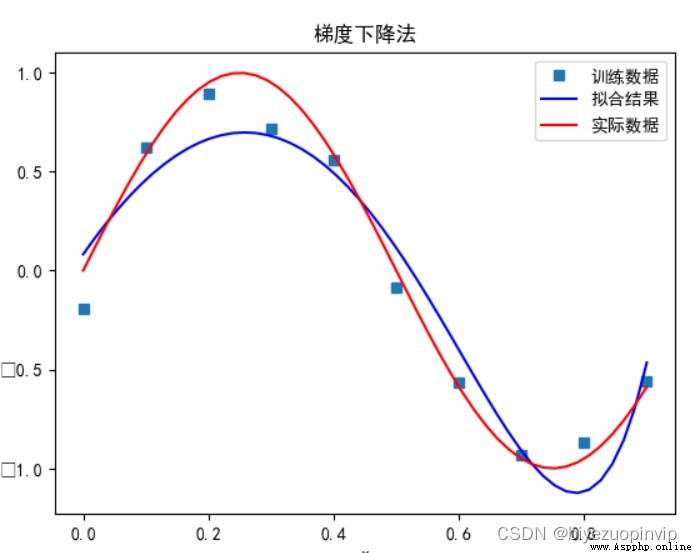
梯度下降法:
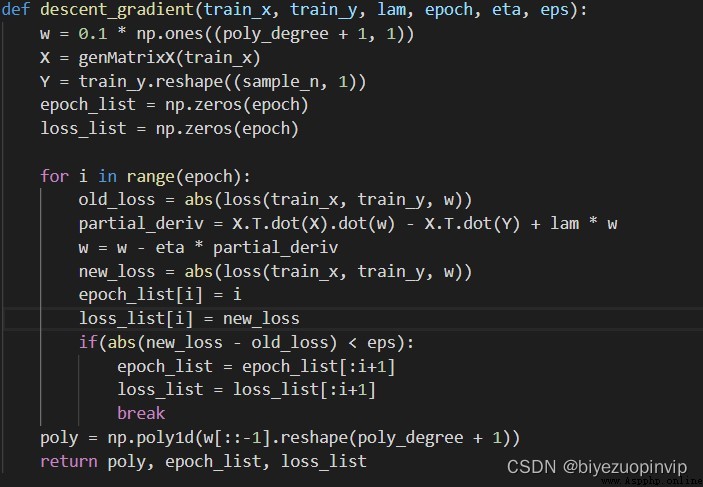
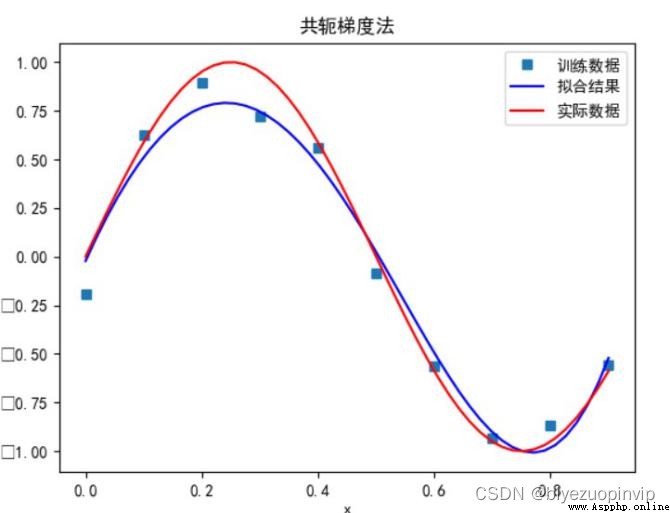
共轭梯度法:
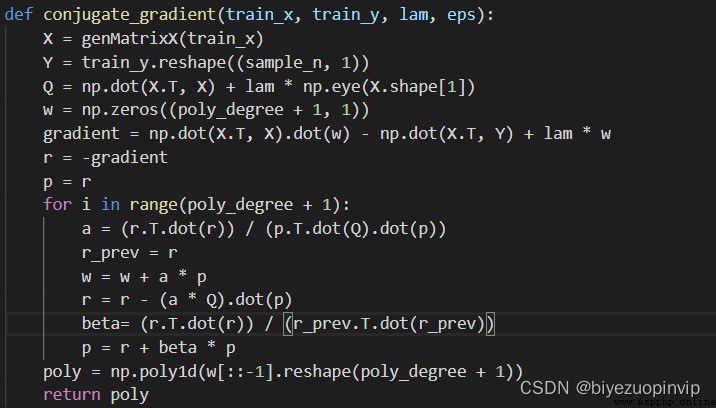
多項式次數為 1 時:
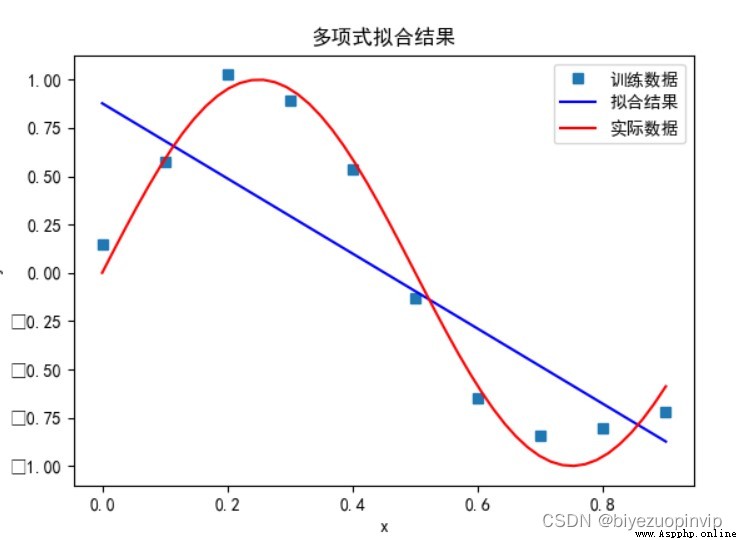
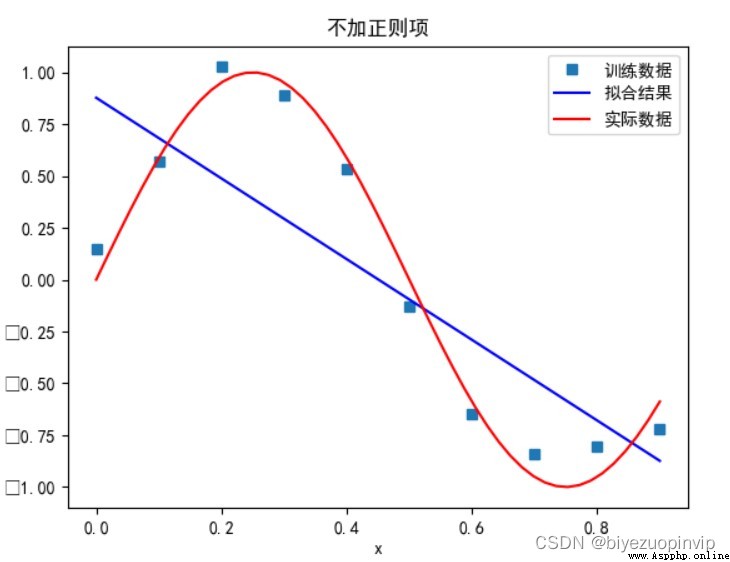
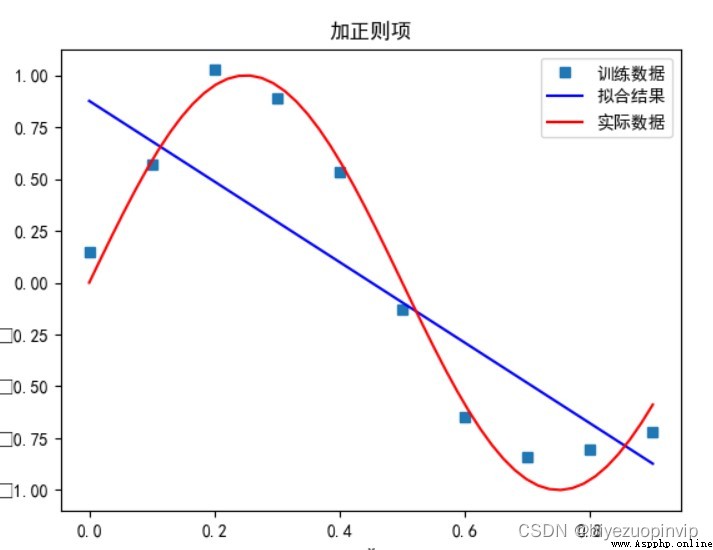
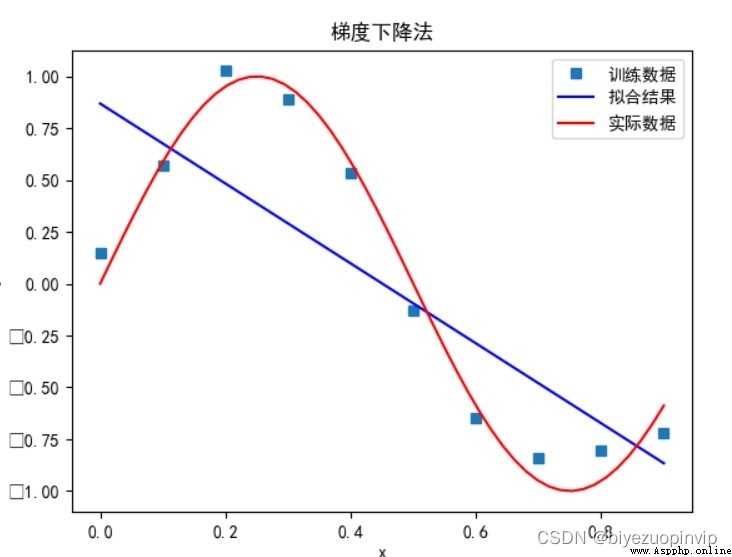
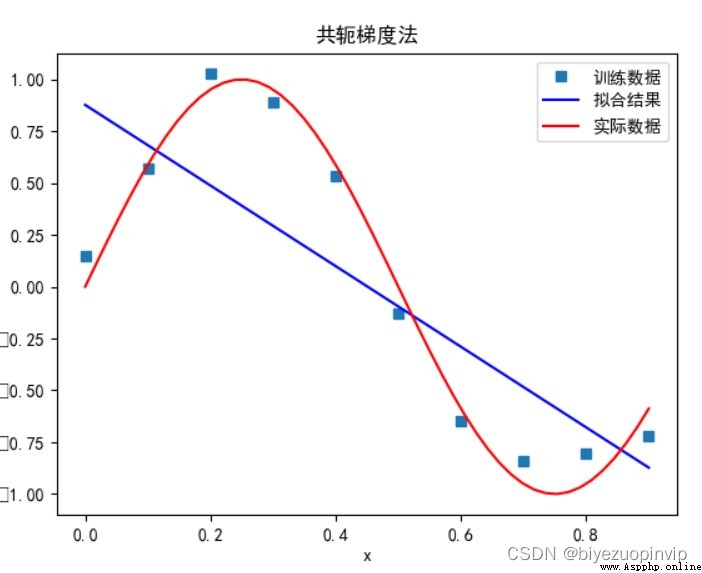
多項式次數為 3 時:
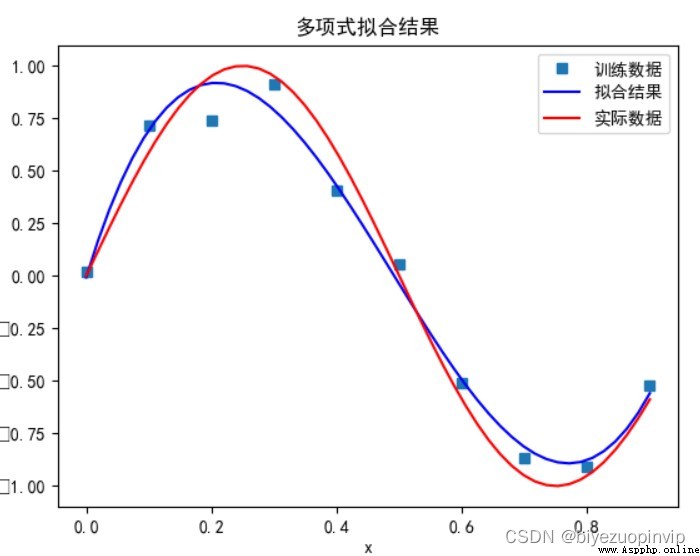
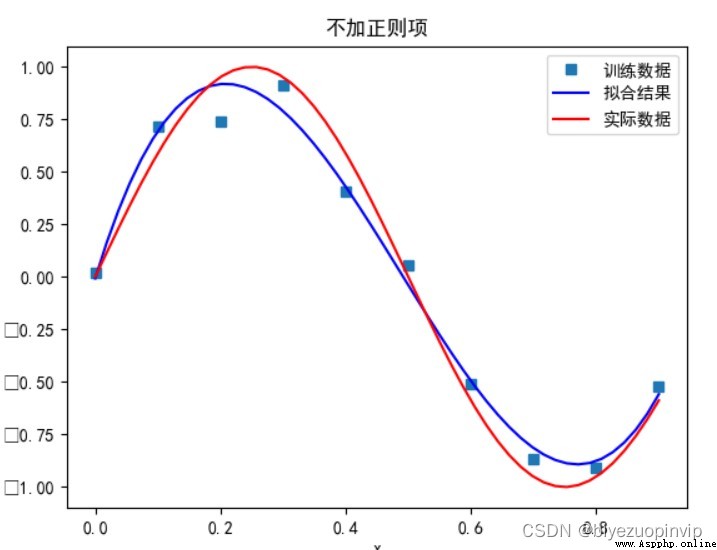
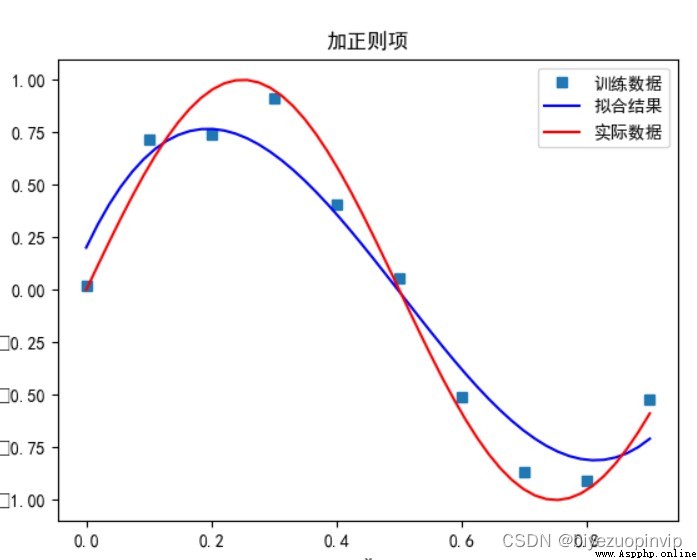
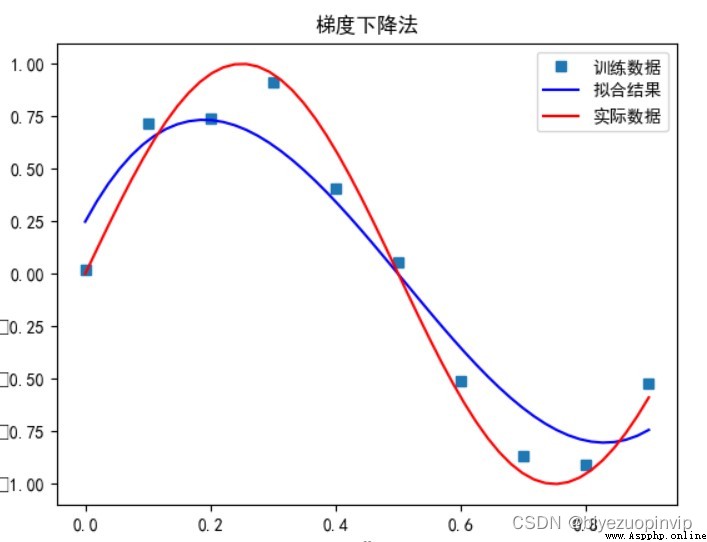
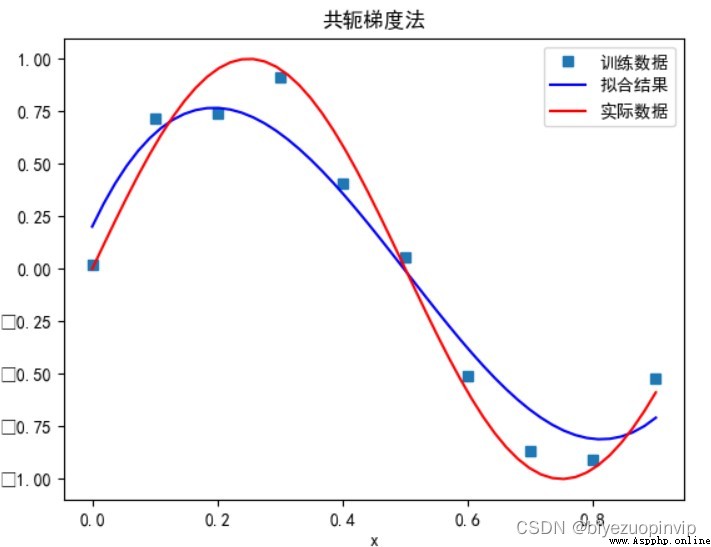
當多項式次數為 5 時: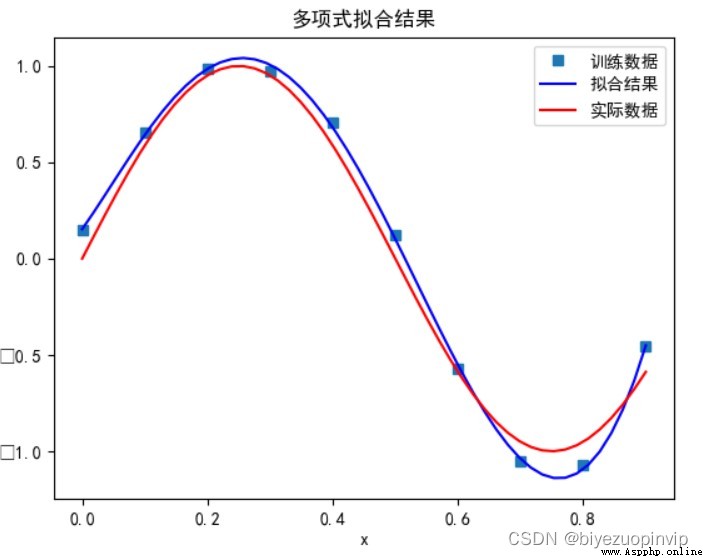
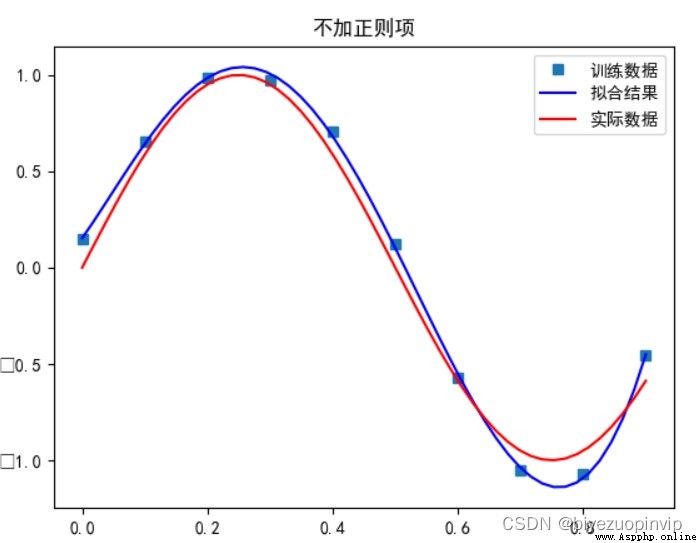
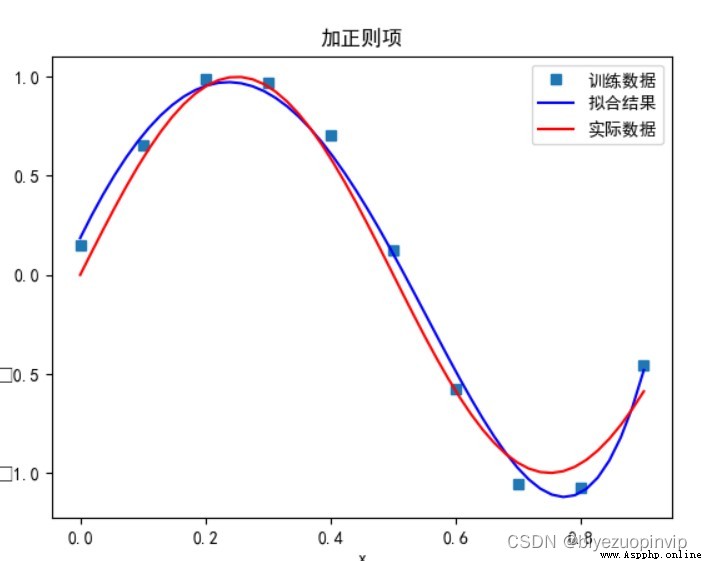
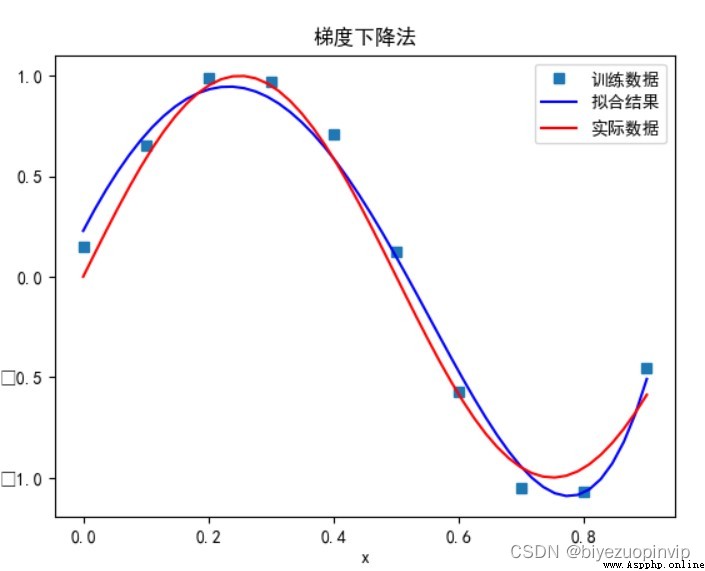
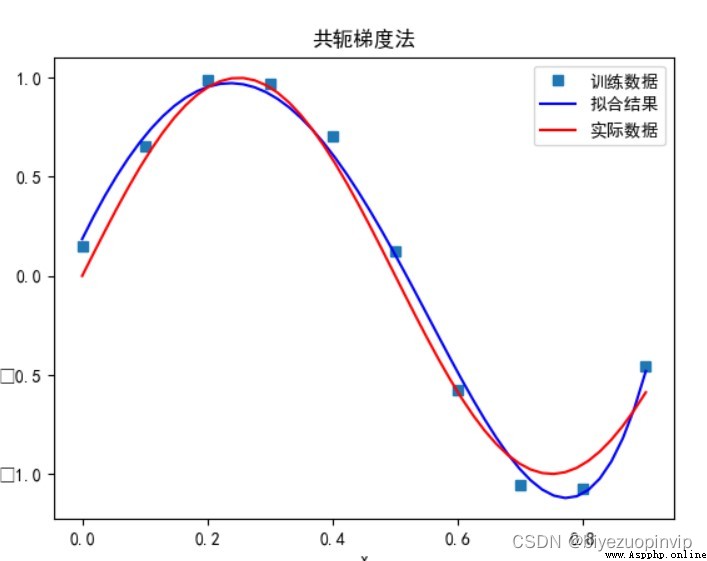
當多項式次數為 7 時:
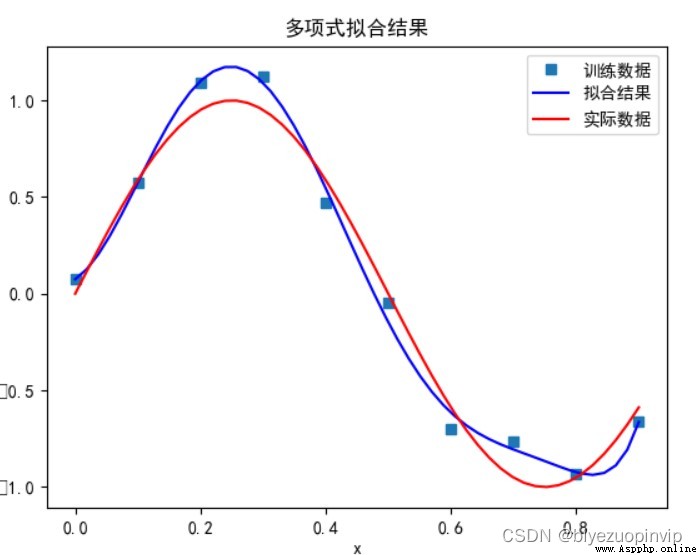
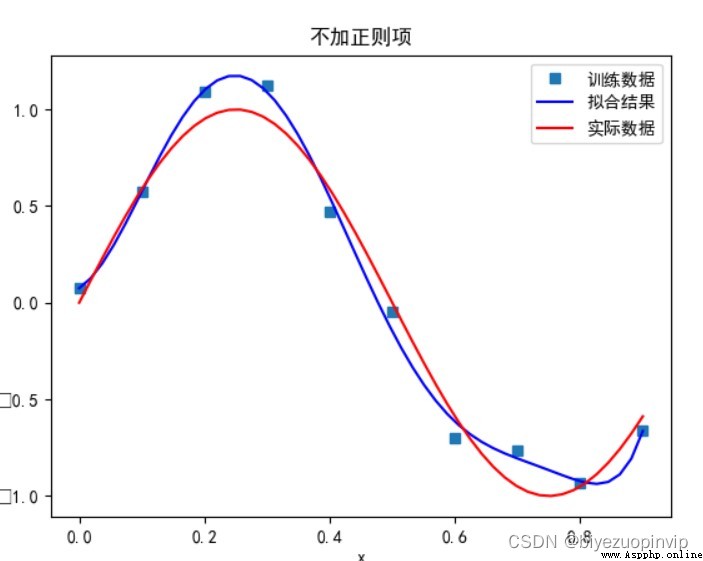
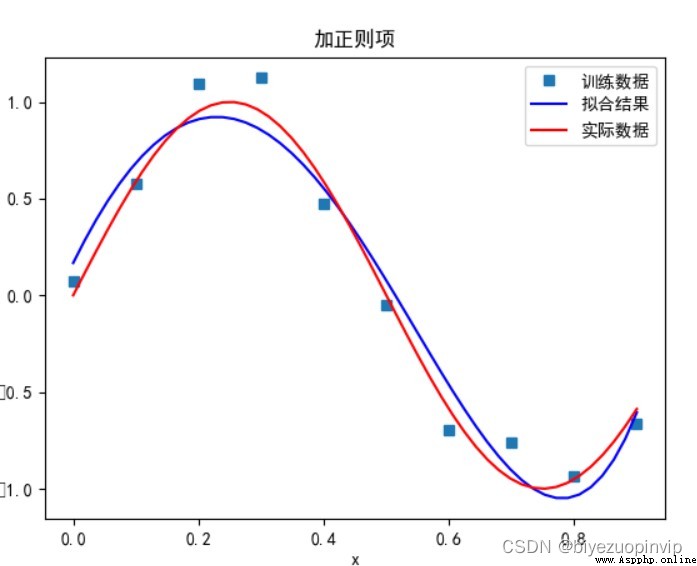
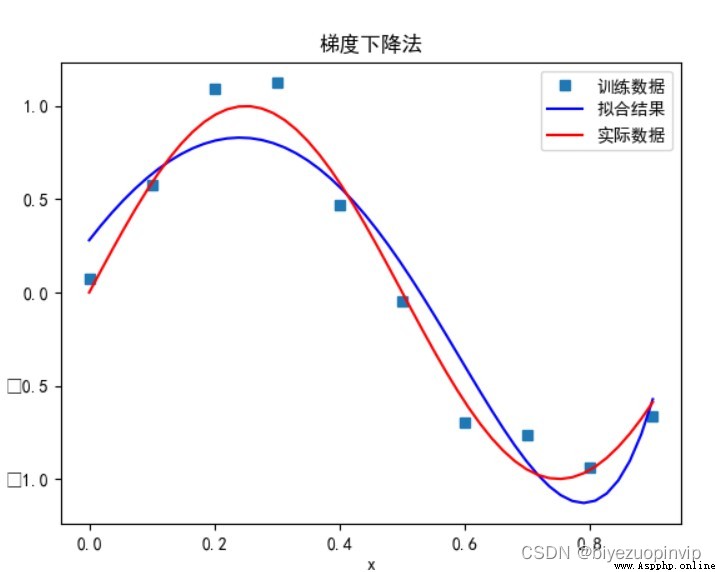
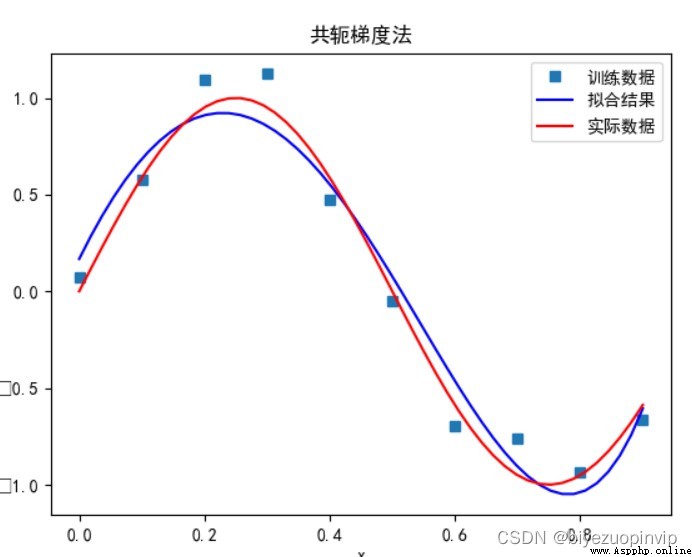
當多項式次數為 9 時: