numpy是python用於科學計算的基礎工具庫。它包含以下四大功能：

1. 強大的多維數組處理對象
2. 復雜的函數功能
3. 有用的線性代數，傅裡葉級數和隨機數功能
4. 集成C/C++和FORTRAN代碼的工具
   

   numpy庫的使用方法—Python

   • 一、 numpy的基本使用
   • • 1.函數的導入
     • 2.數組的創建
     • • 1.查看數據類型
       • 2.創建等差和等比數列
       • 3. 矩陣的生成
     • 3.數組元素的索引
   • 二、矩陣的合並與分割
   • • 1.矩陣的合並
     • 2.矩陣的分割
   • 三、矩陣的簡單運算
   • • 1.求和
     • 2.矩陣的逐個元素運算
   • 四、 矩陣運算與線性代數
   • • 1.范數的計算
     • 2.求解線性方程組
     • 3.求特征值和特征向量

一、 numpy的基本使用

1.函數的導入

import numpy as np

2.數組的創建

1.查看數據類型

import numpy as np
a1 = np.array([1, 2, 3, 4])#生成整數型數組
a2=a1.astype(float)#轉化為浮點數，此命令等於下面這個
a3=np.array([1, 2, 3, 4],dtype=float)#浮點數
#查看數據類型
a1.dtype
a2.dtype

一個是整數，一個是浮點數

2.創建等差和等比數列

等差數列：
arange(start,none,step,dtype) 分別是下限，上限，間隔，數字類型

np.arange(0,100,2)

linspace（statrt，stop，num，endpoint=T）分別是下限，上限，生成數字的個數，是否輸出最後一個數字

np.linspace(0,100,50,endpoint=False)

等比數列

np.logspace(0,10,num=20,dtype=int)

3. 矩陣的生成

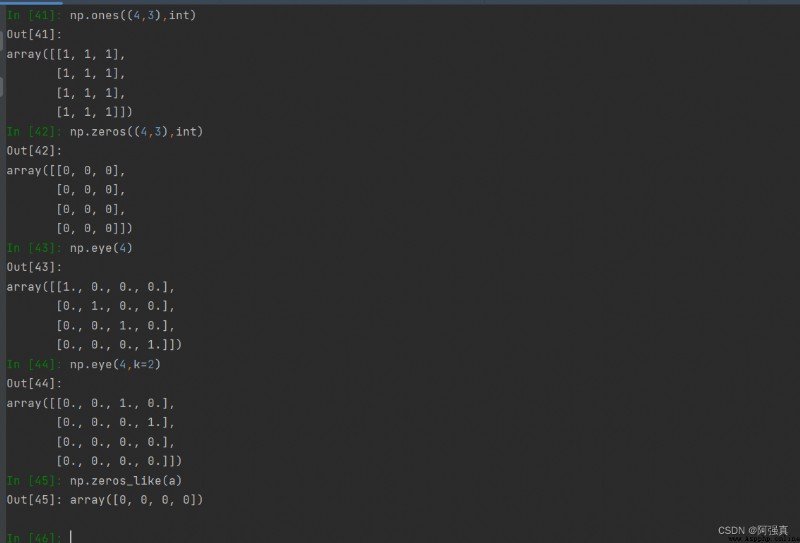
a=np.ones(4,int)#輸出[1, 1, 1, 1]
b=np.ones((4,3),int)#輸出四行三列的1
c=np.zeros((4,3),int)#輸出4行3列的0矩陣
d=np.eye(4)#生成4階單位陣
e=np.eye(4,k=2);e#輸出第k對角線元素為1,其他行元素為0的矩陣
f=np.zeros_like(a)#生成與a同維數的全0數組

3.數組元素的索引

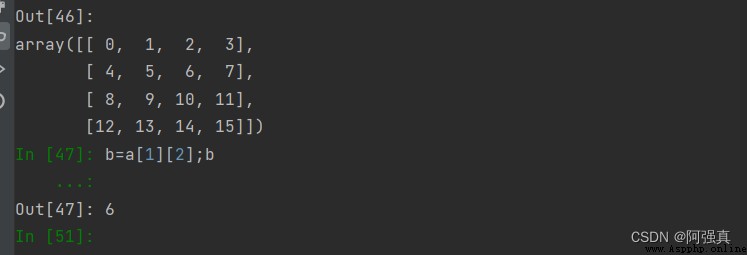
a=np.arange(16).reshape(4,4);a#生成四行四列的矩陣
b=a[1][2]#輸出第2行第3個，輸出6，此命令等於下面這個
c=a[1,2] #輸出結果也是6
x=np.array([0,1,2,1])
print(a[x==1])#輸出第2行和第四行

二、矩陣的合並與分割

1.矩陣的合並

import numpy as np
a=np.arange(16).reshape(4,4);a
b=np.floor(5*np.random.random((2,4)));b#生成一個2行4列在0到1上的隨機矩陣，乘以5,只保留整數部分
c=np.ceil(4*np.random.randint(4,7,(4,2)))#生成一個4行2列在4到7上的隨機整數矩陣，乘以4,ceil是向上取整函數
np.vstack([a,b])#上下合並矩陣，放在另外一個矩陣的下面
np.hstack([a,c])#左右和並矩陣

三個矩陣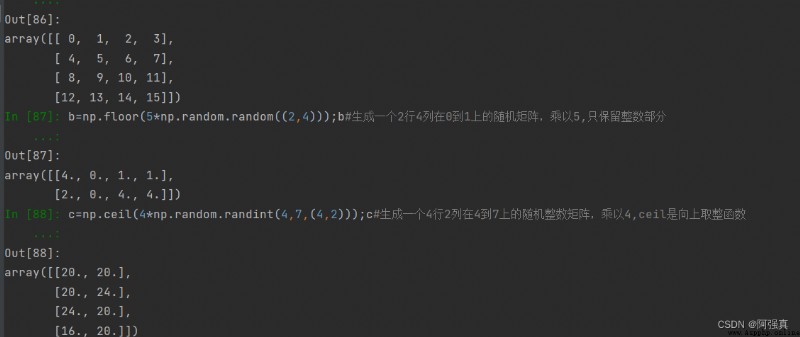

合並結果：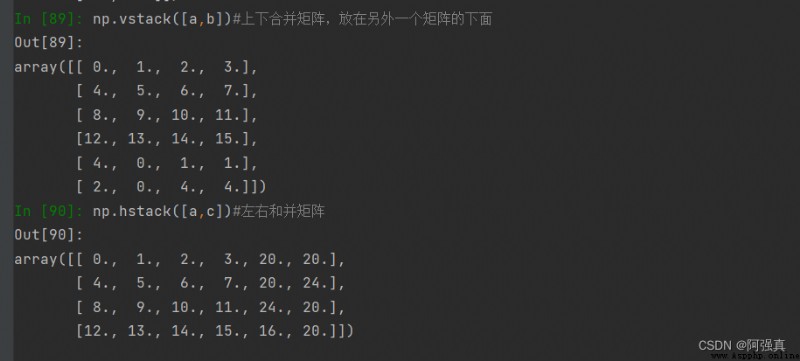

2.矩陣的分割

vsplit（a，m）把矩陣a平均分為m個行數組
hsplit（a，n）把矩陣a平均分為n個行數組

import numpy as np
a=np.arange(16).reshape(4,4)
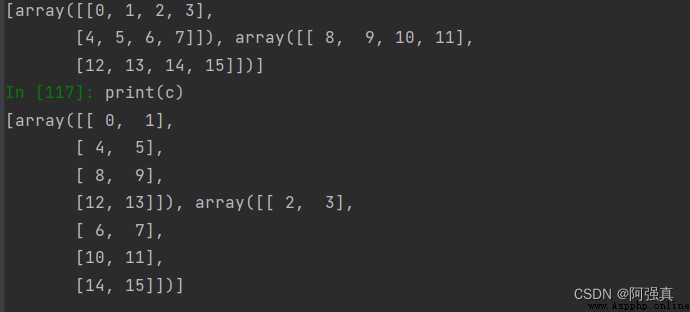
b=np.vsplit(a,2);b#分成兩個行數組
print(b)
c=np.hsplit(a,2)#分成兩個列數組
print(c)

三、矩陣的簡單運算

1.求和

import numpy as np
a=np.array([[1,2,3],[0,0,1],[1,2,1]])
a.sum()#求所有元素的和
sum(a)#求每一列元素的和,與下面兩個命令等價
np.sum(a,axis=0,keepdims=True)
np.sum(a,axis=0)
np.sum(a,axis=1)#逐行求和

2.矩陣的逐個元素運算

import numpy as np
a=np.array([[1,2,3],[0,0,1],[1,2,1]])
b=np.array([[1,2,3],[1,1,1],[1,2,1]])
a/b#兩個矩陣對應元素相除
a*b#兩個矩陣對應元素相乘
a+b#兩個矩陣對應元素相加
a-b#兩個矩陣對應元素相減
a**(1/2)#a矩陣所有元素都開根號

四、 矩陣運算與線性代數

1.范數的計算

定義：范數(norm)是數學中的一種基本概念。在泛函分析中，它定義在賦范線性空間中，並滿足一定的條件，即①非負性；②齊次性；③三角不等式。它常常被用來度量某個向量空間（或矩陣）中的每個向量的長度或大小。

例如：

向量 [ 1 , 2 , 3 ] T [1,2,3]^T [1,2,3]T的歐式范數(Euclidean norm) 為 1 2 + 2 2 + 3 2 = 13 \sqrt{1^2+2^2+3^2}=\sqrt{13} 12+22+32​=13​用於表示向量的大小，這個范數也被叫做 l 2 l_2 l2​ -范數。

為方便統一，一般將任意向量 x 的 l p l_p lp​-范數定義為:
∣ ∣ x ∣ ∣ = ∑ i ∣ x i ∣ p p \left| \left| x \right| \right|=\sqrt[p]{\sum_i{\left| x_i \right|^p}} ∣∣x∣∣=p​i∑​∣xi​∣p​

[參考文章](

import numpy as np
a=np.array([[0,3,4],[1,6,4]])
b=np.linalg.norm(a,axis=1)#行向量的2范數
c=np.linalg.norm(a,axis=0)#列向量的2范數
d=np.linalg.norm(a)#求矩陣的2范數
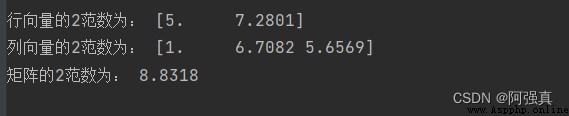
print("行向量的2范數為：",np.round(b,4))
print("列向量的2范數為：",np.round(c,4))
print("矩陣的2范數為：",np.round(d,4))

2.求解線性方程組

例1：
{ 3 x + y = 9 x + 2 y = 8 \begin{cases} 3x+y=9\\ x+2y=8\\ \end{cases} { 3x+y=9x+2y=8​
解法一：

根據 A X = B 可以求出 X = A − 1 B 於是我們可以先求出 A 的逆矩陣然後乘以 B \text{根據}AX=B\text{可以求出}X=A^{-1}B \\ \text{於是我們可以先求出}A\text{的逆矩陣然後乘以}B 根據AX=B可以求出X=A−1B於是我們可以先求出A的逆矩陣然後乘以B

import numpy as np
a=np.array([[3,1],[1,2]]);a
b=np.array([9,8]);b
np.linalg.inv(a)@b#@表示矩陣乘法

import numpy as np
a=np.array([[3,1],[1,2]]);a
b=np.array([9,8]);b
np.linalg.inv(a)@b#@表示矩陣乘法

方法二：直接根據np.linalg.solve函數來求

## 方法二：
np.linalg.solve(a,b)

求的結果都是X=2,Y=3
例2：
{ 3 x + y = 9 x + 2 y = 8 x + y = 6 \left\{ \begin{array}{c} \begin{array}{l} 3x+y=9\\ x+2y=8\\ \end{array}\\ x+y=6\\ \end{array} \right. ⎩⎨⎧​3x+y=9x+2y=8​x+y=6​

import numpy as np
a=np.array([[3,1],[1,2],[1,1]]);a
b=np.array([9,8,6]);b
c=np.linalg.pinv(a)@b#@表示矩陣乘法
print(np.round(c,2))

3.求特征值和特征向量

求下面矩陣的特征值和特征向量
∣ 0 0 0 1 0 1 1 0 0 1 0 0 1 0 0 0 ∣ \left| \begin{matrix} 0& 0& 0& 1\\ 0& 1& 1& 0\\ 0& 1& 0& 0\\ 1& 0& 0& 0\\ \end{matrix} \right| ∣∣​0001​0110​0100​1000​∣∣​

a=np.eye(4)
b=np.rot90(a)#將a矩陣順時針旋轉90度，得到我們將向的矩陣
c,d=np.linalg.eig(b)
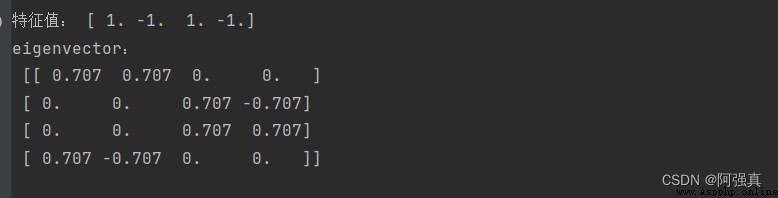
print("特征值：",c)
print("eigenvector：\n",np.round(d,3))

參考書籍