初步感受

我們先來初步實現一下階乘，也就是 n! = n*(n-1)*(n-2)…*1。0的階乘為1。我們能想到一般的做法，就是用一個for循環，從第一個數乘到最後一個：

#big-o(n)
def f2(n):
if n == 0:
return 1
sum = 1
for i in range(1,n+1):
sum *= i
return sum

返回結果：

f2(3)
6

現在我們這樣考慮，如果我們n的階乘n!，要求(n+1)!，只要乘上n+1就可以了。也就是說：f(n+1)與f(n)始終存在著某種聯系。這和我們高中學習的數學歸納法非常相似。
把關系一步一步列出來：

f(n) = n * f(n-1)
f(n-1) = (n-1) * f(n)
.............
f(1) = 1 * f(0)
f(0) = 1 (Base)

這個時候需要停止，如果不停止就會進入死循環。所以，我們應當有一個base，這個base決定了程序在哪裡停止。這個問題裡，我們就要寫一個遇到f(0)時返回。這就是遞歸的意思了：一寫base二寫遞歸， 程序如下

#big-o(n)
def f(n):
if n == 0:
return 1
return n * f(n-1) #big-o(1) all n 

那遞歸和for循環相比有什麼異同點，對於for循環，我們記一次計算為o(1)，for就是把所有數遍歷一遍，做乘法運算，時間復雜度為big-o(n)；對於遞歸，每次return n*f(n-1) 這是一次乘法計算，遞歸n次，時間復雜度也為big-o(n)。

f(3000)
RecursionError: maximum recursion depth exceeded in comparison

如果我們用遞歸的方式計算3000的階乘，會出現這樣的問題，顯示超出遞歸深度的錯誤。
這是因為，每次遞歸調用的時候都會在棧裡面創建一個新的地址空間，而最大遞歸深度一般是1000左右。
這樣一看，好像並沒有什麼優勢，但在很多地方，遞歸有著他獨到的地方，我們一一來看。

斐波拉契數列

斐波拉契數列：1 1 2 3 5 8 13 21…每個數都是前倆個數的和。
我們能立刻找到遞歸關系: f(n) = f(n-1) + f(n-2)
但前提是n>= 3, f(3) = f(2) + f(1)，再往前走就出現錯誤了。
我們在這就要寫base了：如果n = 1或n = 2，就返回1，其余n就直接遞歸，程序就出來了：
①

def fibonacci1(n):
assert(n>=0)
if(n <= 2):
return 1
return fibonacci1(n-1) + fibonacci1(n-2)

運行結果:

fibonacci1(6)
8

我們來運行一下第40個數：

time fibonacci1(40)
Wall time: 21.8 s

一共花掉了21.8s，這肯定是不能夠被允許的。我們考慮這種遞歸方式的復雜度：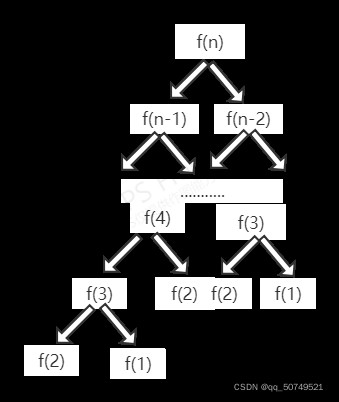

每次遞歸都用到了前兩次的遞歸結果，就像一棵樹一樣每根枝向下伸出兩根新枝，直到最後一根枝f(1)，最下面一行的f(1)出現了2^ n次。 這樣來看，時間復雜度為2^n。

如果我們用for循環來做，把每倆個看成一組，1 1 2 3 5 8 13 21…
（1,1）（1,2）（2,3）（3,5）（5,8）（8,13）（13,21）…
我們記每一組的倆個數分別為a，b。後一組的b是前一組的a+b，a是前一組的b。程序輸入我們想要的第n個數，就要做n-1次循環，程序如下：
②

def fibonacci2(n):
a = 1
b = 1
for i in range(n-1):
a, b = b, a + b
return a

簡化一下程序，按照這個規律往前推一位：(0,1) (1,1) (1,2) (2,3)…
求第n位就是進行n次循環

def fibonacci3(n):
a = 0
b = 1
for i in range(n):
a, b = b, a + b
return a

③
仍然選擇用遞歸來做，在解答①當中一次遞歸調用了前兩次結果。所以可以嘗試每次遞歸只調用一次結果，這裡用到②的思想，我們去返回一個組。
思路：把 （1,1）（1,2）（2,3）（3,5）（5,8）（8,13）這樣每一個組看作遞歸的結果，每次調用一個組。

def fibonacci4(n):
if n == 1:
return (1,1)
a, b = fibonacci4(n-1)
return (b, a + b)

返回結果

fibonacci4(4)
(3, 5)
fibonacci5(5)
(5, 8)

這樣我們對結果取出第一個數就可以了。

打印尺子

1

1 2 1

1 2 1 3 1 2 1

1 2 1 3 1 4 1 3 1 2 1

我們觀察f(n)和f(n+1)的關系。可以發現 f(n+1) 是這樣擺置的: f(n) n f(n)。
思路就有了：一先寫base，當n值降到1時，就return 1 。二寫遞歸

def ruler_bad(n):
if n == 1:
return '1'
return ruler_bad(n-1) + ' ' + str(n) + ' ' + ruler_bad(n-1)

ruler_bad(3)
'1 2 1 3 1 2 1'

結果正確，但機智的人就反映過來了，這裡每次遞歸調用了兩次ruler_bad(n-1)呀，和上一題fibonacci1出現了同樣的問題。再仔細看一眼，還是有點不一樣，這裡兩次調用的都是同一個東西! 那我們就可以做一個小correct：

def ruler_bad(n):
if n == 1:
return '1'
t = ruler_bad(n-1)
return t + ' ' + str(n) + ' ' + t

把前一次調用賦值給t，相當於只調用了一次，時間復雜度降為o(n), 完美！

下面我們開始畫尺子：

def draw_line2(n, mark=''):
if mark:
print('-'* n + mark)
else:
print('-' * n)
def draw_interval2(n):
if (n == 0):
return
draw_interval(n-1)
draw_line(n)
draw_interval(n-1)
def draw_rule2(n,length):
for i in range(length):
draw_line(n,str(i))
draw_interval(n)
draw_line(n,str(length))

結果：

draw_rule2(3, 2)
---0
-
--
-
---
-
--
-
---1
-
--
-
---
-
--
-
---2

數字表達式

給定a<=b ，a只能做乘2或加1的操作，找到最小操作順序使得a=b
23 = ((5 * 2+1) * 2+1)
解決這個問題需要逆向思維，不是考慮a怎麼變到b，而是考慮b怎麼降到a更容易。
我們首先想到的就是，把b和2倍的a相比，如果>2a就除2，如果小於2a，那麼b只要一直減去1就行了。
值得注意的是，因為可能要除2，所以在與2a相比較之前，把b變成一個偶數。
如果b本來就是偶數，不變。如果b本來是奇數，對b-1，最後結果再加一就可以了。

寫程序之前我們舉個例子：a = 5,b = 23
23為奇數-> 23 - 1 = 22
22 > 2*5 -> 22 / 2 = 11
11為奇數-> 11 - 1 = 10
10/2 = 5 =a 返回a
第一步，寫base，這道題的base就是b降到和a一樣大的時候，返回a。第二步按先奇偶再比較的順序寫遞歸：

def intseq(a, b):
if a == b:
return str(a)
if b % 2 == 1:
return '(' + intseq(a, b-1) + '+1)'
if b >= 2 * a:
return intseq(a, b//2) + '*2'
if b < 2 * a:
return '(' + intseq(a, b-1) + '+1)'

結果：

a = 11
b = 23
print(str(b) + '=' + intseq(a,b))

23=(11*2+1)

套圈——漢諾塔問題

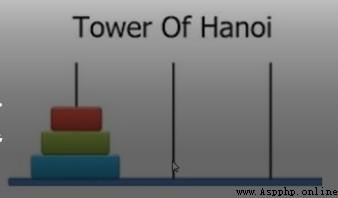
一共三個桿子，左中右分別記為start，by，end。一開始第一個桿子上套了n個圈，只能從小到大排。現在要把這些圈從小到大放到最右邊的桿子上，每次只能移動一個桿子，求最小路徑。

我們以3個圈為例，紅->end, 綠->by, 紅->by，藍->end, 紅->start, 綠->end, 紅->end
一共花費了7次 。可以感受到，我們是把紅綠這倆個擺到中間，藍色擺到末位，最後把紅綠擺過去，這就是遞歸的意味了。

假設現在有n+1個圈子，那我們就可以先把上面的n個圈子，擺到中間，第n+1個擺到末位，最後再把前n個擺過來，就可以了。

同樣的道理，先寫base再寫遞歸。這裡的base，就是n降為1的時候
我們定義函數hanoi(n, start, by, end):

def hanoi(n, start, end, by):
if n == 1:
print("start from " + start + " to " + end)
else:
hanoi(n-1, start, by, end)
hanoi(1, start, end, by)
hanoi(n-1, by, end, start)

結果

hanoi(3, "start", "end", "by")
start from start to end
start from start to by
start from end to by
start from start to end
start from by to start
start from by to end
start from start to end

打印子集Subset

舉個例子：求出{1,2,3}的所有子集.
一一列出：[] [1] [2] [3] [1,2] [1,3] [2,3] [1,2,3]

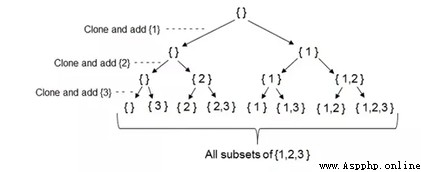
思路1：首先定義一個空數組，復制並我們append原集的第一個數，得到[]和[1]。第二步，復制上一步的[]和[1]並append原集的第二個數，以此類推。

def Subset(nums):
result = [[]]
for num in nums:
for element in result[:]:
x = element[:]
x.append(num)
result.append(x)
return result

這裡要注意程序編寫時，第一處result要copy一份result[:]，否則會陷入死循環，這是因為我們在第二個for循環裡就是對result做增添元素操作，增添之後又會遍歷到這個元素。比如第一步加入[1]，element只等於[]，result增添元素之後變成了[[],[1]],此時應當循環結束了。但是，程序返回來又去遍歷result，element就變成了新加進去的[1]，如此循環沒有盡頭。
第二步，result裡的元素element也要copy，如果沒有copy，就會出現這樣的結果:

[[1, 2, 2, 3, 3, 3, 3],
[1, 2, 2, 3, 3, 3, 3],
[1, 2, 2, 3, 3, 3, 3],
[1, 2, 2, 3, 3, 3, 3],
[1, 2, 2, 3, 3, 3, 3],
[1, 2, 2, 3, 3, 3, 3],
[1, 2, 2, 3, 3, 3, 3],
[1, 2, 2, 3, 3, 3, 3]]

每個返回的元素都是一樣的，這是因為上一次append後的element會繼承到第二次循環裡。比如result裡現在是[]和[1]，element第一次取[]，加入2，element變成[2]，result裡也加入[2]，第二次遍歷element=[1]時，再加入2,本應該是[1,2]，這個時候卻變成了[1,2,2]，上一次循環留下來的2沒有清除掉，就出現了這樣的錯誤，把握細節很重要。

思路2：

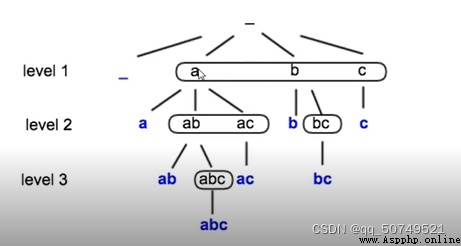
從第一個數a開始向下走，保留或繼續選第二個數，首先得到a，ab，ac。對於ab，往下走得到ab或abc，ac往下走還是ac，abc往下走也還是abc，不能再往下走後原路返回，搜尋這個路徑下的其他可能情況，一直到第一個數b開始。

def subsets_recursive(nums):
lst = []
result = []
subsets_recursive_helper(result, lst, nums, 0);
return result
def subsets_recursive_helper(result, lst, nums, pos):
result.append(lst[:])
for i in range(pos, len(nums)):
lst.append(nums[i])
subsets_recursive_helper(result, lst, nums, i+1)
lst.pop()

nums = ['a','b','c']
subsets_recursive(nums)

[[], ['a'], ['a', 'b'], ['a', 'b', 'c'], ['a', 'c'], ['b'], ['b', 'c'], ['c']]