Let's first implement factorial initially,也就是 n! = n*(n-1)*(n-2)…*1.0的階乘為1.We can think of common practices,就是用一個for循環,Multiply from the first number to the last:
#big-o(n)
def f2(n):
if n == 0:
return 1
sum = 1
for i in range(1,n+1):
sum *= i
return sum
返回結果:
f2(3)
6
Now we think about it this way,如果我們n的階乘n!,要求(n+1)!,Just multiplyn+1就可以了.也就是說:f(n+1)與f(n)There is always some connection.This is very similar to the mathematical induction we learned in high school.
List the relationships step by step:
f(n) = n * f(n-1)
f(n-1) = (n-1) * f(n)
.............
f(1) = 1 * f(0)
f(0) = 1 (Base)
這個時候需要停止,If it doesn't stop, it will enter an infinite loop.所以,We should have onebase,這個baseDetermines where the program stops.這個問題裡,We're going to write an encounterf(0)時返回.This is what recursion means:一寫baseSecond write recursion, 程序如下
#big-o(n)
def f(n):
if n == 0:
return 1
return n * f(n-1) #big-o(1) all n
That recursive sumforWhat are the similarities and differences compared to the cycle,對於for循環,We record a calculation as o(1),forJust loop over all the numbers,做乘法運算,時間復雜度為big-o(n);對於遞歸,每次return n*f(n-1) This is a multiplication calculation,遞歸n次,時間復雜度也為big-o(n).
f(3000)
RecursionError: maximum recursion depth exceeded in comparison
If we calculate it recursively3000的階乘,會出現這樣的問題,Shows the error that the recursion depth is exceeded.
這是因為,Each recursive call creates a new address space on the stack,And the maximum recursion depth is generally 1000左右.
這樣一看,好像並沒有什麼優勢,但在很多地方,Recursion has its own unique place,我們一一來看.
斐波拉契數列:1 1 2 3 5 8 13 21…Each number is the sum of the previous two numbers.
We can immediately find the recursion relation: f(n) = f(n-1) + f(n-2)
但前提是n>= 3, f(3) = f(2) + f(1),Going any further, an error occurs.
We're going to write herebase了:如果n = 1或n = 2,就返回1,其余n就直接遞歸,程序就出來了:
①
def fibonacci1(n):
assert(n>=0)
if(n <= 2):
return 1
return fibonacci1(n-1) + fibonacci1(n-2)
運行結果:
fibonacci1(6)
8
Let's run the first40個數:
time fibonacci1(40)
Wall time: 21.8 s
A total of spent21.8s,This is definitely not allowed.We consider the complexity of this recursive approach: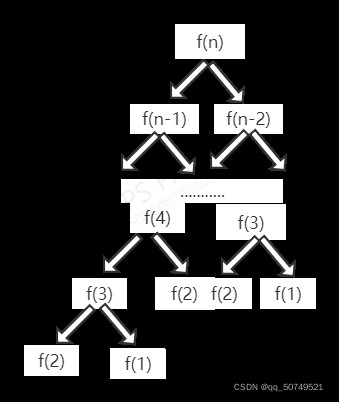
Each recursion uses the previous two recursion results,Like a tree, each branch extends downward with two new branches,until the last branchf(1),最下面一行的f(1)出現了2^ n次. 這樣來看,時間復雜度為2^n.
如果我們用for循環來做,Think of each as a group,1 1 2 3 5 8 13 21…
(1,1)(1,2)(2,3)(3,5)(5,8)(8,13)(13,21)…
We record the two numbers of each group as a,b.the latter groupbof the previous groupa+b,aof the previous groupb.The program enters the number we wantn個數,就要做n-1次循環,程序如下:
②
def fibonacci2(n):
a = 1
b = 1
for i in range(n-1):
a, b = b, a + b
return a
Simplify the procedure,Move forward one place according to this rule:(0,1) (1,1) (1,2) (2,3)…
求第nA bit is going onn次循環
def fibonacci3(n):
a = 0
b = 1
for i in range(n):
a, b = b, a + b
return a
③
Still choose to do it with recursion,在解答①One of the recursive calls to the first two results.So one can try to call the result only once per recursion,這裡用到②的思想,Let's go back to a group.
思路:把 (1,1)(1,2)(2,3)(3,5)(5,8)(8,13)Thus each group is seen as the result of recursion,One group is called at a time.
def fibonacci4(n):
if n == 1:
return (1,1)
a, b = fibonacci4(n-1)
return (b, a + b)
返回結果
fibonacci4(4)
(3, 5)
fibonacci5(5)
(5, 8)
In this way, we can take the first number of the result.
1
1 2 1
1 2 1 3 1 2 1
1 2 1 3 1 4 1 3 1 2 1
我們觀察f(n)和f(n+1)的關系.可以發現 f(n+1) It's laid out like this: f(n) n f(n).
思路就有了:write firstbase,當n值降到1時,就return 1 .Second write recursion
def ruler_bad(n):
if n == 1:
return '1'
return ruler_bad(n-1) + ' ' + str(n) + ' ' + ruler_bad(n-1)
ruler_bad(3)
'1 2 1 3 1 2 1'
結果正確,But smart people reflected on it,Here each recursive call is made twiceruler_bad(n-1)呀,和上一題fibonacci1出現了同樣的問題.再仔細看一眼,還是有點不一樣,Both calls here are the same thing! Then we can make a small onecorrect:
def ruler_bad(n):
if n == 1:
return '1'
t = ruler_bad(n-1)
return t + ' ' + str(n) + ' ' + t
Assign the previous call to t,Equivalent to only called once,時間復雜度降為o(n), 完美!
Now let's start drawing the ruler:
def draw_line2(n, mark=''):
if mark:
print('-'* n + mark)
else:
print('-' * n)
def draw_interval2(n):
if (n == 0):
return
draw_interval(n-1)
draw_line(n)
draw_interval(n-1)
def draw_rule2(n,length):
for i in range(length):
draw_line(n,str(i))
draw_interval(n)
draw_line(n,str(length))
結果:
draw_rule2(3, 2)
---0
-
--
-
---
-
--
-
---1
-
--
-
---
-
--
-
---2
給定a<=b ,aOnly multiply2或加1的操作,Find the minimum order of operations such that a=b
23 = ((5 * 2+1) * 2+1)
Solving this problem requires reverse thinking,不是考慮a怎麼變到b,而是考慮bHow to come downa更容易.
我們首先想到的就是,把b和2倍的a相比,如果>2a就除2,如果小於2a,那麼b只要一直減去1就行了.
值得注意的是,Because it may be removed2,所以在與2a相比較之前,把bbecomes an even number.
如果bIt was an even number,不變.如果bOriginally an odd number,對b-1,The final result can be added one more.
Let's take an example before writing a program:a = 5,b = 23
23為奇數-> 23 - 1 = 22
22 > 2*5 -> 22 / 2 = 11
11為奇數-> 11 - 1 = 10
10/2 = 5 =a 返回a
第一步,寫base,這道題的base就是b降到和a一樣大的時候,返回a.The second step writes the recursion in the order of parity first and then comparison:
def intseq(a, b):
if a == b:
return str(a)
if b % 2 == 1:
return '(' + intseq(a, b-1) + '+1)'
if b >= 2 * a:
return intseq(a, b//2) + '*2'
if b < 2 * a:
return '(' + intseq(a, b-1) + '+1)'
結果:
a = 11
b = 23
print(str(b) + '=' + intseq(a,b))
23=(11*2+1)
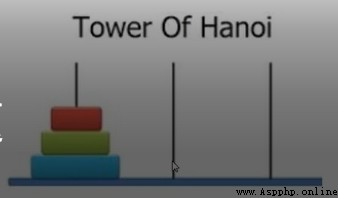
Three poles in total,Left, middle and right respectivelystart,by,end.At first the first pole was put onn個圈,Only from small to large.Now place the circles from smallest to largest on the rightmost pole,Only move one pole at a time,求最小路徑.
我們以3circle for example,紅->end, 綠->by, 紅->by,藍->end, 紅->start, 綠->end, 紅->end
一共花費了7次 .可以感受到,We put red and green in the middle,Blue to the end,Finally put the red and green in the past,This is what recursion means.
假設現在有n+1個圈子,Then we can put the above firstn個圈子,Put it in the middle,第n+1one to the end,Finally put the frontnA swing over,就可以了.
同樣的道理,先寫baseWrite recursion again.這裡的base,就是n降為1的時候
我們定義函數hanoi(n, start, by, end):
def hanoi(n, start, end, by):
if n == 1:
print("start from " + start + " to " + end)
else:
hanoi(n-1, start, by, end)
hanoi(1, start, end, by)
hanoi(n-1, by, end, start)
結果
hanoi(3, "start", "end", "by")
start from start to end
start from start to by
start from end to by
start from start to end
start from by to start
start from by to end
start from start to end
舉個例子:求出{1,2,3}的所有子集.
一一列出:[] [1] [2] [3] [1,2] [1,3] [2,3] [1,2,3]
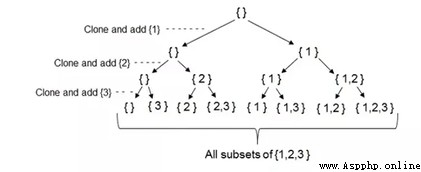
思路1:First define an empty array,Copy and weappendThe first number of the original set,得到[]和[1].第二步,復制上一步的[]和[1]並appendThe second number of the original set,以此類推.
def Subset(nums):
result = [[]]
for num in nums:
for element in result[:]:
x = element[:]
x.append(num)
result.append(x)
return result
Pay attention here when writing the program,第一處result要copy一份result[:],否則會陷入死循環,This is because we are in the secondforThe loop is rightresultDo add element operation,After adding, it will traverse to this element again.For example, the first step to join[1],element只等於[],resultAfter adding elements, it becomes[[],[1]],At this point the loop should be over.但是,The program goes back and forth and traversesresult,elementhas become a new addition[1],There is no end to this cycle.
第二步,result裡的元素element也要copy,如果沒有copy,就會出現這樣的結果:
[[1, 2, 2, 3, 3, 3, 3],
[1, 2, 2, 3, 3, 3, 3],
[1, 2, 2, 3, 3, 3, 3],
[1, 2, 2, 3, 3, 3, 3],
[1, 2, 2, 3, 3, 3, 3],
[1, 2, 2, 3, 3, 3, 3],
[1, 2, 2, 3, 3, 3, 3],
[1, 2, 2, 3, 3, 3, 3]]
Each returned element is the same,It's because of the last timeappend後的elementwill be inherited into the second loop.比如resultis now[]和[1],element第一次取[],加入2,element變成[2],resultalso joined[2],第二次遍歷element=[1]時,再加入2,本應該是[1,2],This time it has become[1,2,2],Left over from the last cycle2沒有清除掉,就出現了這樣的錯誤,It is important to grasp the details.
思路2:
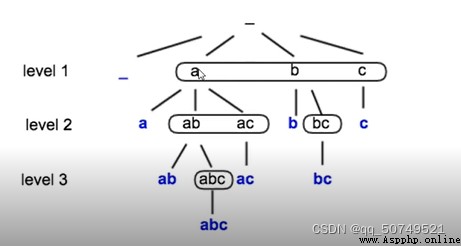
從第一個數aStart going down,Keep or continue to choose the second number,首先得到a,ab,ac.對於ab,Go down to get itab或abc,acStill going downac,abcStill going downabc,You can't go down any further and go back the same way,Search for other possibilities under this path,all the way to the first numberb開始.
def subsets_recursive(nums):
lst = []
result = []
subsets_recursive_helper(result, lst, nums, 0);
return result
def subsets_recursive_helper(result, lst, nums, pos):
result.append(lst[:])
for i in range(pos, len(nums)):
lst.append(nums[i])
subsets_recursive_helper(result, lst, nums, i+1)
lst.pop()
nums = ['a','b','c']
subsets_recursive(nums)
[[], ['a'], ['a', 'b'], ['a', 'b', 'c'], ['a', 'c'], ['b'], ['b', 'c'], ['c']]