01背包問題 ( 01 Knapsack problem)

有10件貨物要從甲地運送到乙地,每件貨物的重量(單位:噸)和利潤(單位:元)如下表所示:

由於只有一輛最大載重為30t的貨車能用來運送貨物,所以只能選擇部分貨物配送,要求確定運送哪些貨物,使得運送這些貨物的總利潤最大。

1.1 原問題和子問題

原問題: 在滿足重量約束的條件下,將這m件物品選擇性的放入容量為W的背包中所能獲得的最大利潤.

子問題: 在滿足重量約束的條件下,將前i (i <=m) 件物品選擇性的放入容量為 (j<=W) 的背包中所能獲得的最大利潤.

其實這個問題我們可以采用自上而下的迭代，創建一個長為容量，寬為數量的二維矩陣，從第一行開始，第一行代表第一個物品，從左到右重量夠的取最優解，然後開始第二行，即第二個物品，此時最優解涉及到第一個，可參考上一行的最優解，同第二個物品比較，得出兩個物品的最優解…以此類推

1.2 尋找物品編號

我們現在來看一個例子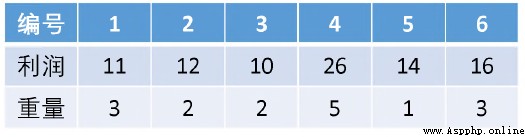

由於我們創建的那個表格是 物品和容量，所以先選出最後一列中取出最大的，然後回到上面的表，減去對應的物品編號，得出上一個物品，得出剩余的背包空間，以此類推，很像禮物問題的求出禮物編號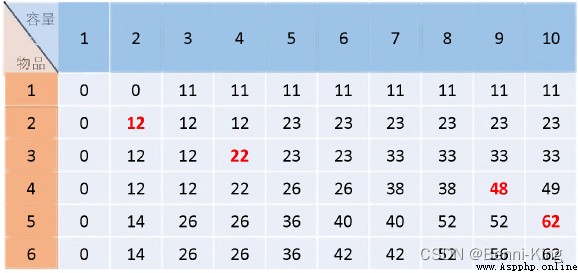

python 解法

import numpy as np
class solution():
def __init__(self):
self.profile= [11,12,10,26,14,16]
self.weight = [3, 2 ,2, 5, 1, 3]
self.W=10
def total(self):
ind=0
num = len(self.profile)
DP = np.zeros((num,self.W))
#第一行
if self.weight[0] < self.W :
DP[0,(self.weight[0]-1):(self.W)]=self.profile[0]
#第一列
for i in range(1,num):
for each in self.weight[0:i]:
if each ==1:
IND=self.weight.index(1)
DP[i-1:num,0]=self.profile[IND]
ind=1
break
if ind==0:
DP[i,0]=0
for i in range(1,num):
for j in range(1,self.W):
if self.weight[i] > j+1:
DP[i,j]= DP[i-1,j]
elif self.weight[i] == j+1:
DP[i,j]=max(DP[i-1,j],self.profile[i])
else:
DP[i,j]=max(DP[i-1,j],self.profile[i]+DP[i-1,j-self.weight[i]])
return DP
def Object(self,DP):
if len(DP)>0:
Object_num=[]
num = len(self.profile)
ww=self.W
tmp=list(DP[0:num,self.W-1])
while 1:
ind=tmp.index(max(tmp))
ww=ww-self.weight[ind]
Object_num.append(ind+1)
if ((ind>1) ==True) and ((ww>0) ==True):
tmp=list(DP[0:ind,ww-1])
else:
break
result=Object_num.sort()
else:
return -1
return result
backpack=solution()
DP=backpack.total()
print(DP)
Object_num=backpack.Object(DP)
print(Object_num)

matlab 解法

p = [540,200,180,350,60,150,280,450,320,120]; %利潤
w = [6 ,3, 4 ,5, 1, 2, 3, 5, 4, 2]; %重量
W = 30; %容量
f = knapsack01problem1(p,w,W)
function [f, IND] = knapsack01problem2(p,w,W)
% 輸入： p：物品的利潤 w：物品的重量 W：背包的容量
% 為了編程方便，假設W是大於等於2的正整數；w中每個元素都是大於等於1的正整數
m = length(p); % 物品個數
FF = zeros(m,W); % 初始化DP數組
% FF(i,j)：前i件物品選擇性的放入容量為j的背包中所能獲得的最大利潤
if w(1) <= W % 初始化第一行
FF(1,w(1):end) = p(1);
end
for i = 2:m % 初始化第一列
FF(i,1) = max([p(w(1:i) == 1),0]);
end
% i,j>1的情況
for i = 2:m
for j = 2:W
if w(i) > j % 第i件物品的重量w(i)比背包的容量j還要大
FF(i,j) = FF(i-1,j) ;
elseif w(i) == j % 第i件物品的重量w(i)等於背包的容量j
FF(i,j) = max(FF(i-1,j), p(i)); % 不放進去和放進去取較大的值
else % 第i件物品的重量w(i)小於背包的容量j
FF(i,j) = max(FF(i-1,j), p(i)+FF(i-1,j-w(i))); % 不放進去和放進去取較大的值
end
end
end
f = FF(m,W);
IND = []; % 選擇的物品編號IND初始化為空
if f > 0 % 只要有利潤，就可以利用FF來計算選擇的物品編號IND
ww = W; % 初始化背包的剩余容量為整個背包的容量W
tmp = FF(:,ww); % 取出最後一列
while 1 % 不斷循環下去，後面通過條件判斷來退出循環
ind = find(tmp == max(tmp),1) ; % 找到裝入背包的那個物品
ww = ww - w(ind); % 更新背包的剩余容量
IND = [IND,ind]; % 更新IND裡面的元素
if ind > 1 && ww>0 % 只要不是第一個物品或者背包容量為空
tmp = FF(1:ind-1,ww); % 重新取出剩余容量的那一列（只保留前面的物品）
else
break % 跳出循環
end
end
IND = sort(IND); % 排序下，輸出好看點
end
end