由於網上搜到關於漢明碼矩陣計算的資料比較少,基本上都是(7,4)居多,有些還是用class定義的,感覺很不友好。現在就來補充一點資料吧。
關於漢明碼手算基本過程,大家可以參考漢明碼手算,對漢明碼編碼有一個大概了解
一個數如果是2的N次冪,那它的二進制必定只有一個1其余為0,要想判斷一個數是否是2的N次冪,只需把這個數減1,然後按位與,判斷結果是否為0。
用8來舉例子
代碼實現如下
if num & num-1 ==0: #Ture則為2的N次冪
本代碼會涉及到很多list和漢明碼位數的使用,list的index是從0開始,而漢明碼第一位我們認為是1,所以兩者相差了1,打代碼要小心。
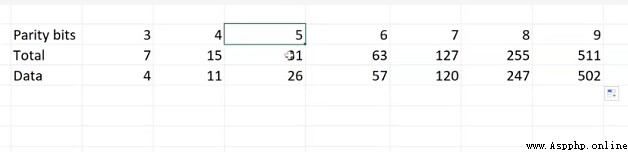
根據excel,我們可以看出他們之間的關系的規律,並得出如下式子
校驗位 parity bit 這裡簡寫成P

上面1.3講過了,三個位數之間是有關系的,我們可以用代碼來找,這裡為了方便我的data用了4位方便學習,後續可自行改成任意長度
print("welcome to use the code made by Benni-Kang")
data='1101'
len_data=len(data)
Par_bits=0
while(len_data+1>2**Par_bits - Par_bits):
Par_bits+=1
print('Number of Parity Bits=',Par_bits)
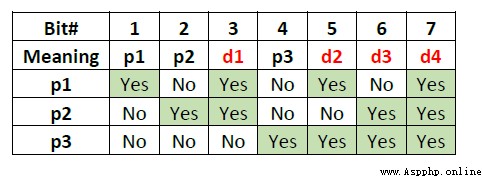
這是把每一位的2進制寫在下面表格,而且是倒著寫 如1的二進制001,在這裡就是從下往上寫。把這個表格拿出來變成矩陣就是H
import numpy as np
import pandas as pd
column = []
j=-1
for i in range(1,total_bits+1): #1 /7
num =bin(i)
while num[j] != "b":
column+=num[j]
j-=1
j=-1
column = list(map(int,column))
if i==1:
col= pd.DataFrame(column,columns=['1'])
else:
column =pd.DataFrame(column,columns=[str(i)])
H_dataframe=pd.concat([col,column],axis=1)
col=H_dataframe
column=[]
H_dataframe.fillna(0,inplace=True)# 空缺補0
H_dataframe.index=H_dataframe.index+1 #從1開始索引
H_matrix = np.array(H_dataframe)
這裡的datafame可以看成是一個表格,像excel,並不是矩陣,不過可以轉換成矩陣來計算
unit_matrix=np.eye(len_data)#創建單位矩陣
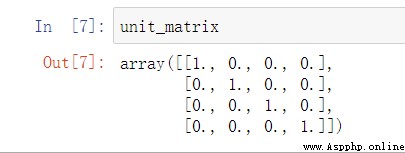
把H的(1,2,4)列去掉,然後在新的矩陣的1,2,4行按順序插入單位矩陣,就變成了G矩陣
for i in range(1,total_bits+1):
if i & i-1 == 0:
print(i)
H_dataframe.drop(str(i), axis=1,inplace=True)
g_matrix=H_dataframe
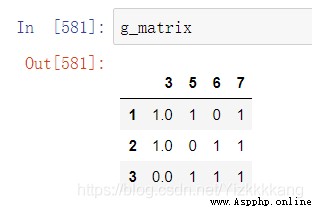
g_matrix是去除掉的,現在下面來插入
j=0
for i in range(1,total_bits+1):
if i & i-1 == 0:
# print("1111",i)
G_matrix=np.insert(unit_matrix, i-1, g_matrix.iloc[j], axis=0)
unit_matrix=G_matrix
# print(j)
# print(g_matrix.iloc[j])
j+=1
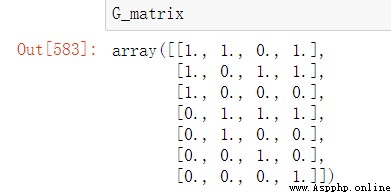
這個沒有什麼好講的…
data_list=[]
for char in data:
data_list.append(char)
data_list = list(map(int,data_list))
關於這個矩陣乘的線代計算,可以參考我的numpy學習筆記中2.3.2有提及具體的內容
首先當然是轉換成矩陣,一維矩陣轉置在這裡是沒有意義的,所以列向量行向量都一樣,然後我們把G和data兩個矩陣相乘,然後在轉換成list類型
data_matrix =np.array(data_list) #轉換為array
r_matrix=np.dot(G_matrix,data_matrix)
r_list=r_matrix.tolist()
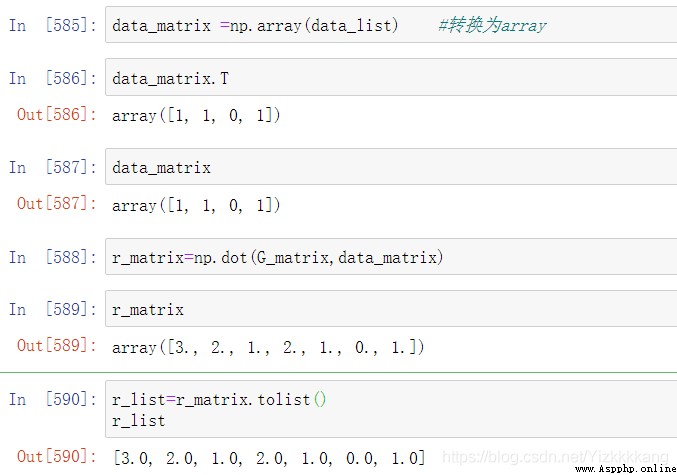
這裡的意思就是計算出一個數的二進制的最小位
encode=[]
for num in r_list:
mod2 = num % 2
encode.append(int(mod2))
print("The encoded message is ",encode)
產生隨機數,並翻轉
import random
def flip_bit(message, location):
# This will flip the bit at position e-1 (0->1 and 1->0)
message[location] = 1 - message[location]
print("welcome to use the code made by Benni-Kang")
return message
def flip_random_bit(message):
e = random.randint(1, len(message))
print("Flipping bit (=introducing error) at location: " + str(e))
# This will flip the bit at position e-1 (0->1 and 1->0)
message = flip_bit(message, e-1)
return message
糾錯就是,拿H矩陣和encoded的矩陣相乘之後如果沒錯,結果為0,如果有錯,結果為錯誤的位數,而且這裡的二進制要倒著寫,最高位是H0,最低位反而是Hn(n為校驗位個數)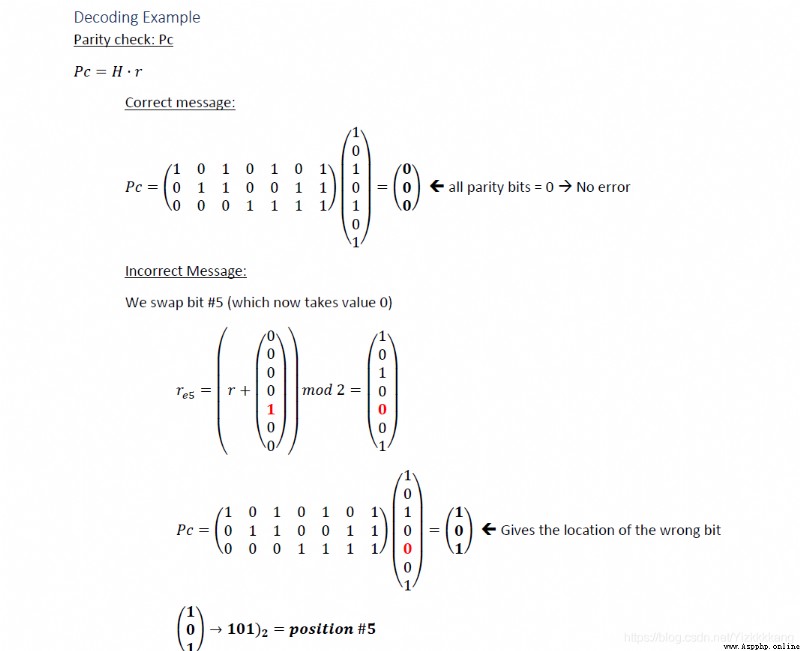
reveiver_message_matrix =np.array(reveiver_message)
Pc=np.dot(H_matrix,reveiver_message_matrix)
Pc_list=Pc.tolist()
print(Pc_list)
receive_bits=[]
for num in Pc_list:
mod2 = num % 2
receive_bits.append(int(mod2))
bi_to_di=''
for i in range(1,len(receive_bits)+1):
bi_to_di+= str(receive_bits[-i])
error_position= int(bi_to_di,2)
if error_position!=0:
message=flip_bit(reveiver_message, error_position-1)
print(message)
這裡用到的方法都是array類型,也有用list做出來同樣效果的,比如直接用去掉124位的H和data直接乘,就變成校驗位,然後再把校驗位插入數據的list就變成了encode message。我這裡舉些代碼例子,只是為了演示想法,不是本體具體解法。
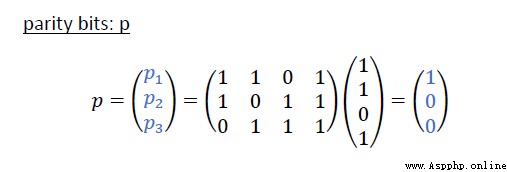
由於刪除1,2,4位會導致list的刪改,所以我們要用到reserve()函數,從高位開始刪除,這樣就不會造成錯誤,可以自行刪除看會發生什麼
刪除list中的1,2,4位代碼舉例如下:
插入的代碼如下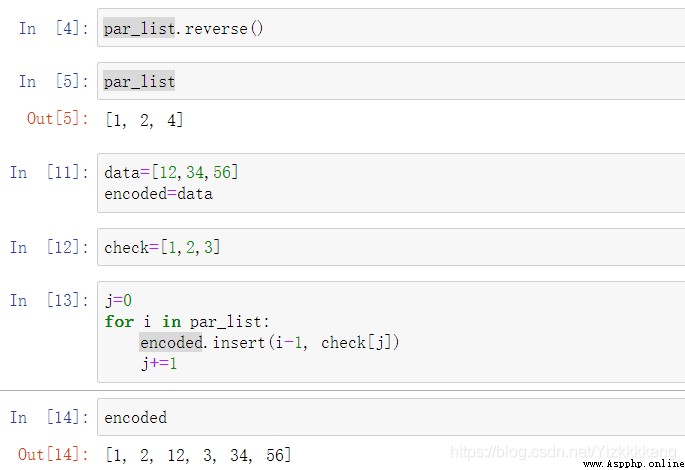
 Python based course management intelligent course scheduling system course paper + design process drawing + source code and database file
Python based course management intelligent course scheduling system course paper + design process drawing + source code and database file
Catalog Chapter one Introduct
 Based on python, the admission scores of 2822 colleges and universities in all provinces in the past three years were obtained
Based on python, the admission scores of 2822 colleges and universities in all provinces in the past three years were obtained
Recently, the national college