您现在的位置：程式師世界 >> 編程語言 > >> 更多編程語言 >> Python

淺談K-means算法和實現(基於Python)

編輯：Python

Kmeans可視化
https://www.naftaliharris.com/blog/visualizing-k-means-clustering/

K-means原理

K-means 有一個著名的解釋：牧師—村民模型：

有四個牧師去郊區布道，一開始牧師們隨意選了幾個布道點，並且把這幾個布道點的情況公告給了郊區所有的村民，於是每個村民到離自己家最近的布道點去聽課。
聽課之後，大家覺得距離太遠了，於是每個牧師統計了一下自己的課上所有的村民的地址，搬到了所有地址的中心地帶，並且在海報上更新了自己的布道點的位置。
牧師每一次移動不可能離所有人都更近，有的人發現A牧師移動以後自己還不如去B牧師處聽課更近，於是每個村民就去了離自己最近的布道點……
就這樣，牧師每個禮拜更新自己的位置，村民根據自己的情況選擇布道點，最終穩定了下來

Kmeans，一種無監督聚類算法，也是最為經典的基於劃分的聚類方法，思想是: 對於給定的樣本集，按照樣本之間的距離大小，將樣本集劃分為K個類。讓類內的點盡量緊密的連在一起，而讓類間的距離盡量的大
步驟:

先確定數據集類的個數k
數據預處理: 剔除離群點(剔除掉那些可能由人為因素造成的，並非真實數據的樣本點)、數據歸一化(消除量綱的影響，轉換方法為: (X - min) / (max - min) )、數據標准化(將采集到的數據分布轉換成標准正態分布，轉換公式: X減去均值，再除以標准差)
在數據集中隨機選取k個數據，作為初始質心
計算數據集中每個樣本到每個質心的歐式距離，把樣本劃分到距離最小的質心所屬的類別
根據聚類結果，重新計算質心，使用的是求均值的方法進行更新: μ i = 1 m i ∑ x j ∈ C i x j μ_i = \frac{1}{m_i}\sum_{x_j∈C_i} {x_j} μi=mi1∑xj∈Cixj 其中，C_i是第i個類，x_j是C_i中的樣本點，μ_i是第i個類的類中心點，m_i是第i個類中的樣本點個數 (注意新的質心不一定是實際的樣本點)，當本次計算的質心與上一次質心完全一樣（或者收斂）時，停止迭代；否則更新質心，重復執行3、4兩步操作
考慮到臨近性度量是歐幾裡得距離，使用誤差的平方和(SSE指標)，作為度量聚類質量的好壞，後面再講

例子: https://www.bilibili.com/video/BV1py4y1r7DN?share_source=copy_web
有以下6個點，將A3和A4作為初始質心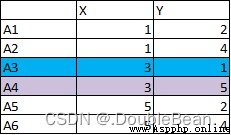

1.計算每個點到質心距離，將距離近的點歸為一類。從下圖可以看到A1與A3的距離是2.24，與A4的距離是3.61，所以A1被歸為A3這一類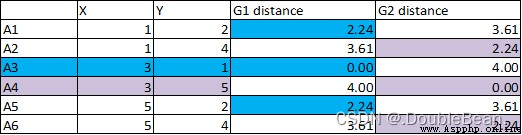

2.將藍色每個點，和紫色每個點的x,y值分別求平均。獲得新的質心

3.計算每個點到質心的新距離，將距離近的點歸為一類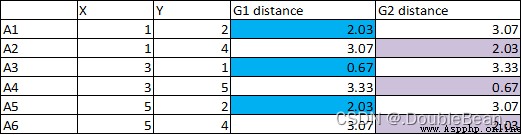

4.由於關聯點沒有變化，所以之後的計算結果不會改變，停止計算
5.藍色類: A1, A3, A5。紫色類：A2, A4, A6。

代碼實現

# 不調庫實現
class my_Kmeans:
def __init__(self, k):
self.k = k
# 距離度量函數: 計算任意點之間的距離
def calc_distance(self, vec1, vec2):
return np.sqrt(np.sum(np.power(vec1 - vec2, 2)))
def fit(self, data):
numSamples, dim = data.shape # numSamples指樣本總數，dim指特征維度
# 隨機並且不重復地選取k個數據作為初始聚類中心點
self.centers_idx = np.random.choice(numSamples, self.k, replace=False) # 得到的是質心點的索引
self.centers = data[self.centers_idx].astype(np.float32) # 初始化聚類中心
# ClusterAssment記錄每個樣本的信息: 第一列記錄樣本所屬聚類中心的索引，第2列記錄樣本與聚類中心的距離的平方(用於SSE指標)
ClusterAssment = np.zeros((numSamples, 2))
ClusterChanged = True
while ClusterChanged:
ClusterChanged = False
# 遍歷所有點求每個點與各個聚類中心點的距離
for i in range(numSamples):
mindist = self.calc_distance(data[i], self.centers[0])
label = 0
for j in range(1, self.k):
distance = self.calc_distance(data[i], self.centers[j])
# 把第i個數據分配到距離最近的聚類中心
if distance < mindist:
mindist = distance
label = j
# print("mindist = {}，label = {}".format(mindist, label))
# 判斷樣本所屬聚類中心是否發生了變化，若發生了變化則更新數據
if ClusterAssment[i, 0] != label:
ClusterChanged = True
ClusterAssment[i, :] = label, mindist ** 2
# print(ClusterAssment, '\n')
# 對每個類別的樣本重新求聚類中心，並更新聚類中心
for j in range(self.k):
# 找到所有屬於類中心j的樣本數據
pointsInCluster = data[ClusterAssment[:, 0] == j]
# print("{}: {}".format(j, pointsInCluster))
self.centers[j, :] = (np.mean(pointsInCluster, axis=0).tolist()) # 更新聚類中心的位置
def predict(self, data):
numSamples, dim = data.shape
ClusterAssment = np.zeros((numSamples, 2))
for i in range(numSamples):
mindist = self.calc_distance(data[i], self.centers[0])
label_pred = 0
for j in range(1, self.k):
distance = self.calc_distance(data[i], self.centers[j])
if distance < mindist:
mindist = distance
label_pred = j
ClusterAssment[i, :] = label_pred, mindist ** 2
return self.centers, ClusterAssment

生成一些數據集，來檢驗Kmeans聚類效果

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_blobs
data, true_labels = make_blobs(centers = 5, random_state = 20, cluster_std = 1) # data是坐標集合，ture_labels是正確標簽
plt.scatter(data[:, 0], data[:, 1])
plt.show()

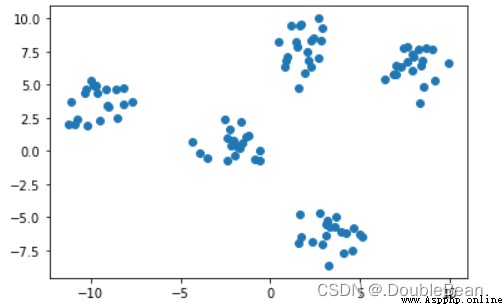
# 不調庫實現
model = my_Kmeans(k=5)
model.fit(data)
''' model.fit()函數返回值 centers: 聚類中心坐標 ClusterAssment: 每個樣本的信息: 第一列記錄樣本所屬聚類中心的索引，第2列記錄樣本與聚類中心的距離的平方(用於SSE指標) '''
centers, ClusterAssment = model.predict(data)
plt.figure(figsize=(6, 5))
plt.scatter(data[:, 0], data[:, 1], c = ClusterAssment[:, 0])
plt.scatter(centers[:, 0], centers[:, 1], marker = '*', color = 'r', s = 100) # 繪制類中心點
plt.show()

下圖便是代碼跑出來的結果，多運行幾次會發現不調庫實現的Kmeans聚類結果會各種各樣，即不調庫實現的Kmeans結果大部分情況下都是局部最優，並非全局最優

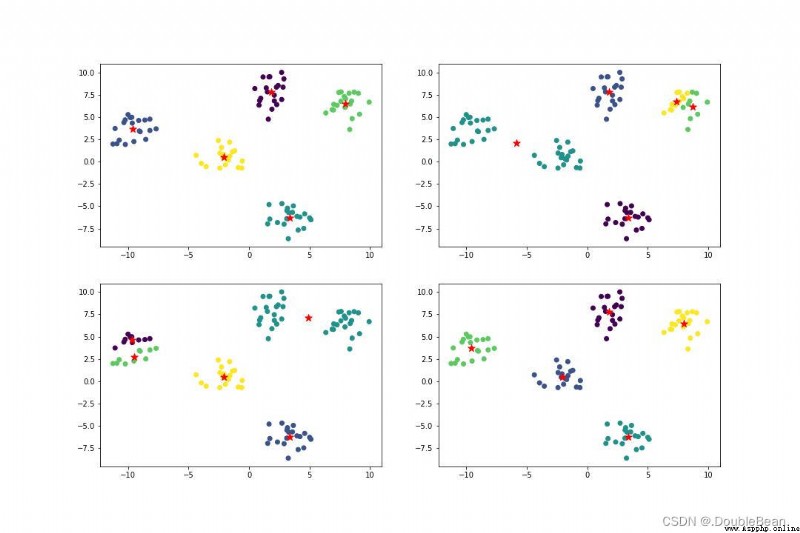
調庫實現的話，無論運行多少次，結果都很好

# 調庫實現
from sklearn.cluster import KMeans
model_1 = KMeans(n_clusters=5)
label_pred_1 = model_1.fit_predict(data)
plt.figure(figsize=(6, 5))
plt.scatter(data[:, 0], data[:, 1], c = label_pred_1)
plt.show()

缺點:

對初始的類中心敏感，步驟2隨機選取數據作為初始質心，可以想象，當質心之間距離很近的時候，將需要迭代很多次，會影響收斂速度，而且有可能最終只能得到局部最小值
步驟3中計算距離，我們應該想到，距離受到量綱的影響，在使用時，需要考慮一下歸一化；而且因為是應用於所有樣本，所以會對異常數據比較敏感，對孤立點數據非常敏感，少量的噪聲數據就能對平均值造成極大的影響，所以穩定性較差
Q: 前面數據預處理部分不是已經將離群點剔除了嗎？為什麼還會受離群點的影響？
A: 有些離群點是很容易判斷出來的，但有些離群點並不好判斷，比如說離群點處於數據分布的邊緣，我們並不知道它是真實數據還是離群點，所以還是有離群點會被加入到整個K-means算法過程中
樣本只能歸為一類，不適合多分類任務
k值對K-means影響很大，因為在執行算法之前，並不知道要將樣本分為幾類，k值選擇不恰當，可能會導致模型難以收斂

優點:

對於大數據集，算法時間復雜度為線性 O(NKT) 其中，N: 樣本點個數、K: 聚類中心個數、T: 迭代次數
因為每次迭代更新質心時，需要計算所有樣本點和所有類中心的距離，所以是N·K，要迭代T次，再乘以T
局部最優解通常已經可以滿足問題需要

Kmeans++

前言

前面我們提到過K-means存在一些問題，其中一個問題就是K-means對初始的類中心非常敏感，Kmeans++就是專門對初始值的選擇進行優化的

問題點: 隨機選取k個數據，若數據非常靠近，會導致收斂很慢，甚至收斂到局部最小值
可見聚類的結果高度依賴質心的初始化，所以為了解決初始時如何選取k個類中心點的問題，引入了K-means++算法，它的核心思想是，距離已選中心點越遠，被選為下一個中心點的概率越大
那麼問題來了，那是不是選擇距離所有已選中心點最遠的那個點作為下一個中心點呢？並不是，如果這樣做很容易選到異常的離群點，從而影響最終的聚類效果

輪盤法

在講Kmeans之前，先講一下輪盤賭法，基本上很多文章談到輪盤賭算法，都會和遺傳算法，蟻群算法一起解釋
步驟:

計算出每個群體照顧你每個個體的適應度 f ( i = 1 , 2 , . . . , m ) f(i=1, 2, ..., m) f(i=1,2,...,m)，m為群體大小
計算每個個體被遺傳到下一代群體中的概率 P ( x i ) = f ( x i ) ∑ j = 1 m f ( x j ) P(x_i) = \frac{f(x_i)}{\sum_{j=1}^{m} f(x_j)} P(xi)=∑j=1mf(xj)f(xi)
計算每個個體的累計概率 q ( x i ) = ∑ k = 1 i P ( x k ) q(x_i) = \sum_{k=1}^{i} P(x_k) q(xi)=∑k=1iP(xk)，這樣，如果某個個體的適應度高，則它所對應的個體選擇概率就會越大，通過累計概率轉換後對應的線段就會越長
選擇某個個體策略為在區間[0 1]中隨機產生一個數，看看該數字落在那個區間，很明顯，對於適應度值較大的個體，對應的線段長度會長，這樣隨機產生的數字落在此區間的概率就大，該個體被選中的概率也大。同時，對於適應度較小的個體，線段長度會相對較短，隨機數字在該區間的概率相對較小，但是也有被選中的可能，避免了適應度數值較小的個體被直接淘汰的問題

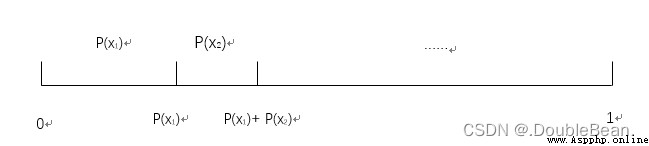
舉例
初始種群適應度為 [169, 576, 64, 361]，那麼每個個體被遺傳到下一代群體的概率為:
P ( x 1 ) = f ( x 1 ) ∑ j = 1 m f ( x j ) = 169 169 + 576 + 64 + 361 = 0.14 P ( x 2 ) = f ( x 2 ) ∑ j = 1 m f ( x j ) = 576 169 + 576 + 64 + 361 = 0.49 P ( x 3 ) = f ( x 3 ) ∑ j = 1 m f ( x j ) = 64 169 + 576 + 64 + 361 = 0.06 P ( x 4 ) = f ( x 4 ) ∑ j = 1 m f ( x j ) = 361 169 + 576 + 64 + 361 = 0.31 P(x_1) = \frac{f(x_1)}{\sum_{j=1}^{m} f(x_j)} = \frac{169}{169 + 576 + 64 + 361} = 0.14 \\ P(x_2) = \frac{f(x_2)}{\sum_{j=1}^{m} f(x_j)} = \frac{576}{169 + 576 + 64 + 361} = 0.49 \\ P(x_3) = \frac{f(x_3)}{\sum_{j=1}^{m} f(x_j)} = \frac{64}{169 + 576 + 64 + 361} = 0.06 \\ P(x_4) = \frac{f(x_4)}{\sum_{j=1}^{m} f(x_j)} = \frac{361}{169 + 576 + 64 + 361} = 0.31 P(x1)=∑j=1mf(xj)f(x1)=169+576+64+361169=0.14P(x2)=∑j=1mf(xj)f(x2)=169+576+64+361576=0.49P(x3)=∑j=1mf(xj)f(x3)=169+576+64+36164=0.06P(x4)=∑j=1mf(xj)f(x4)=169+576+64+361361=0.31
每個個體的累計概率為:
q ( x 1 ) = ∑ j = 1 1 P ( x j ) = 0.14 q ( x 2 ) = ∑ j = 1 2 P ( x j ) = 0.14 + 0.49 = 0.63 q ( x 3 ) = ∑ j = 1 3 P ( x j ) = 0.14 + 0.49 + 0.06 = 0.69 q ( x 4 ) = ∑ j = 1 1 P ( x j ) = 0.14 + 0.9 + 0.06 + 0.31 = 1 q(x_1) = \sum_{j=1}^{1} P(x_j) = 0.14 \\ q(x_2) = \sum_{j=1}^{2} P(x_j) = 0.14 + 0.49 = 0.63 \\ q(x_3) = \sum_{j=1}^{3} P(x_j) = 0.14 + 0.49 + 0.06 = 0.69 \\ q(x_4) = \sum_{j=1}^{1} P(x_j) = 0.14 + 0.9 + 0.06 + 0.31 = 1 q(x1)=j=1∑1P(xj)=0.14q(x2)=j=1∑2P(xj)=0.14+0.49=0.63q(x3)=j=1∑3P(xj)=0.14+0.49+0.06=0.69q(x4)=j=1∑1P(xj)=0.14+0.9+0.06+0.31=1

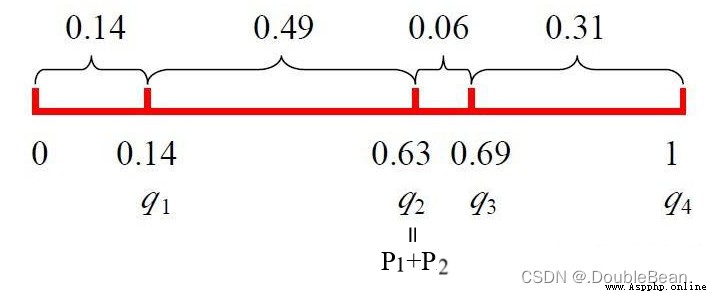
隨機產生一個數r=0.672452，發現是落在[q₂, q₃]之間，則x₃被選中

Kmeans++代碼實現

步驟:

從輸入的數據點集合中隨機選擇一個點作為第一個聚類中心
對於數據集中的每一個點x_i，計算它與當前已有聚類中心之間的最短距離(即與最近的一個聚類中心的距離)，用D(x)表示
選擇一個新的數據點作為新的聚類中心，選擇的原則是：D(x)較大的點，被選取作為聚類中心的概率較大，方法是計算每個樣本被選為下一個聚類中心的概率 D ( x ) 2 ∑ x ∈ X D ( x ) 2 \frac{D(x)^2}{\sum_{x∈X} D(x)^2} ∑x∈XD(x)2D(x)2，然後按照輪盤算法選擇出下一個聚類
重復2、3步驟直到選擇出k個聚類質心
利用這k個質心來作為初始化質心去運行標准的K-Means算法

代碼

class my_Kmeans_plus:
def __init__(self, k, init):
self.k = k
self.init = init # init='random'就是標准Kmeans，init='Kmeans++'就是Kmeans++
# 距離度量函數: 計算任意點之間的距離
def calc_distance(self, vec1, vec2):
return np.sqrt(np.sum(np.power(vec1 - vec2, 2)))
''' 利用輪盤法選擇下一個聚類中心 參數: P是各樣本點被選為下一個聚類中心的概率集合 r是區間[0, 1]之間隨機生成的一個數，判斷該數落在哪個區間，則這個區間被選中 返回的是被選中的樣本索引 '''
def RWS(self, P, r):
q = 0 # 累計概率
for i in range(len(P)):
q += P[i] # P[i]表示第i個樣本被選中的概率
if r <= q: # 產生的隨機數在該區間內
return i
def fit(self, data):
numSamples, dim = data.shape # numSamples指樣本總數，dim指特征維度
if self.init == 'random':
# 隨機並且不重復地選取k個數據作為初始聚類中心點
self.centers_idx = np.random.choice(numSamples, self.k, replace = False) # 得到的是質心點的索引
# 默認類別是從0到k-1
self.centers = data[self.centers_idx].astype(np.float32) # 初始化聚類中心
# print(self.centers)
elif self.init == 'Kmeans++':
first = np.random.choice(numSamples) # 隨機選出一個樣本點作為第一個聚類的中心
index_select = [first] # 將聚類中心索引存儲到一個列表中
D = np.zeros((numSamples, 1)) # 初始化D(x)
# 繼續選取k-1個點
for j in range(1, self.k):
for i in range(numSamples):
D[i] = float('inf')
for idx in index_select:
distance = self.calc_distance(data[i], data[idx])
D[i] = min(D[i], distance)
# 計算概率
P = np.square(D) / np.sum(np.square(D))
r = np.random.random() # r為0到1的隨機數
choiced_index = self.RWS(P, r)
index_select.append(choiced_index) # 利用輪盤法選擇下一個聚類中心
# print(index_select)
self.centers = data[index_select].astype(np.float32)
# print(self.centers)
# ClusterAssment記錄每個樣本的信息: 第一列記錄樣本所屬聚類中心的索引，第2列記錄樣本與聚類中心的距離
ClusterAssment = np.zeros((numSamples, 2))
ClusterChanged = True
while ClusterChanged:
ClusterChanged = False
# 遍歷所有點求每個點與各個聚類中心點的距離
for i in range(numSamples):
mindist = self.calc_distance(data[i], self.centers[0])
label = 0
for j in range(1, self.k):
distance = self.calc_distance(data[i], self.centers[j])
# 把第i個數據分配到距離最近的聚類中心
if distance < mindist:
mindist = distance
label = j
# print("mindist = {}，label = {}".format(mindist, label))
# 判斷樣本所屬聚類中心是否發生了變化，若發生了變化則更新數據
if ClusterAssment[i, 0] != label:
ClusterChanged = True
ClusterAssment[i, :] = label, mindist
# print(ClusterAssment, '\n')
# 對每個類別的樣本重新求聚類中心，並更新聚類中心
for j in range(self.k):
# 找到所有屬於類中心j的樣本數據
pointsInCluster = data[ClusterAssment[:, 0] == j]
# print("{}: {}".format(j, pointsInCluster))
self.centers[j, :] = (np.mean(pointsInCluster, axis=0).tolist()) # 更新聚類中心的位置
def predict(self, data):
numSamples, dim = data.shape
ClusterAssment = np.zeros((numSamples, 2))
for i in range(numSamples):
mindist = self.calc_distance(data[i], self.centers[0])
label_pred = 0
for j in range(1, self.k):
distance = self.calc_distance(data[i], self.centers[j])
if distance < mindist:
mindist = distance
label_pred = j
ClusterAssment[i, :] = label_pred, mindist ** 2
return self.centers, ClusterAssment

調用自己寫的類

# 不調庫實現Kmeans++
model = my_Kmeans_plus(k = 5, init = 'Kmeans++')
model.fit(data)
centers, ClusterAssment = model.predict(data)
''' # 不調庫實現Kmeans model = my_Kmeans_plus(k = 5, init = 'random') model.fit(data) centers, ClusterAssment = model.predict(data) '''
plt.figure(figsize=(6, 5))
plt.scatter(data[:, 0], data[:, 1], c = ClusterAssment[:, 0])
plt.scatter(centers[:, 0], centers[:, 1], marker = '*', color = 'r', s = 100) # 繪制類中心點
plt.show()

模型的穩定性提高了一些

SSE指標

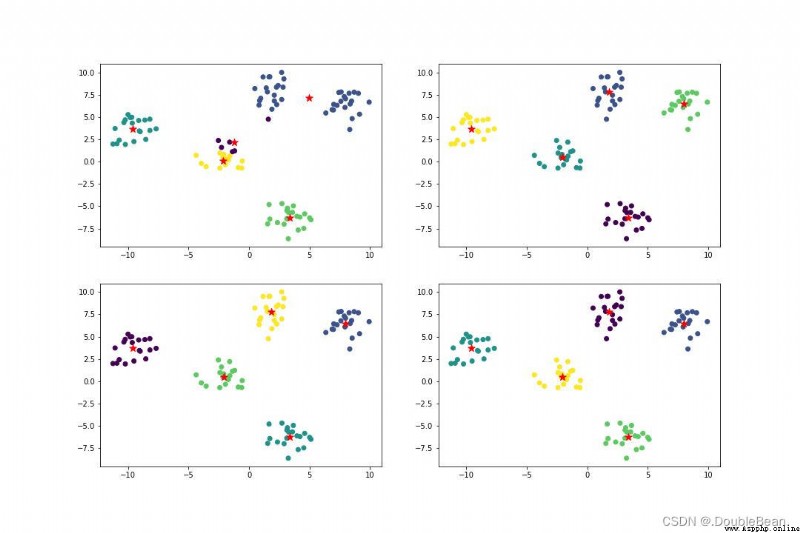
SSE (sum of the squared errors，誤差平方和)
S S E = ∑ i = 1 k ∑ x j ∈ C i d i s t ( x j − μ i ) 2 SSE = \sum_{i=1}^{k} \sum_{x_j ∈ C_i} dist(x_j - μ_i)^2 SSE=i=1∑kxj∈Ci∑dist(xj−μi)2
其中，C_i是第i個類，x_j是C_i中的樣本點，μ_i是C_i的類中心(C_i中所有樣本的均值)，dist是歐幾裡得距離，SSE是所有樣本的聚類誤差，用來評估聚類效果的好壞，可以理解為損失函數

因為我們要考慮如何更好地更新類中心，使得對於所有樣本點，到其所屬類的類中心距離之和最小
m i n S S E = ∑ i = 1 k ∑ x j ∈ C i ( x j − μ i ) 2 = ∑ i = 1 k ∑ x j ∈ C i ( x j T x j − x j T μ i − μ i T x j + μ i T μ i ) = ∑ i = 1 k ( ∑ x j ∈ C i x j T x j − ( ∑ x j ∈ C i x j T ) μ i − μ i T ( ∑ x j ∈ C i x j ) + m i μ i T μ i ) \begin{aligned} min SSE =& \sum_{i=1}^{k} \sum_{x_j ∈ C_i} (x_j - μ_i)^2 \\ =& \sum_{i=1}^{k} \sum_{x_j ∈ C_i} (x_j^Tx_j - x_j^Tμ_i - μ_i^Tx_j + μ_i^Tμ_i) \\ =& \sum_{i=1}^{k} (\sum_{x_j ∈ C_i} x_j^Tx_j - (\sum_{x_j ∈ C_i} x_j^T)μ_i - μ_i^T(\sum_{x_j ∈ C_i} x_j) + m_i μ_i^Tμ_i) \end{aligned} minSSE===i=1∑kxj∈Ci∑(xj−μi)2i=1∑kxj∈Ci∑(xjTxj−xjTμi−μiTxj+μiTμi)i=1∑k(xj∈Ci∑xjTxj−(xj∈Ci∑xjT)μi−μiT(xj∈Ci∑xj)+miμiTμi)
其中，m_i是第i個類中樣本點個數
對類中心求導:
∂ S S E ∂ μ i = − ( ∑ x j ∈ C i x j ) − ( ∑ x j ∈ C i x j ) + 2 m i μ i \frac{\partial SSE}{\partial μ_i} = - (\sum_{x_j ∈ C_i} x_j) - (\sum_{x_j ∈ C_i} x_j) + 2m_iμ_i ∂μi∂SSE=−(xj∈Ci∑xj)−(xj∈Ci∑xj)+2miμi
令 ∂ S S E ∂ μ i = 0 \frac{\partial SSE}{\partial μ_i} = 0 ∂μi∂SSE=0
μ i = 1 m i ∑ x j ∈ C i x j μ_i = \frac{1}{m_i}\sum_{x_j∈C_i} {x_j} μi=mi1xj∈Ci∑xj
由上式可知，類的最小化SSE的最佳類中心點是類中所有樣本點的均值

手肘法

前面提到Kmeans的缺點中，有提到過k值的選取對K-means影響很大。引用的這個數據集可以很容易看出來數據應該劃分為5類，但不是所有數據集都能這麼容易得出k值的大小，一種選取k值的辦法就是通過不斷嘗試: 手肘法

手肘法的核心指標便是SSE

如圖所示便是該數據的肘部曲線圖，橫坐標是k值的選取，縱坐標是誤差平方和，曲線呈現遞降的趨勢，為什麼？
當k=1時，表示不對樣本點進行分類，直接認為所有樣本點為同一類。當 k = numSamples，即k為樣本點的個數，就是一個樣本點分為一類，每一個類的類中心就是樣本點自己本身，所以樣本點到自己的類中心的距離都為0，SSE就為0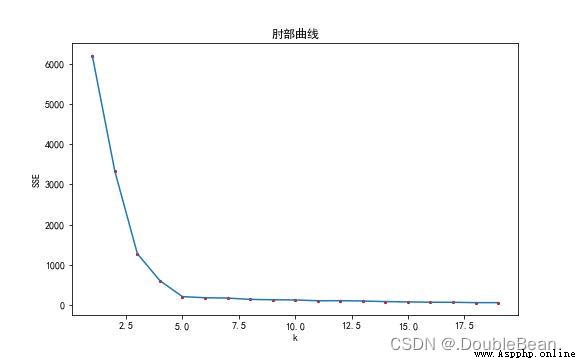

手肘法的核心思想是：隨著聚類數k的增大，樣本劃分會更加精細，每個簇的聚合程度會逐漸提高，那麼誤差平方和SSE自然會逐漸變小。並且，當k小於真實聚類數時，由於k的增大會大幅增加每個簇的聚合程度，故SSE的下降幅度會很大，而當k到達真實聚類數時，再增加k所得到的聚合程度回報會迅速變小，所以SSE的下降幅度會驟減，然後隨著k值的繼續增大而趨於平緩，也就是說SSE和k的關系圖是一個手肘的形狀，而這個肘部對應的k值就是數據的真實聚類數。當然，這也是該方法被稱為手肘法的原因

手肘法可視化代碼實現

from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
# 畫肘部法曲線
K = []
inertia = []
for k_num in range(20): # 這裡按理說應該是data.shape[0]，但數據的樣本點太多，而且也沒必要
model = my_Kmeans_plus(k = k_num + 1, init = 'Kmeans++')
model.fit(data)
centers, ClusterAssment = model.predict(data)
K.append(k_num + 1)
inertia.append(np.sum(ClusterAssment[:, 1]))
plt.title('肘部曲線')
plt.xlabel('k')
plt.ylabel('SSE')
plt.plot(K, inertia)
plt.scatter(K, inertia, c='r', s=4)
plt.show()

調庫實現Kmeans並繪制手肘法

from sklearn.cluster import KMeans
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
sse = []
for k_num in range(1, 20):
model = KMeans(n_clusters=k_num, init="random", n_init=10, max_iter=200)
model.fit(data)
sse.append(model.inertia_)
plt.title('肘部曲線')
plt.xlabel('k')
plt.ylabel('SSE')
plt.plot(range(1, 20), sse)
plt.scatter(range(1, 20), sse, c='r', s=4)
plt.show()