您现在的位置：程式師世界 >> 編程語言 > >> 更多編程語言 >> Python

Talking about the K-means algorithm and implementation (based on Python)

編輯：Python

Kmeans可視化
https://www.naftaliharris.com/blog/visualizing-k-means-clustering/

K-means原理

K-means 有一個著名的解釋：牧師—村民模型：

有四個牧師去郊區布道,一開始牧師們隨意選了幾個布道點,並且把這幾個布道點的情況公告給了郊區所有的村民,於是每個村民到離自己家最近的布道點去聽課.
聽課之後,大家覺得距離太遠了,於是每個牧師統計了一下自己的課上所有的村民的地址,搬到了所有地址的中心地帶,並且在海報上更新了自己的布道點的位置.
牧師每一次移動不可能離所有人都更近,有的人發現A牧師移動以後自己還不如去B牧師處聽課更近,So each villager went to the nearest mission point……
就這樣,牧師每個禮拜更新自己的位置,村民根據自己的情況選擇布道點,最終穩定了下來

Kmeans,An Unsupervised Clustering Algorithm,It is also the most classic partition-based clustering method.,思想是: 對於給定的樣本集,按照樣本之間的距離大小,將樣本集劃分為K個類.Make the points in the class as close as possible,And make the distance between classes as large as possible
步驟:

First determine the number of dataset classesk
數據預處理: 剔除離群點(Eliminate those that may be caused by human factors,Sample points that are not real data)、數據歸一化(消除量綱的影響,轉換方法為: (X - min) / (max - min) )、數據標准化(Convert the collected data distribution to a standard normal distribution,轉換公式: X減去均值,再除以標准差)
在數據集中隨機選取k個數據,作為初始質心
Calculate the Euclidean distance from each sample in the dataset to each centroid,Divide the samples into the category of the centroid with the smallest distance
根據聚類結果,重新計算質心,Use the mean method to update: μ i = 1 m i ∑ x j ∈ C i x j μ_i = \frac{1}{m_i}\sum_{x_j∈C_i} {x_j} μi=mi1∑xj∈Cixj 其中,C_i是第i個類,x_j是C_i中的樣本點,μ_i是第iA class of center,m_i是第inumber of sample points in a class (Note that the new centroids are not necessarily the actual sample points),When the calculation of the center of mass and centroid are exactly the same last time（或者收斂）時,停止迭代;Otherwise update the centroid,重復執行3、4兩步操作
Considering that the proximity measure is Euclidean distance,使用誤差的平方和(SSE指標),good or bad as a measure of clustering quality,後面再講

例子: https://www.bilibili.com/video/BV1py4y1r7DN?share_source=copy_web
有以下6個點,將A3和A4作為初始質心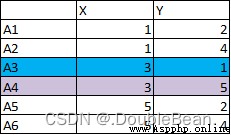

1.Calculate the distance from each point to the centroid,Classify points that are close together.從下圖可以看到A1與A3的距離是2.24,與A4的距離是3.61,所以A1被歸為A3這一類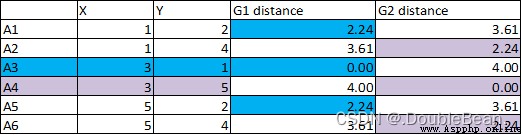

2.place each point in blue,and purple of each pointx,yValues are averaged separately.get new centroids

3.Calculate the new distance each point to the center of mass,Classify points that are close together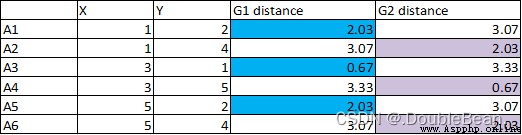

4.Since the connection point has not changed,So the result of the calculation after that will not change,停止計算
5.藍色類: A1, A3, A5.紫色類：A2, A4, A6.

代碼實現

# 不調庫實現
class my_Kmeans:
def __init__(self, k):
self.k = k
# 距離度量函數: Calculate the distance between arbitrary points
def calc_distance(self, vec1, vec2):
return np.sqrt(np.sum(np.power(vec1 - vec2, 2)))
def fit(self, data):
numSamples, dim = data.shape # numSamplesRefers to the total number of samples,dim指特征維度
# Random and non-repetitive selectionkdata as the initial cluster center point
self.centers_idx = np.random.choice(numSamples, self.k, replace=False) # What is obtained is the index of the centroid point
self.centers = data[self.centers_idx].astype(np.float32) # 初始化聚類中心
# ClusterAssmentRecord information for each sample: The first column records the index of the cluster center to which the sample belongs,第2The column records the square of the distance between the sample and the cluster center(用於SSE指標)
ClusterAssment = np.zeros((numSamples, 2))
ClusterChanged = True
while ClusterChanged:
ClusterChanged = False
# Iterate through all the points for each point and each cluster center distance
for i in range(numSamples):
mindist = self.calc_distance(data[i], self.centers[0])
label = 0
for j in range(1, self.k):
distance = self.calc_distance(data[i], self.centers[j])
# 把第idata is assigned to the nearest cluster center
if distance < mindist:
mindist = distance
label = j
# print("mindist = {},label = {}".format(mindist, label))
# Determine whether the cluster center to which the sample belongs has changed,Update the data if there is a change
if ClusterAssment[i, 0] != label:
ClusterChanged = True
ClusterAssment[i, :] = label, mindist ** 2
# print(ClusterAssment, '\n')
# Recalculate the cluster center for each class of samples,並更新聚類中心
for j in range(self.k):
# Find all that belong to the class centerj的樣本數據
pointsInCluster = data[ClusterAssment[:, 0] == j]
# print("{}: {}".format(j, pointsInCluster))
self.centers[j, :] = (np.mean(pointsInCluster, axis=0).tolist()) # Update the location of the cluster center
def predict(self, data):
numSamples, dim = data.shape
ClusterAssment = np.zeros((numSamples, 2))
for i in range(numSamples):
mindist = self.calc_distance(data[i], self.centers[0])
label_pred = 0
for j in range(1, self.k):
distance = self.calc_distance(data[i], self.centers[j])
if distance < mindist:
mindist = distance
label_pred = j
ClusterAssment[i, :] = label_pred, mindist ** 2
return self.centers, ClusterAssment

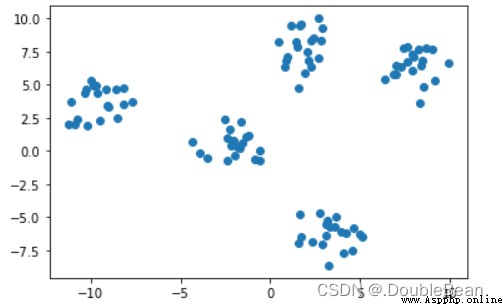
generate some datasets,來檢驗Kmeans聚類效果

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_blobs
data, true_labels = make_blobs(centers = 5, random_state = 20, cluster_std = 1) # datais the set of coordinates,ture_labels是正確標簽
plt.scatter(data[:, 0], data[:, 1])
plt.show()

# 不調庫實現
model = my_Kmeans(k=5)
model.fit(data)
''' model.fit()函數返回值 centers: 聚類中心坐標 ClusterAssment: Information for each sample: The first column records the index of the cluster center to which the sample belongs,第2The column records the square of the distance between the sample and the cluster center(用於SSE指標) '''
centers, ClusterAssment = model.predict(data)
plt.figure(figsize=(6, 5))
plt.scatter(data[:, 0], data[:, 1], c = ClusterAssment[:, 0])
plt.scatter(centers[:, 0], centers[:, 1], marker = '*', color = 'r', s = 100) # draw class center point
plt.show()

The following figure is the result of the code running,After running it several times, you will find that the library is not adjusted.KmeansClustering results will vary,That is, it is implemented without calling the libraryKmeansThe result is a local optimum in most cases,並非全局最優

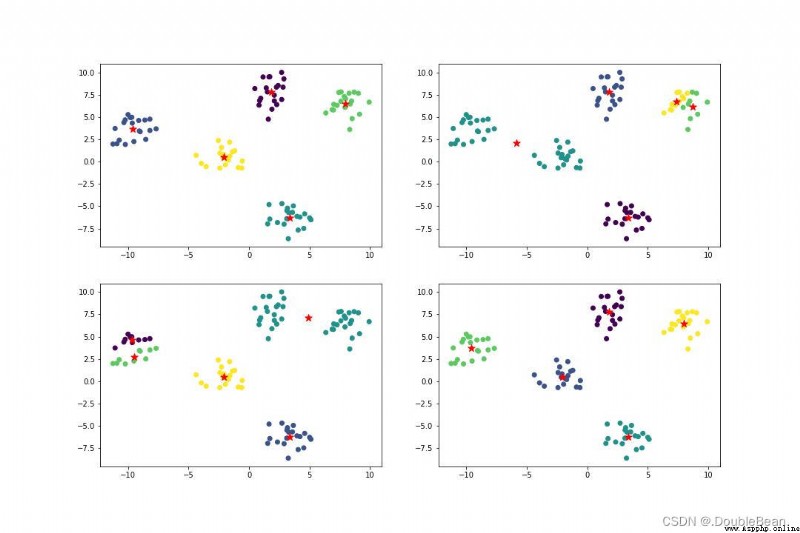
If the library is implemented,無論運行多少次,結果都很好

# 調庫實現
from sklearn.cluster import KMeans
model_1 = KMeans(n_clusters=5)
label_pred_1 = model_1.fit_predict(data)
plt.figure(figsize=(6, 5))
plt.scatter(data[:, 0], data[:, 1], c = label_pred_1)
plt.show()

缺點:

sensitive to initial class centers,步驟2Randomly select data as initial centroids,可以想象,When the distance between the centroids is very close,will need to iterate many times,will affect the convergence speed,And it is possible that you end up with only local minima
步驟3中計算距離,我們應該想到,Distance is affected by dimension,在使用時,Need to think about normalization;And because it is applied to all samples,Therefore, it will be more sensitive to abnormal data.,Very sensitive to outlier data,A small amount of noisy data can make a big difference to the average,所以穩定性較差
Q: The data preprocessing part will not have to cut out the outliers？Why is it still affected by outliers?？
A: Some outliers are easy to identify,But some outliers are not easy to judge,For example, outliers are on the edge of the data distribution,We don't know if it's real data or an outlier,So there are still outliers that will be added to the entireK-means算法過程中
樣本只能歸為一類,不適合多分類任務
k值對K-means影響很大,because before the algorithm is executed,do not know how to divide the samples into categories,kInappropriate value choice,May cause the model to be difficult to converge

優點:

對於大數據集,Algorithm time complexity is linear O(NKT) 其中,N: 樣本點個數、K: 聚類中心個數、T: 迭代次數
Because each iteration updates the centroid,Need to calculate the distance of all sample points and all class centers,所以是N·K,要迭代T次,再乘以T
局部最優解通常已經可以滿足問題需要

Kmeans++

前言

前面我們提到過K-means存在一些問題,其中一個問題就是K-meansVery sensitive to initial class centers,Kmeans++It is specially optimized for the selection of initial values.

問題點: 隨機選取k個數據,If the data is very close,will lead to slow convergence,even converges to a local minimum
The result of visible clustering is highly dependent on the initialization of the centroids,So in order to solve the initial selectionkThe center of a class of problems,引入了K-means++算法,它的核心思想是,The farther from the selected center point,The greater the probability of being selected as the next center point
那麼問題來了,Does that select the point farthest from all the selected center points as the next center point?？並不是,If you do this it is easy to pick abnormal outliers,Thus affecting the final clustering effect

輪盤法

在講Kmeans之前,Let's talk about roulette,Basically a lot of articles talk about the roulette algorithm,Metropolis and Genetic Algorithms,Ant colony algorithm explained together
步驟:

Calculate the fitness of each group to take care of each individual of you f ( i = 1 , 2 , . . . , m ) f(i=1, 2, ..., m) f(i=1,2,...,m),m為群體大小
Calculate the probability that each individual will be inherited into the next generation of the population P ( x i ) = f ( x i ) ∑ j = 1 m f ( x j ) P(x_i) = \frac{f(x_i)}{\sum_{j=1}^{m} f(x_j)} P(xi)=∑j=1mf(xj)f(xi)
Calculate the cumulative probability for each individual q ( x i ) = ∑ k = 1 i P ( x k ) q(x_i) = \sum_{k=1}^{i} P(x_k) q(xi)=∑k=1iP(xk),這樣,If an individual's fitness is high,It corresponds to the individual selection probability of will,The converted by the cumulative probability corresponding line segment will be longer
Choose an individual strategy to be in the interval[0 1]randomly generate a number,See where the number falls in that range,很明顯,For individuals with larger fitness values,The corresponding line segment length will be longer,In this way, the probability of randomly generated numbers falling within this range is high.,The individual has a high probability of being selected.同時,For individuals with less fitness,Line segment length will be relatively short,The probability of a random number being in this interval is relatively small,But there is also the possibility of being selected,Avoid the problem of individuals with smaller fitness values being directly eliminated

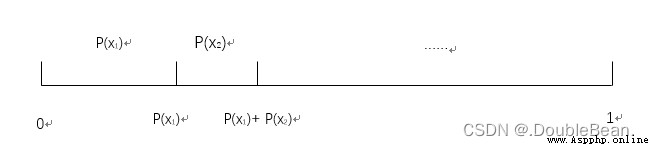
舉例
The initial population fitness is [169, 576, 64, 361],Then the probability of each individual being inherited to the next generation is:
P ( x 1 ) = f ( x 1 ) ∑ j = 1 m f ( x j ) = 169 169 + 576 + 64 + 361 = 0.14 P ( x 2 ) = f ( x 2 ) ∑ j = 1 m f ( x j ) = 576 169 + 576 + 64 + 361 = 0.49 P ( x 3 ) = f ( x 3 ) ∑ j = 1 m f ( x j ) = 64 169 + 576 + 64 + 361 = 0.06 P ( x 4 ) = f ( x 4 ) ∑ j = 1 m f ( x j ) = 361 169 + 576 + 64 + 361 = 0.31 P(x_1) = \frac{f(x_1)}{\sum_{j=1}^{m} f(x_j)} = \frac{169}{169 + 576 + 64 + 361} = 0.14 \\ P(x_2) = \frac{f(x_2)}{\sum_{j=1}^{m} f(x_j)} = \frac{576}{169 + 576 + 64 + 361} = 0.49 \\ P(x_3) = \frac{f(x_3)}{\sum_{j=1}^{m} f(x_j)} = \frac{64}{169 + 576 + 64 + 361} = 0.06 \\ P(x_4) = \frac{f(x_4)}{\sum_{j=1}^{m} f(x_j)} = \frac{361}{169 + 576 + 64 + 361} = 0.31 P(x1)=∑j=1mf(xj)f(x1)=169+576+64+361169=0.14P(x2)=∑j=1mf(xj)f(x2)=169+576+64+361576=0.49P(x3)=∑j=1mf(xj)f(x3)=169+576+64+36164=0.06P(x4)=∑j=1mf(xj)f(x4)=169+576+64+361361=0.31
The cumulative probability of each individual is:
q ( x 1 ) = ∑ j = 1 1 P ( x j ) = 0.14 q ( x 2 ) = ∑ j = 1 2 P ( x j ) = 0.14 + 0.49 = 0.63 q ( x 3 ) = ∑ j = 1 3 P ( x j ) = 0.14 + 0.49 + 0.06 = 0.69 q ( x 4 ) = ∑ j = 1 1 P ( x j ) = 0.14 + 0.9 + 0.06 + 0.31 = 1 q(x_1) = \sum_{j=1}^{1} P(x_j) = 0.14 \\ q(x_2) = \sum_{j=1}^{2} P(x_j) = 0.14 + 0.49 = 0.63 \\ q(x_3) = \sum_{j=1}^{3} P(x_j) = 0.14 + 0.49 + 0.06 = 0.69 \\ q(x_4) = \sum_{j=1}^{1} P(x_j) = 0.14 + 0.9 + 0.06 + 0.31 = 1 q(x1)=j=1∑1P(xj)=0.14q(x2)=j=1∑2P(xj)=0.14+0.49=0.63q(x3)=j=1∑3P(xj)=0.14+0.49+0.06=0.69q(x4)=j=1∑1P(xj)=0.14+0.9+0.06+0.31=1

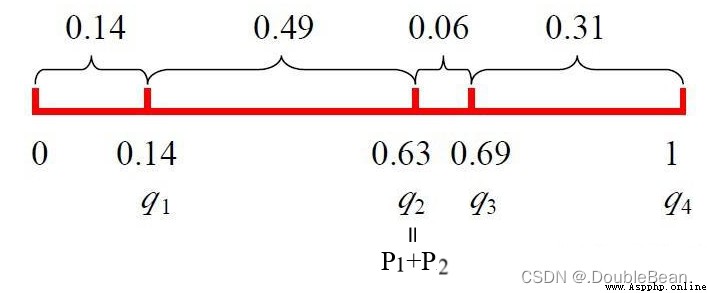
隨機產生一個數r=0.672452,found to fall[q₂, q₃]之間,則x₃被選中

Kmeans++代碼實現

步驟:

從輸入的數據點集合中隨機選擇一個點作為第一個聚類中心
對於數據集中的每一個點x_i,Calculate the shortest distance between it and the currently existing cluster center(That is, the distance to the nearest cluster center),用D(x)表示
選擇一個新的數據點作為新的聚類中心,選擇的原則是：D(x)較大的點,被選取作為聚類中心的概率較大,The method is to calculate the probability that each sample is selected as the next cluster center D ( x ) 2 ∑ x ∈ X D ( x ) 2 \frac{D(x)^2}{\sum_{x∈X} D(x)^2} ∑x∈XD(x)2D(x)2,Then select the next cluster according to the roulette algorithm
重復2、3steps until selectedk個聚類質心
利用這k個質心來作為初始化質心去運行標准的K-Means算法

代碼

class my_Kmeans_plus:
def __init__(self, k, init):
self.k = k
self.init = init # init='random'就是標准Kmeans,init='Kmeans++'就是Kmeans++
# 距離度量函數: Calculate the distance between arbitrary points
def calc_distance(self, vec1, vec2):
return np.sqrt(np.sum(np.power(vec1 - vec2, 2)))
''' Select the next cluster center using the roulette method 參數: Pis the probability set that each sample point is selected as the next cluster center r是區間[0, 1]a randomly generated number between,Determine which range the number falls in,then this interval is selected Returns the index of the selected sample '''
def RWS(self, P, r):
q = 0 # 累計概率
for i in range(len(P)):
q += P[i] # P[i]表示第i個樣本被選中的概率
if r <= q: # The random number generated is within the interval
return i
def fit(self, data):
numSamples, dim = data.shape # numSamplesRefers to the total number of samples,dim指特征維度
if self.init == 'random':
# Random and non-repetitive selectionkdata as the initial cluster center point
self.centers_idx = np.random.choice(numSamples, self.k, replace = False) # What is obtained is the index of the centroid point
# The default category is from0到k-1
self.centers = data[self.centers_idx].astype(np.float32) # 初始化聚類中心
# print(self.centers)
elif self.init == 'Kmeans++':
first = np.random.choice(numSamples) # Randomly select a sample point as the center of the first cluster
index_select = [first] # Store cluster center indices into a list
D = np.zeros((numSamples, 1)) # 初始化D(x)
# 繼續選取k-1個點
for j in range(1, self.k):
for i in range(numSamples):
D[i] = float('inf')
for idx in index_select:
distance = self.calc_distance(data[i], data[idx])
D[i] = min(D[i], distance)
# 計算概率
P = np.square(D) / np.sum(np.square(D))
r = np.random.random() # r為0到1的隨機數
choiced_index = self.RWS(P, r)
index_select.append(choiced_index) # Select the next cluster center using the roulette method
# print(index_select)
self.centers = data[index_select].astype(np.float32)
# print(self.centers)
# ClusterAssmentRecord information for each sample: The first column records the index of the cluster center to which the sample belongs,第2The column records the distance between the sample and the cluster center
ClusterAssment = np.zeros((numSamples, 2))
ClusterChanged = True
while ClusterChanged:
ClusterChanged = False
# Iterate through all the points for each point and each cluster center distance
for i in range(numSamples):
mindist = self.calc_distance(data[i], self.centers[0])
label = 0
for j in range(1, self.k):
distance = self.calc_distance(data[i], self.centers[j])
# 把第idata is assigned to the nearest cluster center
if distance < mindist:
mindist = distance
label = j
# print("mindist = {},label = {}".format(mindist, label))
# Determine whether the cluster center to which the sample belongs has changed,Update the data if there is a change
if ClusterAssment[i, 0] != label:
ClusterChanged = True
ClusterAssment[i, :] = label, mindist
# print(ClusterAssment, '\n')
# Recalculate the cluster center for each class of samples,並更新聚類中心
for j in range(self.k):
# Find all that belong to the class centerj的樣本數據
pointsInCluster = data[ClusterAssment[:, 0] == j]
# print("{}: {}".format(j, pointsInCluster))
self.centers[j, :] = (np.mean(pointsInCluster, axis=0).tolist()) # Update the location of the cluster center
def predict(self, data):
numSamples, dim = data.shape
ClusterAssment = np.zeros((numSamples, 2))
for i in range(numSamples):
mindist = self.calc_distance(data[i], self.centers[0])
label_pred = 0
for j in range(1, self.k):
distance = self.calc_distance(data[i], self.centers[j])
if distance < mindist:
mindist = distance
label_pred = j
ClusterAssment[i, :] = label_pred, mindist ** 2
return self.centers, ClusterAssment

調用自己寫的類

# 不調庫實現Kmeans++
model = my_Kmeans_plus(k = 5, init = 'Kmeans++')
model.fit(data)
centers, ClusterAssment = model.predict(data)
''' # 不調庫實現Kmeans model = my_Kmeans_plus(k = 5, init = 'random') model.fit(data) centers, ClusterAssment = model.predict(data) '''
plt.figure(figsize=(6, 5))
plt.scatter(data[:, 0], data[:, 1], c = ClusterAssment[:, 0])
plt.scatter(centers[:, 0], centers[:, 1], marker = '*', color = 'r', s = 100) # draw class center point
plt.show()

The stability of the model has been improved a bit

SSE指標

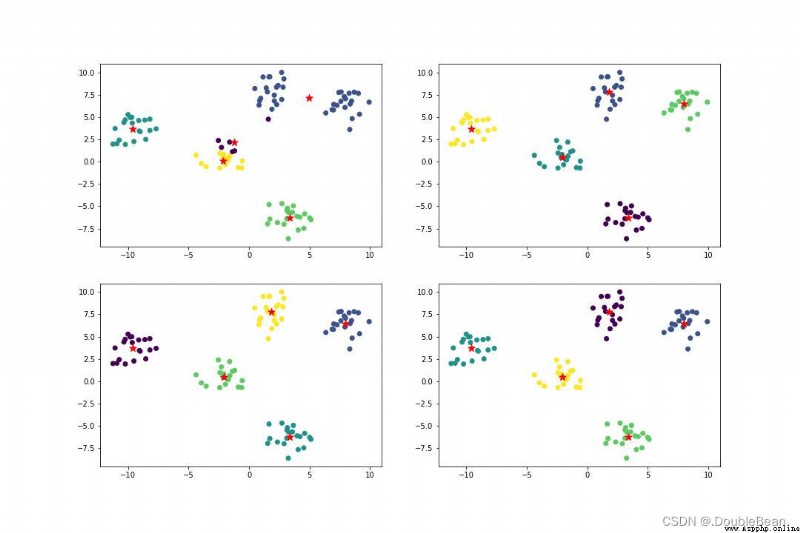
SSE (sum of the squared errors,誤差平方和)
S S E = ∑ i = 1 k ∑ x j ∈ C i d i s t ( x j − μ i ) 2 SSE = \sum_{i=1}^{k} \sum_{x_j ∈ C_i} dist(x_j - μ_i)^2 SSE=i=1∑kxj∈Ci∑dist(xj−μi)2
其中,C_i是第i個類,x_j是C_i中的樣本點,μ_i是C_i的類中心(C_i中所有樣本的均值),dist是歐幾裡得距離,SSE是所有樣本的聚類誤差,It is used to evaluate the quality of clustering effect,可以理解為損失函數

Because we have to consider how to better update the class center,so that for all sample points,The sum of the distances to the class centers of the class to which it belongs is the smallest
m i n S S E = ∑ i = 1 k ∑ x j ∈ C i ( x j − μ i ) 2 = ∑ i = 1 k ∑ x j ∈ C i ( x j T x j − x j T μ i − μ i T x j + μ i T μ i ) = ∑ i = 1 k ( ∑ x j ∈ C i x j T x j − ( ∑ x j ∈ C i x j T ) μ i − μ i T ( ∑ x j ∈ C i x j ) + m i μ i T μ i ) \begin{aligned} min SSE =& \sum_{i=1}^{k} \sum_{x_j ∈ C_i} (x_j - μ_i)^2 \\ =& \sum_{i=1}^{k} \sum_{x_j ∈ C_i} (x_j^Tx_j - x_j^Tμ_i - μ_i^Tx_j + μ_i^Tμ_i) \\ =& \sum_{i=1}^{k} (\sum_{x_j ∈ C_i} x_j^Tx_j - (\sum_{x_j ∈ C_i} x_j^T)μ_i - μ_i^T(\sum_{x_j ∈ C_i} x_j) + m_i μ_i^Tμ_i) \end{aligned} minSSE===i=1∑kxj∈Ci∑(xj−μi)2i=1∑kxj∈Ci∑(xjTxj−xjTμi−μiTxj+μiTμi)i=1∑k(xj∈Ci∑xjTxj−(xj∈Ci∑xjT)μi−μiT(xj∈Ci∑xj)+miμiTμi)
其中,m_i是第iThe number of sample points in each class
Derivation to Class Center:
∂ S S E ∂ μ i = − ( ∑ x j ∈ C i x j ) − ( ∑ x j ∈ C i x j ) + 2 m i μ i \frac{\partial SSE}{\partial μ_i} = - (\sum_{x_j ∈ C_i} x_j) - (\sum_{x_j ∈ C_i} x_j) + 2m_iμ_i ∂μi∂SSE=−(xj∈Ci∑xj)−(xj∈Ci∑xj)+2miμi
令 ∂ S S E ∂ μ i = 0 \frac{\partial SSE}{\partial μ_i} = 0 ∂μi∂SSE=0
μ i = 1 m i ∑ x j ∈ C i x j μ_i = \frac{1}{m_i}\sum_{x_j∈C_i} {x_j} μi=mi1xj∈Ci∑xj
由上式可知,class minimizationSSEThe best all the sample points in the center of class is the class average

手肘法

前面提到Kmeans的缺點中,有提到過k值的選取對K-means影響很大.The referenced dataset makes it easy to see that the data should be divided into5類,But not all datasets are so easy to derivek值的大小,a choicekThe only way to get value is to keep trying: 手肘法

The core indicator of the elbow method isSSE

As shown in the figure is the elbow curve of the data,橫坐標是k值的選取,The ordinate is the error sum of squares,The curve shows a decreasing trend,為什麼？
當k=1時,Say not to classify sample points,Directly consider all sample points to be of the same class.當 k = numSamples,即k為樣本點的個數,Is a sample points are divided into category,The class center of each class is the sample point itself,So the center of the sample point to their class distance are for0,SSE就為0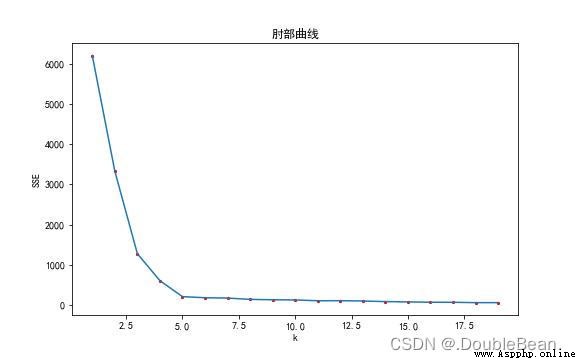

手肘法的核心思想是：隨著聚類數k的增大,樣本劃分會更加精細,每個簇的聚合程度會逐漸提高,那麼誤差平方和SSE自然會逐漸變小.並且,當k小於真實聚類數時,由於k的增大會大幅增加每個簇的聚合程度,故SSE的下降幅度會很大,而當k到達真實聚類數時,再增加k所得到的聚合程度回報會迅速變小,所以SSE的下降幅度會驟減,然後隨著k值的繼續增大而趨於平緩,也就是說SSE和k的關系圖是一個手肘的形狀,而這個肘部對應的k值就是數據的真實聚類數.當然,這也是該方法被稱為手肘法的原因

Elbow method visualization code implementation

from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
# Draw Elbow Curve
K = []
inertia = []
for k_num in range(20): # Here it should bedata.shape[0],But there are too many sample points in the data,而且也沒必要
model = my_Kmeans_plus(k = k_num + 1, init = 'Kmeans++')
model.fit(data)
centers, ClusterAssment = model.predict(data)
K.append(k_num + 1)
inertia.append(np.sum(ClusterAssment[:, 1]))
plt.title('elbow curve')
plt.xlabel('k')
plt.ylabel('SSE')
plt.plot(K, inertia)
plt.scatter(K, inertia, c='r', s=4)
plt.show()

調庫實現Kmeansand draw the elbow method

from sklearn.cluster import KMeans
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
sse = []
for k_num in range(1, 20):
model = KMeans(n_clusters=k_num, init="random", n_init=10, max_iter=200)
model.fit(data)
sse.append(model.inertia_)
plt.title('elbow curve')
plt.xlabel('k')
plt.ylabel('SSE')
plt.plot(range(1, 20), sse)
plt.scatter(range(1, 20), sse, c='r', s=4)
plt.show()