聲明：本文為學習筆記，侵權刪

一、一些基本概念

K-Means是非監督學習的聚類算法，將一組數據分為K類（或者叫簇/cluster），每個簇有一個質心（centroid），同類的數據是圍繞著質心被分類的。數據被分為了幾類就有幾個質心。

算法步驟：

1、先從原始數據集中隨機選出K個數據，作為K個質心。

2、將剩余的數據分配到與之最相似的的質心的那個簇裡。

3、第一次分類完成後，計算每個簇內樣本的均值，並根據這個均值生成新的質心

4、重復2,3步，直至質心的變化距離小於某個值（主觀設定），如果質心始終沒法穩定下來，也可以設定一個最大迭代次數，即使質心仍不穩定一樣會跳出循環。

解釋：

如何判斷數據間的相似性？

K-Means算法判斷數據間的相似性的標准是歐氏距離（可以簡單理解為中學裡學的點到點之間的距離公式）。每個數據可以看做一個點，一個數據可以由多個維度組成（比如能不能考研上岸可以由：智商、努力、運氣決定，智商、努力、運氣都可以量化成數字，於是可以想象X軸是智商，Y軸是努力，Z軸是運氣，這樣能否考研上岸就可以變成三維坐標裡的一個點了）。OK，現在數據變成坐標系裡的點了，就可以計算歐氏距離了。歐氏距離越小，兩個數據點越相似。

怎麼計算每個簇內樣本的均值？

每個軸上的數據分別算平均值，然後生成一個新的點：X軸的數據算平均值，Y軸的數據算平均值以此類推。新點的坐標：(mean(X),mean(Y),mean(Z)...)

如何判斷結果的優劣？

這裡主要討論簇內誤差平方和（SSE），簡單來說：SSE=一個簇內所有點到質心的距離之和。SSE越小，效果通常更好。當然，SSE不能作為唯一的判定標准，因為SSE只考慮了簇內樣本的相關性，並未考慮簇與簇之間的相關性。同時如果K值設定得過大，分了太多的簇，一個簇裡總共沒幾個樣本，那SSE當然就更小，但這並不代表分類效果更好。

同一組數據重復多次K-Means算法，做出來的結果是一樣的嗎？

不是，因為初始的質心是隨即的，所以最終結果會有一定的隨機性，但大體上是一樣的。

二、實踐

回憶一下之前做RFM分類中，將用戶分為8大類。RFM分類有一個缺陷就是：分類的標准是主觀的，因此對分類標准很難做到客觀准確。而使用K-Means就會彌補這個缺陷。

這裡用的數據集還是做RFM的那個。

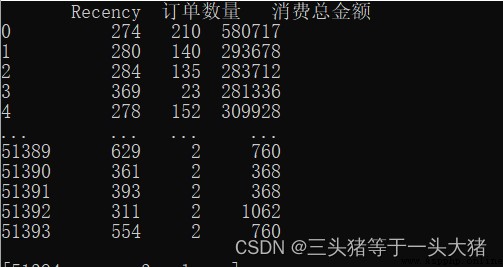
 在使用K-Means的時候，還是選擇R（最近一次消費至今的時間間隔）,F（消費次數）,M（消費總金額）三組數據最為用戶分類的指標。

三組數據如下：

 產生一個問題

R,F,M作為坐標點，描述一個數據點，但是在K-Means中要計算數據點之間的距離來判斷不同數據點的相似性。如果用原數據（如上圖），計算距離的時候，M（消費總金額）對距離的影響太大了，進而導致模型效果不好（因為M數值很大，在計算數據點之間的歐式距離的時候，F,M在其中的作用就微乎其微，這是不理想的。舉個例子：用戶A只消費了1次，且消費時間距今20天，但金額巨大，有100萬；用戶B消費了100次，且最近一次消費距今5天，消費總金額也很大，共99萬。計算A,B的相似性的時候，幾乎只有M在起作用，因此可能就把A,B分為一類的，但很明顯，A是暴發戶，B是回頭客，明顯不是一類人嘛）。為了消除某個數據特別大/特別小而影響模型，我們需要對數據標准化處理（Normalization）。

數據標准化：把范圍較大的數據限制到一個某一特定區間內。最常見的也是本例中用的標准化方法就是將值限制到均值為0，方差為1的正態分布中：  。好處有很多，就不一一贅述了。

#normalization
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
x_normalization = scaler.fit_transform(x)
x_df = pd.DataFrame(x_normalization,columns=x.columns,index=x.index)
print(x_normalization)
print(x_df)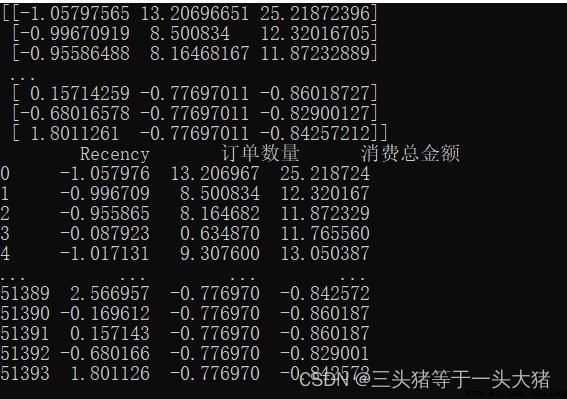

 很明顯，通過數據標准化，各項數值之間的差距變小了很多，因此模型也能更好得訓練。

搭建K-Means模型並訓練：

先按著之前做RFM模型的預想，將用戶分為8類：

from sklearn.cluster import KMeans
KMeans_model = KMeans(n_clusters=8,random_state = 1)
KMeans_model.fit(x_normalization)
#質心
print(KMeans_model.cluster_centers_)
#每個樣本的標簽
print(KMeans_model.labels_)
#SSE
print(KMeans_model.inertia_)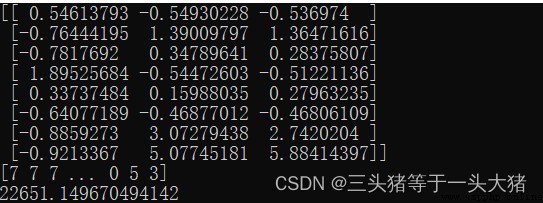

二維數組表示8個質心的坐標（R,F,M）。

一維數組表示每個樣本被分到了哪一類

最後的22651表示SSE

從RFM的角度來說，這樣就分類成功了。但又有一個問題：

真的需要分成8類嗎？是不是分的太細了？

這麼問了，當然是不需要分為8類的，但為什麼呢？因為：在做K-Means的時候，需要遵從肘部法則。

肘部法則

肘部法則：在K-Means算法的時候，取不同的K值，計算出對應的SSE，繪制折線圖，會出現一個K值K_，當K<K_時，SSE下降幅度很大，K≥K_時，SSE的下降幅度趨於平緩。

意義：SSE下降很大時，說明新增的每一個類對降低SSE都有顯著效果，也就是說，新增的這個類是必要的。反之，則說明新增的類沒啥大用了。

我們可以畫出本例中，K取不同值時候的SSE的變化情況：

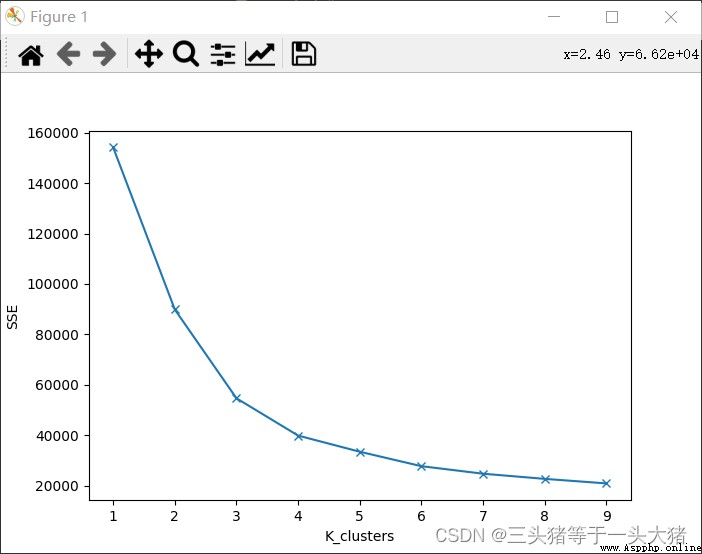
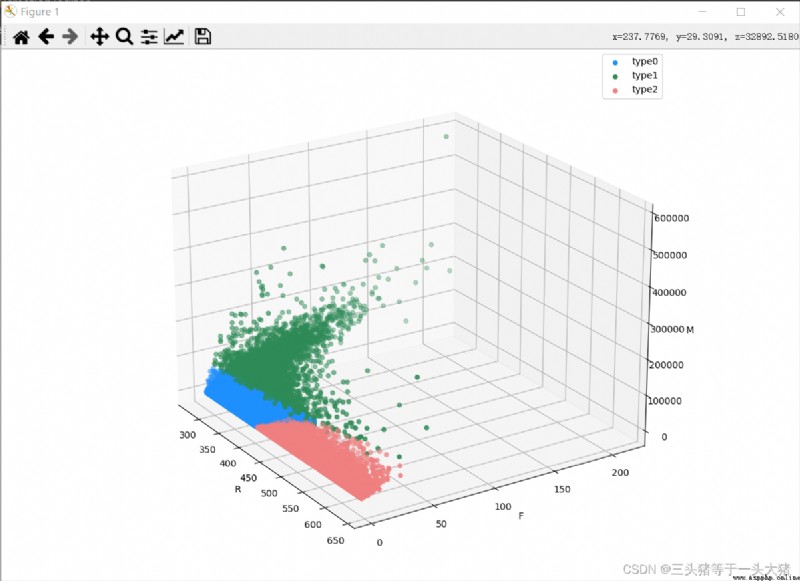
 從上圖中可以看到，K≥4的時候（分成4類及以上的時候），SSE的下降已經不明顯了，而K<3的時候SSE下降明顯，因此選用K=3訓練模型，並畫出對應的3D散點圖.

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
labels = KMeans_model.labels_
fig = plt.figure()
ax = Axes3D(fig)
color = ["dodgerblue", "seagreen", "lightcoral"]
for i in range(3):
#獲取分到的類是類i的所有數據
d = x[labels == i]
ax.scatter(d["Recency"], d["訂單數量"], d["消費總金額"], color=color[i], label=f"type{i}")
ax.set_xlabel("R")
ax.set_ylabel("F")
ax.set_zlabel("M")
# 使用plt.legend()函數展示圖例
plt.legend()
# 展示圖像
plt.show()