# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
import os
import pandas as pd
def moranI(W, X):
''' W:空間權重矩陣 X:觀測值矩陣 歸一化空間權重矩陣後進行moran檢驗,實例https://bbs.pinggu.org/thread-3568074-1-1.html '''
#W=W.astype(float)
W = np.array(W)
X = np.array(X)
X = X.reshape(1, -1)
W = W / W.sum(axis=1) # 歸一化
n = W.shape[0] # 空間單元數
Z = X - X.mean() # 離差陣
S0 = W.sum()
S1 = 0
for i in range(n):
for j in range(n):
S1 += 0.5 * (W[i, j] + W[j, i]) ** 2
S2 = 0
for i in range(n):
S2 += (W[i, :].sum() + W[:, i].sum()) ** 2
# 全局moran指數
I = np.dot(Z, W)
I = np.dot(I, Z.T)
I = n / S0 * I / np.dot(Z, Z.T)
# 在正太分布假設下的檢驗數
EI_N = -1 / (n - 1)
VARI_N = (n ** 2 * S1 - n * S2 + 3 * S0 ** 2) / (S0 ** 2 * (n ** 2 - 1)) - EI_N ** 2
ZI_N = (I - EI_N) / (VARI_N ** 0.5)
# 在隨機分布假設下檢驗數
EI_R = -1 / (n - 1)
b2 = 0
for i in range(n):
b2 += n * Z[0, i] ** 4
b2 = b2 / ((Z * Z).sum() ** 2)
VARI_R = n * ((n ** 2 - 3 * n + 3) * S1 - n * S2 + 3 * S0 ** 2) - b2 * (
(n ** 2 - n) * S1 - 2 * n * S2 + 6 * S0 ** 2)
VARI_R = VARI_R / (S0 ** 2 * (n - 1) * (n - 2) * (n - 3)) - EI_R ** 2
ZI_R = (I - EI_R) / (VARI_R ** 0.5)
# 計算局部moran指數
Ii = list()
for i in range(n):
Ii_ = n * Z[0, i]
Ii__ = 0
for j in range(n):
Ii__ += W[i, j] * Z[0, j]
Ii_ = Ii_ * Ii__ / ((Z * Z).sum())
Ii.append(Ii_)
Ii = np.array(Ii)
# 局部檢驗數
ZIi = list()
EIi = Ii.mean()
VARIi = Ii.var()
for i in range(n):
ZIi_ = (Ii[i] - EIi) / (VARIi ** 0.5)
ZIi.append(ZIi_)
ZIi = np.array(ZIi)
''' # moran散點圖 # 用來正常顯示中文標簽 plt.rcParams['font.sans-serif'] = ['SimHei'] # 用來正常顯示負號 plt.rcParams['axes.unicode_minus'] = False fig = plt.figure() ax = fig.add_subplot(1, 1, 1) ax.spines['top'].set_color('none') ax.spines['right'].set_color('none') ax.xaxis.set_ticks_position('bottom') ax.spines['bottom'].set_position(('data', 0)) ax.yaxis.set_ticks_position('left') ax.spines['left'].set_position(('data', 0)) WZ = np.dot(Z, W) ax.scatter(Z, WZ, c='k') x1 = range(int(Z.min()), int(Z.max() + 1)) y1 = range(int(Z.min()), int(Z.max() + 1)) ax.plot(x1, y1, 'k--', label='x=y') x2 = list(range(int(Z.min()), int(Z.max() + 1))) y2 = np.array(x2) * I[0][0] ax.plot(x2, y2, 'k-', label='I*x=y') ax.legend(loc='upper right') imgPath = os.path.join(os.getcwd(), '莫蘭散點圖.png') ax.set_title('莫蘭散點圖') fig.savefig(imgPath) '''
return {
'I': {
'value': I[0, 0], 'desc': '全局moran指數'},
'ZI_N': {
'value': ZI_N[0, 0], 'desc': '正太分布假設下檢驗數'},
'ZI_R': {
'value': ZI_R[0, 0], 'desc': '隨機分布假設下檢驗數'},
'Ii': {
'value': Ii, 'desc': '局部moran指數'},
'ZIi': {
'value': ZIi, 'desc': '局部檢驗數'},
#'img': {'path': imgPath, 'desc': '莫蘭散點圖路徑'}
}
if __name__ == "__main__":
df = pd.read_csv('adj.csv',header=None,index_col=None)
w=np.array(df)
df1=pd.read_csv('attribute.csv',header=None,index_col=None)
x = np.array(df1)
print(len(data),len(x[0]))
result=moranI(w, x)
print(result['I'],result['ZI_N'])
運行結果如下:
{
'value': 0.18758732033404646, 'desc': '全局moran指數'} {
'value': 31.11189591476361, 'desc': '正太分布假設下檢驗數'}
matlab求解全局莫蘭指數:
①文件名為moransi.m
②直接調用傳入參數即可
function global_moran_test(x0,w)
row = size(x0,2);
moran.mean = zeros(row,1);
moran.num = zeros(row,1);
moran.stdev = zeros(row,1);
moran.index = zeros(row,1);
moran.z = zeros(row,1);
moran.p = zeros(row,1);
moran.globalresult = zeros(row,3);
for r = 1 : 1 : row
x = x0(:,r);
moran.mean(r) = mean(x);
moran.num(r) = size(x,1);
moran.stdev(r) = std(x);
z_x = (x - moran.mean(r)) / moran.stdev(r);
sum_wij = 0;
s = 0;
s1 = 0;
s2 = 0;
m2 = 0;
m4 = 0;
for a = 1 : 1 : moran.num(r)
w_i = 0;
w_j = 0;
m2 = m2 + (x(a,1) - moran.mean(r))^2;
m4 = m4 + (x(a,1) - moran.mean(r))^4;
for b = 1 : 1 : moran.num(r)
sum_wij = sum_wij + (w(a,b) * z_x(a,1) * z_x(b,1));
s = s + w(a,b);
s1 = s1 + (w(a,b) + w(b,a))^2;
w_i = w_i + w(a,b);
w_j = w_j + w(b,a);
end
s2 = s2 + (w_i + w_j)^2;
end
m2 = m2 / moran.num(r);
m4 = m4 / moran.num(r);
b2 = m4 / (m2^2);
sum_i2 = 0;
for a = 1 : 1 : moran.num(r)
sum_i2 = sum_i2 + (z_x(a,1) * z_x(a,1));
end
moran.index(r) = (moran.num(r) * sum_wij) / (s * sum_i2);
n = moran.num(r);
temp_1 = n * (n^2 - 3 * n + 3) * s1 - (n * s2) + (3 * s^2);
temp_2 = b2 * ((n^2 - n) * s1 - (2 * n * s2) + (6 * s^2));
den = (n - 1) * (n - 2) * (n - 3) * (s^2);
sd = (temp_1 - temp_2) / den - (1 / (n-1))^2;
sd = sqrt(sd);
e = -1 / (n - 1);
moran.z(r) = (moran.index(r) - e) / sd;
moran.p(r) = 1 - normcdf(moran.z(r));
end
moran.globalresult(:,1) = moran.index;
moran.globalresult(:,2) = moran.z;
moran.globalresult(:,3) = moran.p;
fprintf('%6s %12s %18s %24s\r\n','t','Moran','z','p');
for i = 1 : 1 : row
fprintf('%6.3f %12.3f %18.3f %24.3\n',i,moran.index(i),moran.z(i),moran.p(i));
end
end
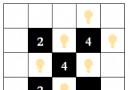 Solution to the problems of pythonb group of the 13th National tournament of the Blue Bridge Cup
Solution to the problems of pythonb group of the 13th National tournament of the Blue Bridge Cup
The 13th National tournament o
 Computer graduation design Python+django train ticketing system (source code + system + mysql database + Lw document)
Computer graduation design Python+django train ticketing system (source code + system + mysql database + Lw document)
Project IntroductionWith the r