做一個問答系統,根據輸入的內容,提出的問題,得到一個答案。詳細見下面數據集的介紹。
前期采用的數據集是英文的,因為中文數據集少,而且訓練數據量太小。使用的是Facebook 的公共數據The (20) QA bAbI tasks,官方下載鏈接如下:https://research.fb.com/downloads/babi/
此數據集包含20個任務,每種任務相似但又有些許差異。每種任務包含10,000多對問答對,每個問答對可以分成三部分:內容、問題和答案。內容可以是一個句子、幾個句子或者一個段落一篇文章。問題是一個句子。答案是一個單詞或者一個詞組,並且答案一定是在內容中出現的。以下為一種數據集中一個樣本的表現形式:
可見輸入內容是三個句子,問題是一個句子,答案為一個單詞。其中答案多數情況下不是根據一個句子直接產生的,而是需要通過多個句子相互推理得出。以上為最簡單的問答對,內容只有2句,有些任務的內容可能多達80句,對模型的推理能力要求更高。推理的邏輯難度也有很大的差異,有些只需要推理一次,相互推理的句子間隔很小,有些問答對的答案需要根據多個句子推理,句子和句子之間間隔很大,因此如何捕獲句子間的關系,並保留有效信息是個難點。(數字1叫做支持句子編號,即答案是根據哪些編號的句子按順序推理出來的,此次的模型不會使用到該部分信息。)以下為難度較大的例子:
可見輸入的句子個數明顯增加,需要句子間的推理,並且需要推理的句子之間間隔了多個無效句子。
模型的設計思路來自多篇論文,鏈接和介紹如下:
DMN作為此次模型的基本模型,此後的改動都在其基礎之上。以下詳細介紹Dynamic Memory Network (DMN) 模型:
DMN由4部分組成,分別叫做輸入模塊(Input Module),問題模塊(Question Module),事件記憶模塊(Episodic Memory Module),回答模塊(Answer Module)
在介紹模型之前,先對RNNs做基本的介紹,熟悉可跳過:
RNN可以看做每層網絡結點有連接的神經網絡。網絡會對前面的信息進行記憶並應用於當前輸出的計算中,即上一層隱藏層的輸出會作為當前隱藏層輸入的一部分,因此可以認為當前隱藏層輸出的狀態包含了前面所有詞向量的信息。
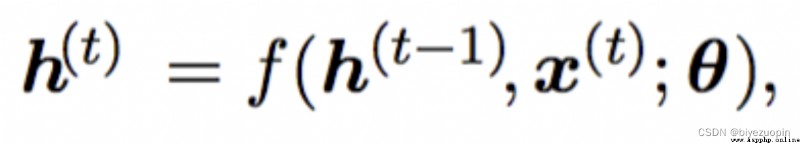
表示當前隱藏層的輸出,h(t-1)表示上一時刻的隱藏層輸出,x(t)表示當前時刻的輸入詞向量(代表當前單詞的詞向量),為函數所需要的參數(為矩陣)。可以理解為h(t)包含了前面所有單詞的信息。具體的計算過程如下式所示:
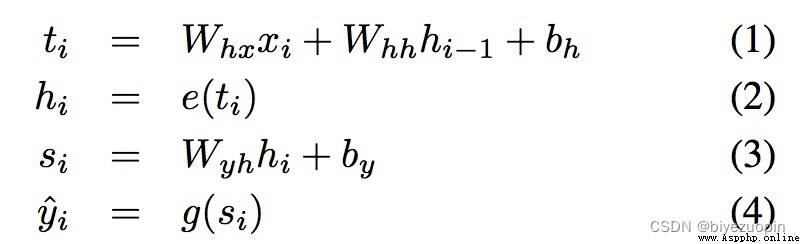
Whx , Whh , Wyh , bh , by就是之前的,分別代表三個權重參數和偏置參數。e和g代表預定義好的非線性函數。
GRU為RNN的改進版,能夠解決梯度消失的問題,因此能夠更好的保留輸入信息。
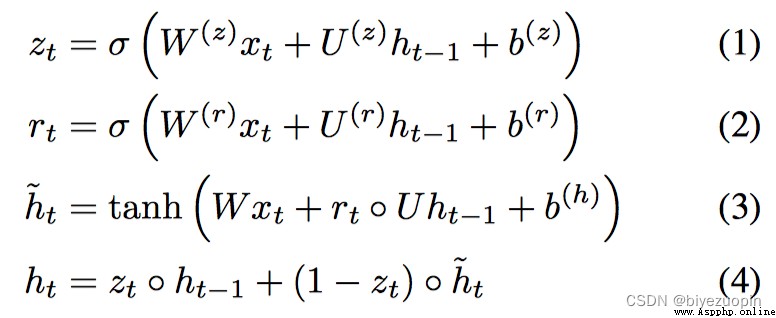
上式為GRU的計算公式,相比於傳統的RNN,隱藏層輸出的計算新增了兩個參數zt , rt ,分別代表更新門(Update Gate)和重置門(Reset Gate)以及
t的重要性有多大。除此之外,GRU不存在memory的概念,而是簡單的上一時刻的隱藏狀態全部用作當前時刻的輸入。
由此可見,GRU結構通過更新門和重置門對傳入下一層網絡的權重加以控制,結構上比傳統RNN更復雜,也因此能更好的解決長句子信息消失的問題。而LSTM相比於GRU又多了一層控制:設置一個參數控制上一個時間點的隱藏層狀態對當前隱藏層狀態的影響權重。
除此之外,還引入了雙向RNN的結構。以上所說的情況,當前的隱藏層狀態只受之前的隱藏,可以理解為由前向後的傳播。雙向結構引入了由後向前的傳播,使當前隱藏層狀態不但受之前的影響,也受到未來時刻的影響,使信息的傳播更為充分。此外,RNN還能設置為多層結構,根據需求取最後一層的狀態或對每層狀態加權最為最後的隱藏層狀態。
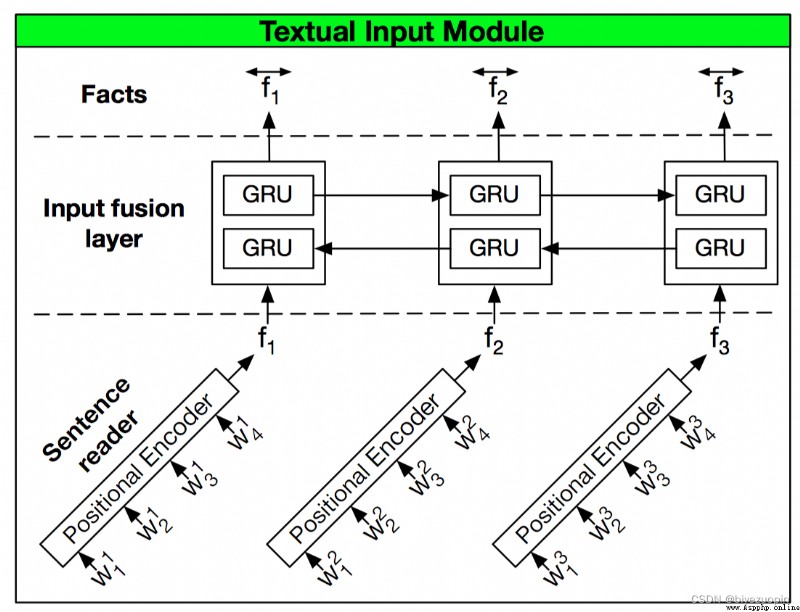
做的工作是把輸入的文本(在此數據集中為多個句子的集合)轉換為向量表達式。
現在每個句子都是由若干個單詞組成的,首先使用詞嵌入層(Word Embedding)把單詞轉換為二維的張量(Tensor,GPU計算時支持的一種數據結構,可以理解為list。)假設單詞個數為8,詞嵌入層指定的詞向量維度為80,那麼句子進過詞嵌入層後的輸出即為 8 * 80的二維Tensor。(此時暫時不考慮Batch Size的使用,此步驟是為了加快訓練過程。若使用,輸出為Batch size * 8 * 80的三維Tensor)然後把此二維Tensor輸入Recurrent Neural Network (RNN),目前有多種RNN結構的變體,比如常見的LSTM,GRU等。LSTM的結構較GRU復雜,DMN的作者證明使用GRU能夠得到和LSTM相近的效果,所以采用單向GRU即可。
因此,輸入模塊的輸出即為GRU的輸出,在不考慮batch size的情況下,當輸入為一句話時,輸出是個二維的Tensor,其中保留了對句子中所有單詞的信息總結。當輸入的句子是多個句子時,先對多個句子進行拼接,在每個句子尾部增加句末標識符,最後輸出標識符處的隱藏層狀態進行拼接。以下分析使用batch size時Tensor的維度:
在訓練過程中引入batch size是為了加快計算,能夠每次訓練多個問答對,因此通常都會引入batch size。因為GRU的輸入為Tensor格式,所以對於不同長度的句子以及句子個數不同的batch需要進行padding,通常的做法是在有效信息後面補0.
假設batch size為2,詞向量維度為80,padding後每個contexts最多的句子個數為6.那麼GRU的輸入是:代表輸入內容的2 * 6 * 80的tensor和代表初始隱藏層的2 * 2 * 80 Tensor,第二個維度的2是因為雙向GRU。GRU的輸出也是兩部分,分別代表cell和hidden。Cell 儲存每次GRU迭代的隱藏層狀態,維度為2 * 6 * 160,第三個維度是因為考慮了雙向GRU。hidden代表最後一次隱藏層的狀態,維度為 2 * 2 * 80,第二個維度是因為考慮了雙向GRU。我們把cell分成兩個2 * 6 * 80的tensor相加最後輸入模塊的輸出。
問題模塊的特點是輸入只可能是一個句子,采用的結構和輸入模塊相同,是輸入模塊句子個數為一的情況。問題模塊的輸出也被用作Episodic Memory Module中memory的初始狀態。對應的Tensor維度為 1 * 2 * 80 (句子個數batch size詞向量維度)

把Episodic Memory Module的輸出和Question Module的輸出拼接成 2*160的Tensor。使用交叉熵損失函數作為loss進行反向傳播訓練。預測字典中每個單詞的概率,把最大概率的單詞作為結果。
以上為該問答系統的基模型,大致流程可用下圖表示。
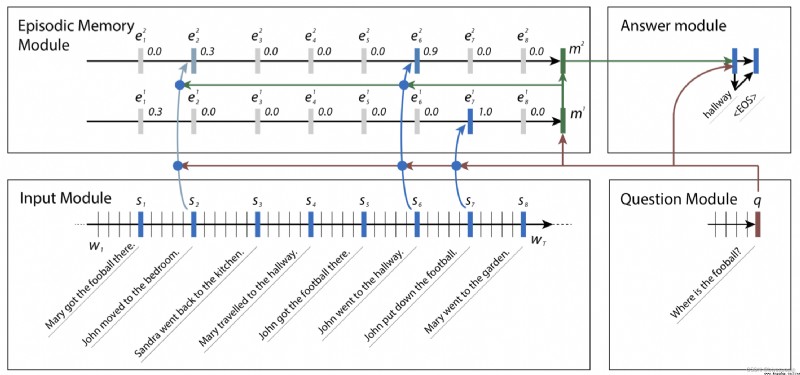
可見Input Module把每個句子編碼成S1至S8的向量並流入Episodic Memory Module,結合Question Module的向量形式輸入,不斷的自我迭代更新每個句子的權重,忽略權重值接近0的句子,最後把關注點放在了S2和S6。把最後生成的memory作為Answer Module的輸入生成答案。
DMN模型在實際表現中存在多方面的問題。首先,其Input Module采用的是單向GRU,每個時刻的隱藏層狀態包含了之前句子(單詞)的總結,卻沒有考慮後面句子的信息。此外,當句子個數很多或句子很長時,讓最後一個時刻的隱藏狀態包含前面所有句子(單詞)的信息很困難,容易導致信息丟失的問題。因此需要對Input Module改進。其次,在Attention Mechanism中計算GRU的update gate zt
對當前的隱藏層狀態帶來影響)時,只考慮了來自上個時刻隱藏層和當前輸入的影響,沒有考慮問題和之前memory可能帶來的影響。最後,在Memory Update Mechanism中,之前是根據輸入模塊的輸出ct,上一時刻的隱藏層狀態ht-1作為GRU的輸入更新當前時刻隱藏層狀態。這就意味著每次迭代隱藏層狀態的權重是一樣的,這樣的模型被稱為tied model,表現能力受限。
對於Input Module的改進:
首先引入一個叫做位置編碼(positional encoding)的結構,把之前從單詞層面的編碼轉換成句子層面的編碼。因為問題總是跟句子相關,在句子層面上的建模顯得更加合理。相當於用positional encoding代替之前的GRU結構,一方面降低了計算量,另一方面又捕獲了單詞位置的關系。具體的做法是對句子中每個單詞的詞向量根據其所在的位置乘以一個權重,最後把所有的詞向量相加形成的Tensor代表對整個句子的信息歸納。positional encoding的計算規則(即詞向量權重)如下:
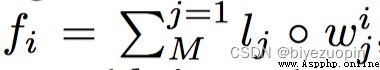
ljd為M*D的二維列表,M表示一個問答對中的句子個數,D表示最長的句子中單詞個數。此外j為句子的索引,d為句子中單詞的索引。隨後將該二維列表和詞向量點乘,並對每個句子中的詞向量求和作為positional encoding結構的輸出。
得到的Tensor維度應為 句子個數*詞向量維度。
在此之後,引入Input Fusion Layer使句子之間的信息能夠交互,本質上是雙向GRU。

Input Fusion Layer實際做的是把一個context中的多個句子依次進入雙向GRU,把每個時刻的隱藏層狀態拼接作為輸出。保證輸入和輸出的維度未發生改變。
對Attention Mechanism的改進:
首先我們改變z函數,之前的z函數由如下六部分組成,
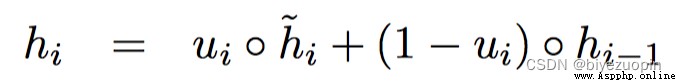
但是實驗發現,只需保留如下四部分,
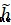
能夠在降低計算量的基礎上得到近似的准確率。
其次,改變Attention Mechanism中GRU的結構,得到名為Attention Based GRU結構。GRU中計算當前隱藏層狀態的公式如下:
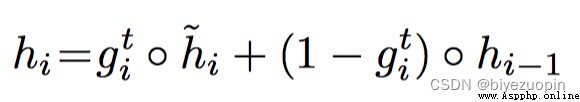
可見ht-1是update gate ui , 上一時刻的隱藏層狀態 hi-1 和代表對當前輸入和上一個時刻隱藏狀態的總結的函數。
Attention Based GRU中計算當前隱藏層狀態的公式如下:
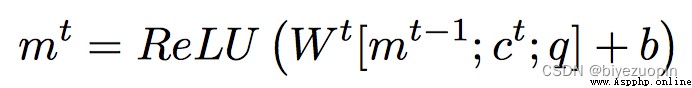
唯一的區別是用attention gate gti替換update gate ui,gti為Attention Mechanism的輸出,代表每個句子的權重(即重要程度),其中還包含了question的信息。
對Memory Update Mechanism的改進:
用RELU函數代替GRU對Memory進行更新:
其中的Memory mt在GRU結構中就是t時刻的隱藏層狀態。c和q為輸入和問題模塊的輸出。通過這樣的改變,能帶來准確率0.5%的提升。
此次的更新在是對Input Module的Positional Encoding。我們使用TreeLSTM代替Positional Encoding。原因是Positional Encoding雖然包含了單詞位置信息,但是TreeLSTM能夠保留單詞間的依賴關系。理論上,最後隱藏層中所包含的信息更多。
首先介紹TreeLSTM結構,TreeLSTM是基於樹的結構使用LSTM,從葉子結點開始不斷迭代,最後把根結點的隱藏狀態作為整個句子的總結。如果我們把TreeLSTM定義為一個類,那麼其執行函數的輸入為代表某個句子的樹對象和代表每個單詞的詞向量形式Tensor. 可見我們需要得到代表句子的樹結構。在這裡使用的是 The Stanford Parser, 介紹和下載路徑如下:
https://nlp.stanford.edu/software/lex-parser.shtml
它能夠把一個句子解析為Dependency Tree(依存樹) 或者 constituency Tree (組成樹)。對於依賴樹而言,每個樹結點是一個單詞,根據本文一開始提到的論文Dependency Parser ,它依靠神經網絡找到單詞和單詞之前的依賴關系,每個結點的孩子必定是和該結點單詞聯系最緊密的幾個單詞,最後聯系強的單詞作為一個詞組形成一個子樹。舉個很簡單的例子 I eat food. 最後的依存樹根結點為eat,I 和 food 分別為eat 的兩個孩子。最終用這棵樹代表整個句子,需要注意的是,每個結點的孩子個數是不固定的。而對於組成樹而言,其每個葉子節點為句子中的單詞,因此葉子結點的個數即為句子中單詞的個數。每個非葉子結點代表多個單詞組成的詞組,最終的結果一個是課二叉樹。還是用上面的例子,最終的樹結構是:I eat food .這個詞組代表根結點(稱為結點0),其左孩子是I eat food (稱為結點1)右孩子是 . (稱為結點2)。對於結點1而言,其左孩子為 I (稱為結點3),右孩子為 eat food (稱為結點4)。而結點4的兩個孩子分別為 eat 和 food。在這裡,我們使用依存樹作為TreeLSTM的樹結構。
此時TreeLSTM的自我迭代不再依賴句子中單詞所在的位置,當前時刻的迭代是以其孩子結點的輸出作為輸入。那麼最後root不僅僅包含了句子中每個單詞的信息,還能夠捕獲單詞之前的結構關系信息。
通過最後實驗證明,在多數任務中,該模型的測試集准確率要優於上個模型的測試集准確率。但在個別任務上(task3, task16),該模型的訓練訓練准確率不如上一個模型。
此時的另一個問題是訓練速度慢,因為對每個句子使用TreeLSTM結構迭代的時候,每一次只能對一個句子迭代,沒有實現batch size。將在下一個模型的更新實現。
該部分主要由陳俏均完成。
在TreeLSTM-DMN+的基礎上引入批處理技術,使得訓練速度加快,但是理論上不會改變模型在測試集上的准確率。我們根據其contexts中句子的數量分批,使得每個批次中contexts的大小保持基本一致。每次取該批次下的batch size個contexts進入TreeLSTM。
由於每個context中每句話的樹結構可能不同,所以無法直接對輸入TreeLSTM模塊的數據直接升維(在現有維度上增加batch size維度)。因此,我們的想法是先記錄下一個批次中所有的樹結點信息。信息包括結點類型是孩子結點還是葉節點,以及該結點的深度,孩子結點的個數,結點編號。最終進入TreeLSTM的結點必定是同一深度,並且擁有相同孩子樹的孩子結點,把這個最為實現批處理的最大批次。
和DMN+模型相比,那些在DMN+中取得100%准確率的任務,在TreeLSTM_DMN+中同樣能取得100%的准確率,在其余任務中,除了在task3和task16表現弱於DMN+,其余任務的准確率都超過了DMN+模型的表現。而在task3和task16中表現較差的原因很有可能是input module的依存樹出現過擬合現象,因為實現中發現,如果控制樹的復雜度,能帶來准確率上的提高,但是仍然弱於DMN+的表現。