利用 A 算法解決八數碼問題,比較不同啟發函數(h1,h2)的搜索效率,並驗證關於 A 算法的命題。
本實驗主要使用 A*算法解決八數碼問題。
八數碼問題主要是由 8 個 1-8 的數字以及一個空格組成一個九宮格,通過移動空格若干次使得九宮格中數字到達以下目標狀態:
對於每個狀態,可以往不同方向移動空格使得該狀態產生多個不同的新狀態作為後繼節點,於是對於候選狀態的選擇策略可以有 BFS、DFS、啟發式搜索等。對於八數碼問題,我們可以理解成一種路徑搜索問題,以其實狀態為起點,目標狀態為終點,進行搜索。每個節點的可搜索路徑為其空格往四個(或更少)方向移動後得到的、不屬於其前驅節點的狀態。
A 算法即對於候選節點每個節點 n,有 f(n),根據 f(n)排序並選擇最優者。其中 f(n)定義為
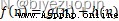
其中 g(n)為起始狀態到 n 的距離,h(n)為 n 到目標狀態的預估距離。
若進一步規定 h(n)≥0,並且定義:
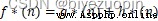
其中,f*(n)表示起點經過 n 到終點的最優路徑搜索費;g*(n)表示起點到 n 的實際最小費用;h*(n)表示 n 到終點的實際最小費用的估計。
當要求 h(n)≤h*(n),就稱這種 A 算法為 A*算法。
A*算法解決八數碼問題的主要流程如下:
設 S0 為起始狀態,Sg 為目標狀態:
Open={ S0}
Closed={}
如果 Open={},失敗退出
在 Open 表中取出其末尾元素 n,n 放到 Closed 表中
若 n∈Sg,則成功退出。
產生 n 的一切非 n 前驅節點的後繼,並構成集合 M。
對 M 中的元素 P,分別作兩類處理:
若 P G(G=Open+Closed),說明 P 並未被搜索到過,則將其計算 f(n),並將其插入 Open 表的合適位置,維護 Open 表從大到小的順序,並將其加入 G 表中。(這裡 f(n)=g(n)+h(n),根據不同 h(n)有不同的啟發式函數,不同的搜索策略)
若 P∈G,說明 P 已經是別的節點的後序節點,則比較從 n 到 P 以及從 P.father 到 P 的消耗,並決定是否更改 P.father轉第三步
在我的代碼中,用一個類保存一個狀態,每個狀態包括一個節點的九宮格信息以及其父節點的指針。即,Tree 的信息跟每個節點的狀態存儲在一個對象中。
在算法退出後,保存最後得到的目標狀態,一路根據其 node.father 追溯到根節點(起始狀態),再逆序,即可得到路徑。
使用的 f(n)中 h1(n)為九宮格中格子與數字不對應的個數,h2(n)為九宮格中每個格子中數字到正確位置需要消耗(橫向縱向移動次數總和),即曼哈頓距離之和。比較兩者 Open 表長度和到達目標的步數。
運行環境為 windows10,Intel Core i5-8400 2.81GHz,RAM 2667MHz 16GB
編譯器 PyCharm,語言 Python3
利用 A*算法求解八數碼問題,在輸出界面上動態顯示 OPEN 表的結點數和評估函值最小的結點
比較兩種啟發函數(上課和書上講到的 h1(n)和 h2(n))的搜索效率,在輸出界面上動態顯示 OPEN 表的結點數、總擴展的結點數和評估函值最小的結點
輸出 OPEN 表中在最佳路徑上的結點及其評估函數值。
先使用課本上的樣例進行測試:
觀察上表可以看到,h2(n)可以迭代更少次數,而且 Open 表和 G 表講更短。
隨機選取了 5 個可行測例,比較 h1(n)與 h2(n)的效率:
可以很清晰比較到兩者的差距,具有更多信息的 h2 的將更快搜索到目標。
驗證凡 A 算法挑選出來求後繼的點 n 必定滿足: f(n)≤f(S0):
f*(S0)表示實際最小費用,用
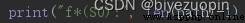
路徑長-1 表示。(len(path)表示路徑經過的點,減 1 後則為路徑邊的個數)
隨機三個可行測例進行三個測試(使用 h2(n))
驗證 h1(n)的單調性,顯示凡 A*算法挑選出來求後繼的點 ni 擴展的一個子結點 nj,檢查是否滿足: h(ni)≤1+h(nj):

這裡使用了課本上的測例,隨機測例由於步數過多無法寫進報告。因此對於隨機測例,我在添加了如下代碼:
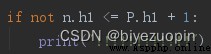
對於每個擴展的 P(即 nj)作判斷,若有違反命題的則打印。結果沒有打印。
如果將空格看作 0,即九數碼問題,利用相似的啟發函數 h1(n)和 h2(n),求解相同的問題的搜索圖是否相同?
不一樣。
當初始起點如左圖
把空格看作 0,h1(n)需要迭代步數 6882,h2(n)需要迭代步數 1352而空格不算入 h1(n)和 h2(n)的話,h1(n)需要迭代步數 6507,h2(n)需要迭代步數 1246每次迭代都要取節點並擴展,因此搜索圖將是不一樣的。
同時它也不是一個 A 算法。假設從目標狀態回退一步(即 0 往任意方向與鄰居交換),得到的狀態的 h1(n)與 h2(n)都是 2,但實際其與目標的距離都是 1,違反了 h(n)<=h(n)的規則。
寫出能否達到目標狀態的判斷方法
將 3*3 的格子以行為順序排列成一行數組 A。
對於 A 中每個數字 n,定義 f(n)為 A 中數字 n 前面比 n 小的數字的個數。定義 SUM 為 f(1)到 f(8)的總和。
我們可以驗證 SUM 的奇偶性將一直保持不變:
當空格左右移動,所有 f(n)都保持不變,SUM 不變
當空格向上移動(設與 n 交換),則在數組 A 中介於空格和 n 中的數有 2 個,記為 a, b。
當空格向下移動,同理可以發現 SUM 永遠以 2 為單位加減變化,其奇偶性不變,因此起點的奇偶性與終點的奇偶性需一樣,這是可達的必要條件。
然而其充分性,我沒有能力證明。
實際上應該使用 numpy 等提升數組操作的速率,然而發現這點時代碼已經成型不方便改動。或者使用 Java,因為該項目不太需要作圖。