該項目主要是利用局部搜索算法(LS)和模擬退火算法(SA)解決 TSP 問題。先是使用 LS 求解 TSP 問題,再嘗試 SA 問題,比較兩者,在效率上 SA 更占有。最後再在 LS 的基礎上使用 SA,再優化 SA 部分算法,嘗試求解 TSP 問題。選用的 TSP 測例為 eil101(有 101 個城市)。代碼使用 python 語言編寫,因此運算速度因為語言特性比編程語言要低。
旅行商問題,即 TSP 問題(Traveling Salesman Problem),是求最短路徑的問題,即“已給一個 n 個點的完全圖,每條邊都有一個長度,求總長度最短的經過每個頂點正好一次的封閉回路”。TSP 是組合優化問題,可以被證明具有 NPC 計算復雜性。如果希望暴力搜索其最佳解,其復雜度將是 O(n!),其計算量隨著 n 的增加將輕易超過目前計算機的可能算力。因此我們需要用更智能的方法求解。
於是我們先考慮局部搜索算法。局部搜索算法是貪心算法,他往往往鄰域中最好的狀態搜索,因此容易進入局部最優結果,而無法跳出局部最優的區域。
第二部分使用模擬退火算法。模擬退火算法從某一較高初溫出發,伴隨溫度參數的不斷下降,結合概率突跳特性在解空間中隨機尋找目標函數的全局最優解,即在局部最優解能概率性地跳出並最終趨於全局最優。模擬退火算法比起局部搜索算法,賦予了一定跳出局部最優解的能力,但能否跳出局部最優解依然依賴隨機性。
首先使用兩種不同的局部搜索算法。
第一種選擇鄰域的方法是隨機交換兩個城市在序列中的順序。每次循環中產生的候選序列為城市數(以下用 Cs 表示)*10,並從中選擇一個最優的(距離最短的)作為下一步。
第二種選擇鄰域的方法是隨機交換三個城市在序列中的順序。每次循環中產生的候選序列為 Cs*10,並從中選擇一個最優的(距離最短的)作為下一步。
這兩種算法都按以下步驟實現:
錄入初始狀態,並打亂順序產生一組隨機狀態,從這組狀態(包括初始狀態)中選最佳的狀態作為起點;
Repeat:
產生一個集合 S
Repeat 10 * Cs times:
將當前狀態加入 S
產生 2 個(或 3 個)互不相同的、范圍為[1, 城市數-1]的隨機數以這 2 個(或 3 個)隨機數作為下標交換城市在序列中的順序將交換後的序列加入 S 中從 S 中選擇一個最優的序列,作為當前狀態如果當前狀態與之前狀態一樣,則跳出循環。
可以知道,當當前狀態與鄰域中最佳狀態一樣時跳出循環,可以理解成到達局部最優解。雖然實際上這個鄰域並沒有完全覆蓋當前狀態的所有鄰居,但覆蓋全部鄰居需要(Cs-1) * (Cs-2)(第二種鄰域為(Cs-1) * (Cs-2) * (Cs-3))個數據,將加大每次循環的耗時,而且最終結果同樣是會進入局部最優結果而無法跳出。
第二部分在 LS 的基礎上加入 SA。
一開始我的 SA 流程如下:
得到初始狀態,設定初溫 T,降溫方式,結束條件外循環:
當符合結束條件則跳出循環內循環:
令當前解能量為 D0
通過鄰域搜索策略得到一組解並取其中最優(不包括當前狀態)解能量為 D1
令 ΔE = D1–D0
If ΔE <= 0: 則使 P = 1
Else: 使 P 為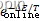
(或其他形式,其 P 應隨著 T 降低而降低,而且 ΔE 越小則越高)。
產生一個[0,1)的小數 R,若 R<P 則接受新狀態,否則不接受。
降溫
而本次實驗使用了非傳統的 SA——DSA-CE&MAP[1]

(以上為 DSA-CE&MAP 論文中描述的過程)
使用該種策略能在經典 SA 的基礎上更合理的降溫且更合理的得到選擇概率。
觀察概率函數可以發現,新解不僅與當前解比較,還與最佳解比較。用到概率函數的前提是當前解比新解好。當新解與當前解差距大的時候,分子會減小,P 減小,符合策略。當新解與最優解差距大的時候(注意這裡是最優解 – 新解),分母會增大,P 減小,符合策略。即,一個新解不僅考慮與當前解的差距,還考慮與曾到達的最優解的差距。這樣每次升溫將考慮到更多因素,使每次升溫更慎重。
這裡還引入了一個新的參數 coolingEnhancer 來影響降溫策略。當城市越多的時候,因為每個狀態將更復雜,引入 coolingEnhancer 使其降溫速度更慢,使外循環迭代次數增加,增強算法的適應能力。
在 DSA-CE&MAP 的基礎上,鄰域搜索策略我再作了修正,由於前兩種局部搜索策略效果不佳,使用了第三種局部搜索策略(2-OPT):
若 W(I, I+1) + W(J, J+1) > W(I, J) + W(I+1, J+1)則用邊(I,J)和(I+1,J+1)替換(I,I+1),(J,J+1)
其中 I,J 為某兩座城市的下標,W(a,b)表示城市 a 到下一座城市 b 的距離。這種策略能很好的解決路線交叉的問題,而上面兩種交換城市的方法很難處理路線交叉。這種方法可以理解成用凸四邊形的兩條對邊代替兩條對角線(好的效果)。
這種邊的替代依賴於該問題中城市之間的距離是對稱的(即交換兩個序列中相鄰的城市的順序不會影響兩城市之間的距離)。
假設原本的順序是 i,i+1,s[n],j,j+1,則邊替換後則變成 i,j,s[n].r,i+1,j+1,其中 i+1 與 j 之間的路線將會因為先到達 j 再到達 i+1 而反轉。我們觀察可以發現 i 和 j+1 是沒有變動的。S2 = (i+1) + s[n] + (j)是整個反轉了。因此我們只需要獲得兩個隨機下標並將其中的城市序列反轉即可得到新狀態。
用與其他搜索同樣的方法得到一個關於序列的集合,並挑最優解。
由於 DSA-CE&MAP 中給出的初溫過高,因此將初溫降低為 1000,並將結束條件設置為 T<1(試運行發現 T<1 後基本到達局部最優解),以進一步提升速率。
在結合 DSA-CE&MAP(改良模擬退火)與 2-OPT(局部搜索)後,達到了實驗目標的 10%。
測例:eil101,最優解 629
初始狀態:
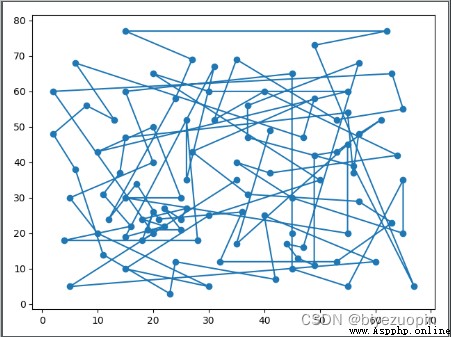
在使用 T = 1000,鄰域大小為 10,降溫速率為 0.001 時得到的一個最優解:
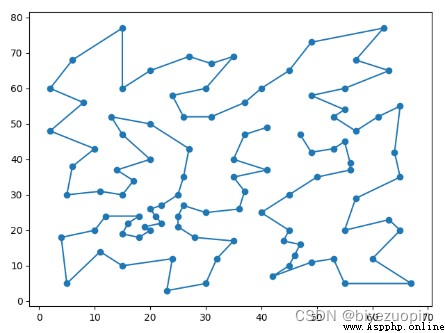
可以看到最優解已經沒有交叉路線(這是 2-OPT 的功勞,實際上即使沒有模擬退火,只有 2-OPT 也能輕易達到沒有交叉路線的結果),而且路線盡可能的圓潤。
運行環境為 windows10,Intel Core i5-8400 2.81GHz,RAM 2667MHz 16GB
編譯器 PyCharm,語言 Python3
以下為不同參數下的運行結果:
以下為不同策略得到的結果,每組測試 10 次。
其中策略一為交換兩個城市,策略二為交換三個城市,策略三為 2-OPT(部分逆轉)T 為初溫,Range 為內循環中鄰域大小(樣本個數),Coolrate 為降溫速率。
可以看到 2-OPT 的比起單純交換城市有好很多的效果。而對比模擬退火,能看到當溫度減少或鄰域范圍減小,最終解都會變差。但是減少初溫或減少內循環的鄰域大小能明顯減少時間消耗,其中第一行是第三行(模擬退火內)的時間的兩倍,而 Excess 相差僅 1%。
其中選取了一個數據如下的樣本
END Distance: 672.5236373155444
Times: 92102
Excess: 6.92%
totally cost 150.7281141281128 s
其中 T 的曲線如圖:
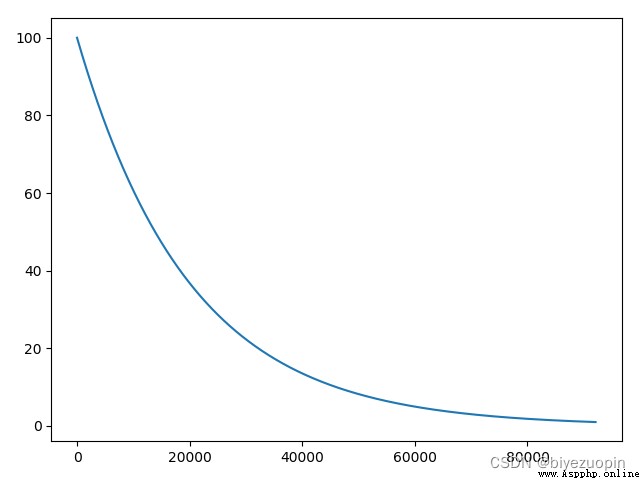
而每次外循環迭代時狀態的距離如圖:
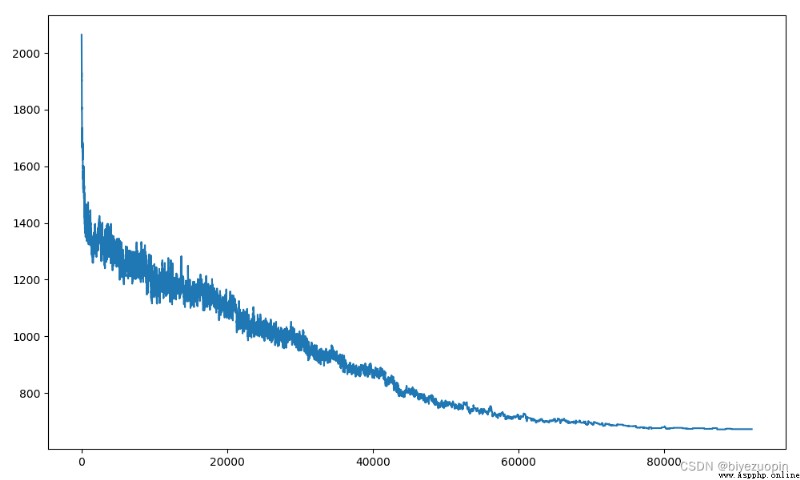
可以看到溫度的下降是非線性且平穩的單調遞減的,而狀態的值則有起伏,在越早期欺負越多,越到後期則越趨於平穩,這都是符合 SA 的規律的算法中其實還可以加入類似升溫、更好初始解等方法提高最終解的質量,但是升溫會顯著延長搜索時間。若升溫條件苛刻,則每次升溫前置時間過長;若升溫條件簡易,則容易頻繁升溫難以收斂。升溫的程度也是需要調試的部分。